一道圓錐曲線模考題的再思考和拓展

安徽省合肥市第一中學(xué) (230601) 谷留明

文[1]中筆者對合肥2019屆高三第一次教學(xué)質(zhì)量檢測數(shù)學(xué)(理)第20題進(jìn)行了研究，得到一些教學(xué)啟示.此后，筆者經(jīng)進(jìn)一步思考,對文[1]中的部分研究有了新的方法，得到本文中的一些拓展結(jié)論.

1 問題再現(xiàn)

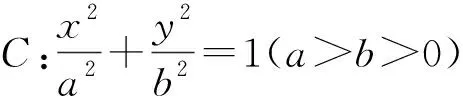
文[1]中，筆者分析了命題人所給參考答案的突兀性，并給出了另外兩種較為自然的方法,既然至少有這兩種較為自然的解法,那么參考答案里怎么會(huì)想到先證OM⊥ON?為何把這種方法作為參考思路?有無其它解法?背后有何“蹊蹺”?所以，筆者文[1]中對該考題，用參數(shù)方程的方法進(jìn)行了變式研究.這里用更為常用的解析法再次進(jìn)行研究.

先給出原考題的常規(guī)解析法.

這個(gè)解法直譯直敘,簡單自然,可以說是基本方法.雖然運(yùn)算量稍大一些,但這正是圓錐曲線解答題的特點(diǎn),數(shù)學(xué)運(yùn)算也是數(shù)學(xué)六大核心素養(yǎng)之一.

2 變式研究的新方法

變式1 圓O改為x2+y2=1,其它條件不變.試判斷|PM|·|PN|是否為定值.

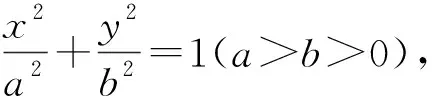
3 結(jié)論拓展

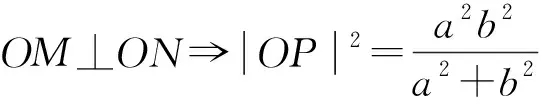
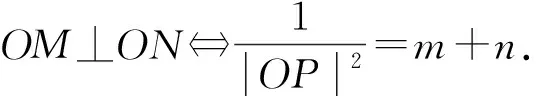
證明:設(shè)M(x1，y1),N(x2，y2).

由這些結(jié)論,命制類似的題目也就不足為奇了,參考答案的思路也就有了根據(jù).但是這些結(jié)論并非課程所要求的必須掌握的基本定理,選方法三作為參考答案很是不妥.筆者在講評這道題時(shí),結(jié)合自己的心得,逐步引導(dǎo)學(xué)生去思考,激發(fā)學(xué)生的鉆研精神,突出了對邏輯推理、數(shù)學(xué)運(yùn)算、數(shù)學(xué)抽象這三大數(shù)學(xué)核心素養(yǎng)的培養(yǎng).

4 問題引申

結(jié)論3 拋物線y2=2px(p>0)上有兩點(diǎn)M，N,O為頂點(diǎn),OM⊥ON,OP⊥MN于P,則lMN過定點(diǎn)Q(2p,0),且點(diǎn)P的軌跡是以線段OQ為直徑的圓x2+y2=p2(除原點(diǎn)O外).

評注：此結(jié)論中軌跡雖然也是圓,但證明方法與圓的位置等顯然與結(jié)論2有所區(qū)別.一方面結(jié)論2中,張直角弦所對的點(diǎn)O是有心圓錐曲線的對稱中心,而拋物線不是有心圓錐曲線,結(jié)論3中點(diǎn)O是拋物線的頂點(diǎn).另外,結(jié)論3中得到lMN過定點(diǎn).那么,在有心圓錐曲線中,頂點(diǎn)張直角弦所在直線是否過定點(diǎn),以及頂點(diǎn)在此直線上的射影的軌跡是什么？以左頂點(diǎn)為例,得到以下結(jié)論.

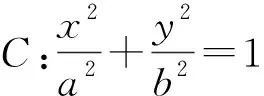
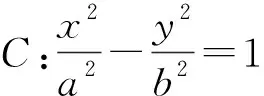
圓中的相關(guān)結(jié)論比較簡單,這里不做贅述.另外,還可以探討圓錐曲線的焦點(diǎn)張直角弦所在直線有何結(jié)論.