一道四點共圓問題的多解及其命題背景探究

南京師范大學附屬揚子中學 (210048) 郝結紅

江蘇省南京市溧水區教育局教研室 (211200) 魏國兵

1 模考試題呈現

(南京市2021屆高三年級第二次模擬考試第21題)已知直線l：y=x+m交拋物線C：y2=4x于A，B兩點.(1)略；(2)如圖1，若點M，N在拋物線C上，且關于直線l對稱，求證：A，B，M，N四點共圓.

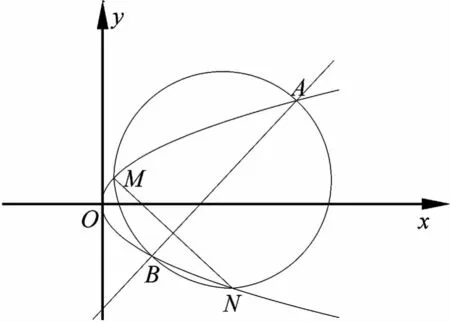
圖1

2 學生解法匯總

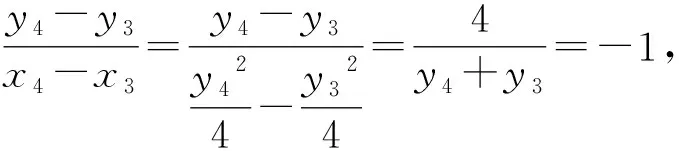
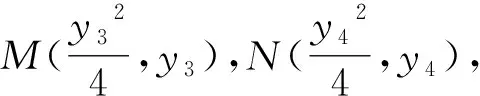
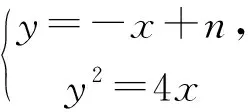
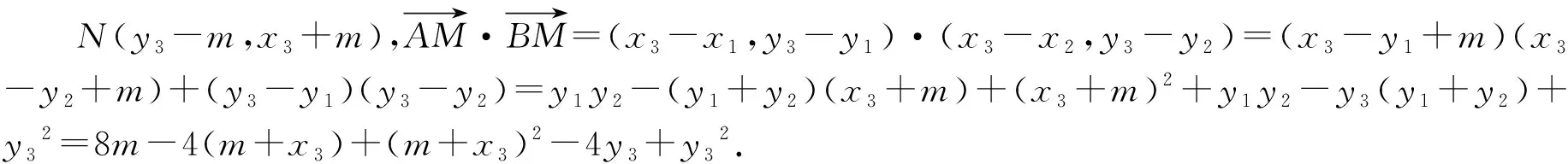
評析：以上4種解法本質是相同的：一是將四點共圓這個幾何問題，轉化為向量數量積為0這個代數問題；二是都是通過設坐標，利用斜率關系和中點關系，將題目條件進行坐標轉化和坐標消元.所以說：在解析幾何中，幾何指揮代數，代數為幾何服務，化歸坐標永遠是王道.

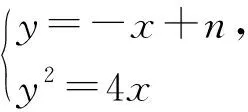
評析：利用與圓心和半徑解決四點共圓問題，也是一種好思路，用m表示半徑，用n表示半徑，還需要尋找兩者的關系n+m=-4進行消元.

解法6：(曲線系方程法)因為點M,N在拋物線C上，且關于直線l對稱，所以可設直線MN：x+y+n=0，由A，B，M，N滿足方程x-y+mx+y+n+2y2-4x=0，即x2+y2+(m+n-8)x+(m-n)y+mn=0，所以A，B，M，N四點共圓.

評析：具有某種共同性質的所有曲線的集合，稱為一個曲線系，并用含有參數的方程表示.此解法中，過兩直線L1：A1x+B1y+C1=0，L2：A2x+B2y+C2=0與二次曲線F(x，y)=0交點的曲線系方程為λL1L2+μF(x，y)=0.巧妙利用曲線系方程，大大降低了運算難度.

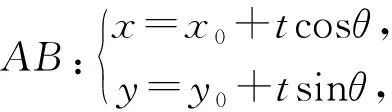
評析：巧妙利用直線的參數方程，也降低了運算難度.

3 命題背景探究

探究1 改變原題中拋物線方程，四點共圓仍然成立.

探究2 改變原題中直線l的斜率，四點共圓不成立.

探究3 將原題中拋物線方程改為橢圓方程，四點共圓仍然成立.

(1)證明：點P在C上；(2)設點P關于點O的對稱點為Q，證明：A、P、B、Q四點在同一圓上.

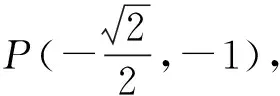
評析：此題揭示兩條斜率之和為0的直線與橢圓相交所得的四點共圓.

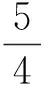
簡解：(1)易得C的方程為y2=4x；

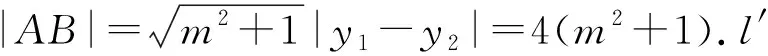
評析：此題揭示拋物線上四點共圓是有條件的.

圓錐曲線四點共圓定理若兩條直線y=kix+bi(i=1，2)與圓錐曲線ax2+by2+cx+dy+e=0(a≠b)有四個交點，則四個交點共圓的充要條件是k1+k2=0.

證明：兩直線組成的曲線方程為(k1x-y+b1)·(k2x-y+b2)=0，則過四個交點的曲線方程可設為(k1x-y+b1)(k2x-y+b2)+λ(ax2+by2+cx+dy+e)=0①.

(必要性)若四點共圓，則方程①表示圓，那么①式左邊展開式中xy項的系數為零，即有k1+k2=0.

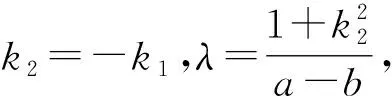
方程②的幾何意義是如下三種情形之一：表示一個圓、表示一個點、無軌跡.由題設知四個交點在方程②所表示的曲線上，故方程②表示圓.

評析：上述定理用文字表述，即斜率均存在的兩條直線與圓錐曲線(圓除外)有四個交點，則四個交點共圓的充分條件是兩直線的斜率互為相反數.這是一個非常簡潔的充要條件，運用這個定理可解決圓錐曲線上四點共圓的高考難題和數學問題.