基于教材習題的深度教學實踐與反思

廣東省佛山市順德區容山中學 (528303) 潘敬貞

廣東省東莞市麻涌中學 (523000) 駱妃景

1 引言

眾所周知，教材是課程標準的載體，是教材編寫者的集體智慧，也是師生教學的主要材料.從歷年高考試卷分析看，很多高考試題都是從教材習題改編、綜合、延伸、拓展、嫁接而來，具體表現為教材習題的數據的變更，條件的拓展，背景的變換以及結論的應用.因此，在平時的教學和高三復習過程中，一定要重視教材，尤其要重視對教材中經典題目的深入研究，本文對教材一道習題進行分析、變式探究以及類比拓展來激活教材習題，試圖構建深度教學與同行交流.

2 案例描述

2.1 片段一：問題呈現，挖掘設問

問題(人教版選修2-1第73頁習題6)直線y=x-2與拋物線y2=2x相交于A，B兩點，求證：OA⊥OB.

師：同學們，大家來看一下這個問題.(過了片刻)

師：哪位同學來說一下自己的想法？(在老師的引導下讓學生有充分表達自己想法的機會)

生1：我想將問題轉化為直線斜率進行證明，即證明kOA·kOB=-1.

師：非常好！這位同學是從直線斜率角度對該問題進行證明，其他同學還有不同的想法嗎？

師：非常好！這位同學是想利用向量工具進行求證，平面向量是解決平面解析幾何的重要工具.

師：這兩位同學都是想將幾何問題轉化為代數，利用代數方法解決幾何問題，其中關鍵問題是什么？

生3：最關鍵是坐標化，即聯立直線方程與拋物線方程求交點坐標.

師：大家動手試試.(大概過了2-3分鐘)

師：哪位同學展示一下.

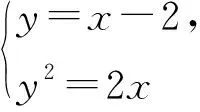
師：還有其它解法嗎？

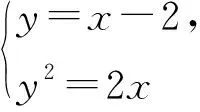
師：如果聯立直線與曲線方程消元后得到的一元二次方程容易求解的，求兩點的坐標也不失為好選擇，關鍵在于選擇合適方法，優化運算，簡化解題過程，提高解題效率.

師：請大家思考，根據已有的解題經驗，本題中的“OA⊥OB”還可以怎么處理？

此時給足學生回憶與聯想，最終師生共同歸納出：

變形2 以AB為直徑的圓經過坐標原點O.

變形4 設A，B的中點為M，且OM⊥AB，OM2=AM·BM.

設計意圖:高三后階段復習中，回歸教材，設計低起點的課本習題，旨在激勵更多的學生參與課堂活動，實現一題多解；問題變形處理環節意在聯系平面幾何知識溝通平面向量工具，構建知識體系，拓展學生的思維，提高學生轉化與化歸能力.

2.2 片段二：問題驅動，一題多變

變式1 若直線y=3(x-2)與拋物線y2=2x相交于A，B兩點，試問：OA⊥OB？

師：大家動手試一下.(過了幾分鐘)

師：哪位同學來展示一下.

師：這位同學做的非常漂亮，主要用向量工具和韋達定理，思路清晰，過程簡潔，大家掌聲鼓勵！(此時教室響起了熱烈的掌聲！)

變式2 若直線AB過點(2,0)且與拋物線y2=2x相交于A，B兩點，試問：OA⊥OB？

師：大家動手試試這道題.(幾分鐘后)

師：哪位同學來展示一下.

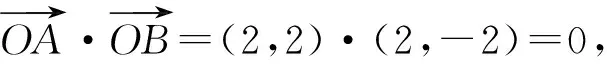
師：非常棒，這位同學思維嚴謹，他在設直線的點斜式方程時很細心，先考慮直線斜率不存在的情況，這是很多同學容易遺漏的.

設計意圖：改變源問題的條件，由特殊到一般進行變式探究，一方面鞏固源問題中涉及到的數學方法，培養學生大膽猜想，小心求證的數學品質，另一方面，也為得到一般結論做鋪墊.

教師通過投影展示不同學生的解答情況，并對學生解答中存在的“亮點”和“不足”作出必要的點評.

師：本題求解過程中存在幾點不足：一是有學生在設直線方程時用點斜式方程，遺漏了直線斜率不存在的情形；二是y1y2是通過k(x1-2)(x2-2)=kx1x2-2k(x1+x2)+4k增加了計算量.

師：大家反思總結以上幾道試題，大膽猜想有沒有什么發現.

生7：直線過定點(2,0)時，滿足OA⊥OB.

師：非常棒！問題反過來是否也成立呢？大家看一下變式3.

變式3 若A，B是拋物線y2=2x上異于頂點O的兩動點，且滿足OA⊥OB，試問：AB恒過定點嗎？

師：大家嘗試一下.(幾分鐘后)

師：誰愿意來展示一下？

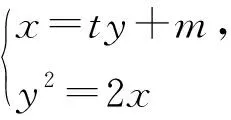
師：很好，請大家再觀察一下定點(2,0)與拋物線的方程y2=2x有什么關系呢？

生9：定點(2,0)中的橫坐標，恰巧是拋物線的方程y2=2x中的2p.然后我們小組進行了猜想如下：已知A，B是拋物線y2=2px(p>0)上異于定點O的兩動點，滿足OA⊥OB，直線AB恒過定點(2p,0).

師：完成的非常漂亮！那么我們現在是否可以初步下這樣的結論：“當滿足OA⊥OB時直線AB恒過定點”.

設計意圖：通過對課本習題的多角度探索，得到解決這一類問題的通法，同時注重方法的提煉與優選，滲透特殊值法、轉化的思想，也為得到一般結論做鋪墊.

2.3 片段三：一般推廣，一深化理解

變式4 已知A，B是拋物線y2=2px(p>0)上異于定點O的兩動點，滿足OA⊥OB，證明：直線AB恒過定點(2p,0).

師：哪位同學來展示一下.

師：真棒！如果將變式4的條件與設問調換是否同樣成立呢？大家動手探索一下.

變式5 已知A，B是拋物線y2=2px(p>0)上異于定點O的兩動點，若直線AB恒過定點(2p,0)，證明：OA⊥OB.

師：哪位同學來展示一下.

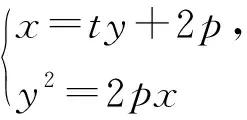
設計意圖：通過發散思考，把具體的拋物線得到結論推廣到一般情況，加深理解.

師：如果把拋物線上特殊定點O改為一般的定點結果將會怎么樣呢？大家請看變式6.

2.4 片段四：類比遷移，拓展延伸

變式6 過拋物線y2=2x上的點M(2,2)，作直線MA⊥MB交拋物線于A，B兩點，是否存在直線AB恒過定點，若存在，請求出該定點，若不存在請說明理由.

學生用上述解題方法和經驗，解出定點為(4,-2)，教師鼓勵學生大膽猜想，然后求證.

師：誰來展示？

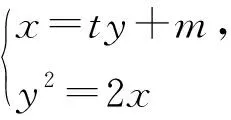
師：非常好！大家探索一下是否存在更一般化的結論，大家試求證一下變式7.

變式7 過拋物線y2=2px(p>0)上的一點M(x0,y0)作兩條互相垂直的直線與拋物線交于A，B兩點，如圖1.證明：直線AB經過定點N(x0+2p,-y0).

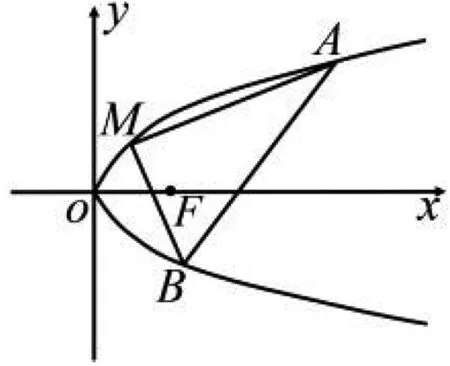
圖1

師：哪位同學來展示一下？

師：太棒了！還有其它解法嗎？

師：這兩位同學非常優秀！這樣我們得到這樣的結論：“過拋物線y2=2px(p>0)上的一點M(x0,y0)作兩條互相垂直的直線與拋物線交于A，B兩點，直線AB經過定點N(x0+2p,-y0)”.

設計意圖：從具體到一般，從拋物線頂點的特殊位置到一般位置，這樣由淺入深，由表及里，搞清楚了該類直線恒過定點的性質，使知識體系化.同時變式6讓學生進一步熟悉直線恒過定點的開放性問法.

2.5 鏈接課本和高考

鏈接1 (選修4-4第33頁例3探究)在例3中(O是直角坐標原點，A，B是拋物線y2=2px(p>0)上異于頂點的兩動點，且OA⊥OB)，點A，B在什么位置時，△AOB的面積最小？最小值是多少？

采用今天方法的解答，過程如下:

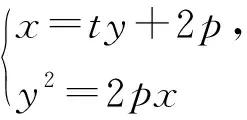
鏈接2 (2017年全國3卷理科20題)已知拋物線C:y2=2x，過點(2,0)的直線l交C于A，B兩點，圓M是以線段AB為直徑的圓.

(1)證明：坐標原點O在圓M上；

(2)設圓M過點P(4,-2)，求直線l與圓M的方程.

設計意圖：把分散在課本中例題、習題、高考真題聚結串聯起來，形成知識鏈，加深對一類問題的深刻理解，并且通過對課本題源的挖掘、引申、拓展，展現高考題的命題過程和思路軌跡，讓學生看到教材上例題、習題與高考題之間的內在聯系，消除了學生對高考試題的恐懼感和神秘感，同時幫助學生構建知識，掌握方法.

3 教學反思

3.1 后期備考思考

高三后階段復習，要回歸基礎、回歸教材，設計低起點的課本習題為切入點，旨在激勵更多的學生參與課堂活動，營造良好的學習氛圍，為后續的課堂教學做好鋪墊.然后通過溫和的變式，變式之間思維跨度不宜過大，綜合度不宜過高.一般從特殊情形出發，逐漸改變某些量得到一連串相關的變式題，最后觸及問題的內核，構建深度教學，引領學生深度學習.在此過程中，加深學生對數學“四基”的理解與掌握，提升數學“四能”發展數學素養.

3.2 復習教學要重視“導”

本節課所選的教材習題并沒有直接提到直線定點問題，但通過教師的引導將學生目光聚焦本節課的核心問題.教師科學的設計教學環節，通過改變定直線的斜率、過定點到一般直線，從特定曲線到一般曲線，從曲線上的特殊點到一般點學生經歷了從特殊到一般的研究過程，爾后教師引導學生分析：問題在變式過程中弄清變化的因子和不變的本質，從而得到一般的結論，再到鏈接課本和高考，讓學生體會發現問題，探究新知，應用知識解決問題的愉快過程.教學過程由淺入深、層層遞進，符合學生的元認知水平，提高學生參與課堂活動的積極性，又通過問題驅動為教學開展注入了活力，整個教學過程教師很好的做到了教師是主導學生是主體的課堂角色，教學效果顯著.

3.3 挖掘教材例題、習題

高三數學復習教學沒有教材，可以根據所教學生的認知特點以及心理規律和學生當前的數學基礎與數學能力等實際情況，全面研究課標、研究考綱、研究考題、研究教材例題，有機整合教材例題、習題.在尊重教材例題、習題的基礎上，對教材例題、習題進行推廣、變式、類比探究、改編等方式方法激活教材例題、習題，編寫復習材料.可以將教材例題、習題原先主要用來鞏固知識、深化概念理解的知識立意改編成突出能力立意，突出數學思想方法的學習；可將教材例題習題的單純解答問題改編成突出回顧復習知識，建構知識體系，鞏固知識結構；可將教材例題、習題“結構良好”的封閉題改編成“思維發散”的開放題，如：探究型存在性問題、探索性問題、歸納猜想和演繹證明等問題，創造性的使用教材例題、習題，讓教材例題、習題更好地發揮其教學作用.