促進自然生成 凸顯數學本質
——以“三角函數的概念”教學為例

浙江省湖州市濱湖高級中學 (313000) 鄭夢華

浙江省湖州中學 (313000) 祝峰澤

數學教育基本理念是“以學生發展為本，立德樹人、提升學生核心素養，培養學生的科學精神和創新意識，實現不同的學生得到不同的發展，培養具有終身學習能力并適應社會需要的人才”，數學本質實際上是指數學知識的內在聯系、數學規律的形成過程、數學思想方法的提煉以及數學理性精神的體驗，教師通過問題驅動引導學生在課堂中通過活動探究分析、解決問題，學生在活動探究過程中，通過親身體驗數學知識的形成過程，體會到數學知識的理性精神與科學精神，并在知識的探索過程中逐步摸索其中蘊含的數學思想方法、數學研究工具，掌握并理解數學本質，提高學生終身學習能力，最終實現學生個人的發展.因此，數學教學中通過問題驅動讓學生知識自然生成中掌握數學本質不失為一個有效又合理的教學方法，該教學模式也能為當下數學教育改革尋找一個新路徑.

筆者對“三角函數的概念(人教A版2019)”一課進行課堂實錄，節選部分教學片段進行分析評價，教學過程中主要通過問題驅動引導學生進行活動探究、獨立思考等讓學生在課堂中掌握理解三角函數概念的數學本質，體會其中蘊含的數學思想方法、數學規律，體驗數學知識的生成過程及數學的理性精神，加深學生對三角函數的概念的理解，培養學生的學習能力，從而實現學生的素養發展.

1 課堂實錄(節選片段)

1.1 在活動中提煉數學思想方法

提出問題：讓學生以三人一組為單位，組號記為A、B、C等，每一組任意畫一個銳角，記作角α、β、γ等，借助三角板，各自求出該銳角的正弦值、余弦值和正切值的近似值.

學生回答如下表：(投影儀展示，此略)

師生活動：師生一起了解三角函數的數學史，了解數學史中三角函數定義——線段比.

設計意圖：讓學生對不同的銳角以及同一個銳角運用不同的線段比去計算三角函數值，從一般的銳角三角函數值計算中體會到其線段比的數學本質定義，及數學史的角度.學生能夠從中體會到相同的定義，提煉了從一般到特殊的思想方法，為學生后續運用數學思想方法進行學習打下深厚的基礎.并且學生是在自己的活動經驗中進行體會，學生對數學思想方法的理解和運用能夠更加深刻.

1.2 在思考中體會數學規律

提出問題：大家所求的銳角三角函數值有何特點呢？

學生回答：角的大小確定時，對應的銳角三角函數值差不多相等，為該角所在的直角三角形中線段長度的比值.

提出問題：與你們找的點所在的位置有關嗎？

學生回答：無關.

提出問題：既然銳角三角函數值與點A所在的位置無關，那你們能否找到一個點A，使銳角三角函數值計算更簡潔呢？

設計意圖：這一過程教師是通過三個問題引導學生思考，有何特點、是否有關、如何更簡潔等問題，通過一連串精簡的提問，給學生充足的思考時間讓學生發現任意的銳角三角函數值的共同特征是線段比這一數學規律，以及三角函數中可以運用單位圓這一研究工具使問題更簡便，學生在自己的獨立思考之中領悟數學知識中蘊含的數學規律，學生能夠對規律的形成以及理解更深刻，后續的使用也能更得心應手，同時學生在思考過程中的體驗都能給學生后續學習提供一些幫助.

1.3 在已有的數學現實上建構新知

提出問題：既然銳角三角函數值sinα只與角α有關，那么sinα和角α有什么關系呢？

學生回答：(生1)三角關系；(生2) 函數關系.

提出問題：α是一個數嗎？

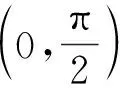
設計意圖：高中數學由代數、幾何、統計與概率幾個模塊內容展開，而函數是代數的一個重要主線，三角函數又是函數的一個重要分支，如何將銳角三角函數值過渡到三角函數，讓學生能夠從函數的角度研究三角函數值，這對于學生來說是一個質的變化，在這一過程，教師通過提問式，讓學生對自己的回答與他人的回答進行反思，并在反思與猜想中與自己已有的數學現實進行聯系，對已有的知識系統進行重新建構，發現在角度與銳角三角函數值之間也有一種特殊的關系，而這種特殊的關系正符合函數的定義，在這一過程中，學生是自己通過猜想論證過程得到三角函數的函數本質，而不是教師直接告知學生銳角三角函數也是一個函數的，學生能夠通過對自己知識系統進行聯想，再創造發現銳角三角函數的函數本質，這種學習方式也能為學生后續學習三角函數的概念、性質等奠定基礎.

1.4 運用數學工具得到數學概念

提出問題：既然sinα是一個函數，自變量是銳角α，那如果角α為其他角度時，是怎樣的呢？

學生回答：(生1) 在平面直角坐標系作角(弧度制是在平面直角坐標系中研究得到)；(生2)隨便作一個角.

提出問題：如果角α為其他任意角時，此時角α與sinα的定義是怎樣的？

師生活動：學生利用已有經驗作任意角，教師則運用幾何畫板作可以轉動的任意角(以原點O為角的頂點，以x軸正半軸為角的一邊OB，轉動另一邊，表現任意角)，隨后學生之間進行交流探索，得到以下幾種不同結果.

學生回答(隨意作任意角)：運用直尺作直角三角形，度量長度得到三角函數值.

提出問題：你們覺得自己所作的角能清晰明了地表現三角函數值與角的關系嗎?如何作角才能簡潔明了地體現三角函數的特征？

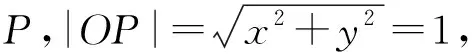
設計意圖：教師通過問題引導學生將銳角拓展到任意角，任意角如何表示及其三角函數如何定義是這一教學過程的重難點，首先讓學生自己作出任意角，教師用幾何畫板作角，此時學生作角有各種情況，但是當他們在求所作角的三角函數值時，學生發現三角函數值求解較復雜，此時讓學生進行對比討論，學生發現將直角三角形與平面直角坐標系、單位圓相結合時，運用單位圓及坐標能夠簡潔明了地表示出角的三角函數值，單位圓與平面直角坐標系的教學工具是學生自己發現的，由銳角到任意角，始終抓住三角函數原始定義線段比，運用單位圓，實現由幾何定義法——終邊定義法——單位圓定義法得到最簡潔的三角函數的定義，學生在這個過程能夠對三角函數的概念有一個深刻的理解和認識，并且始終是學生去尋找工具、發現概念，由此發揮了“以學生為主體”的教學思想，并且在三角函數的概念獲得的過程中凸顯了數學工具的重要性，也為學生后續學習選擇合適的數學工具、數學方法提供了一些經驗.

2 感悟結語

通過本節課的教學，我們認為數學本質是數學學習的核心，在數學教學中教師應瞄準學生如何“學”，讓知識不再是直接呈現給學生，而應讓學生參與到課堂，喚醒學生的思考能力，讓學生在探究思考的過程中能夠了解知識的生成過程，體會到數學學習的方法、工具，從而培養學生的學習能力.