卡爾曼濾波算法在隧道結構沉降分析降噪中的應用

王賓賓

(中鐵第一勘察設計院集團有限公司 軌道交通工程信息化國家重點實驗室， 西安 710043)

鐵路客運、貨運專線穿越高山峻嶺時需要穿越隧道，城市地鐵線路幾乎全程運行于隧道之中，而隨著我國軌道交通工程的迅速發展，隧道開挖里程日益增加。隧道結構的穩定性一直是人們關注的焦點，直接影響鐵路運行安全，隧道結構的變形監測與分析能夠及時發現安全隱患，有助于及時采取措施避免安全事故的發生[1-2]。

變形分析中常用的去噪方法有時間序列、灰色系統分析、BP神經網絡和卡爾曼濾波等[3-7]。卡爾曼濾波是一種動態系統分析方法，它將物體的運動過程用一組狀態微分方程和觀測方程描述，通過不斷預測與修正實現對動態運動過程的濾波和預測。卡爾曼濾波不需要存儲大量的歷史數據，可以跟隨觀測值邊觀測邊預測，處理效率高，因此在變形分析中得到了廣泛應用。卡爾曼濾波初值的選取對濾波過程影響較大，且狀態向量的隨機模型只能根據經驗得到，不合理的初值和隨機模型可能引起濾波發散。許國輝等[8]對濾波初值的選擇和模型的確定進行了探討，并通過實例證明了方法的有效性。方差補償自適應卡爾曼濾波可以利用剩余觀測值的預測殘差估計動態噪聲的方差并予以修正，可有效避免濾波發散。

1 經典卡爾曼濾波算法模型

卡爾曼濾波根據系統的時間特點可分為連續系統和離散系統[9]。隧道結構沉降監測是按照一定的時間間隔對監測點進行觀測，確定監測點的周期變化量，其處理過程是一個典型的離散線性系統濾波問題。

1.1 離散線性系統的數學模型

離散線性系統的數學模型由一個具有隨機初始狀態，并帶有動態噪聲的線性微分方程和離散觀測方程描述。離散線性系統的狀態方程和觀測方程為[10-12]：

(1)

式中：Xk、Xk-1為狀態向量，Ωk-1為動態噪聲，Lk為觀測值向量，Δk為觀測噪聲，Φk,k-1為狀態轉移矩陣，Γk,k-1為動態噪聲系數，Bk為觀測方程系數。

1.2 離散線性系統的卡爾曼濾波方程

設Ωk，Δk是零均值白噪聲，且兩者之間完全不相關，X0的先驗期望為(0/0)，方差為DX(0)，X0與Ωk、Δk不相關。按照廣義二乘原理，增加虛擬觀測值并逐次平差后可得卡爾曼濾波遞推方程為：

(2)

(3)

式(2)為一步預測公式，式(3)為修正公式。

2 方差補償自適應卡爾曼濾波算法模型

經典卡爾曼濾波由于數學模型不合理，動態噪聲和觀測噪聲的統計性質不準確，以及遞推過程中的舍入誤差影響，可能會導致狀態估計值偏離實際狀態越來越遠，出現濾波發散現象。常用的克服卡爾曼濾波發散的方法有漸消記憶法、限定記憶法、限定下界法和方差補償自適應卡爾曼濾波算法等。方差補償自適應卡爾曼濾波算法應用廣泛，該方法是在利用觀測數據進行濾波時，不斷對未知的或不確切的模型參數以及噪聲的統計性質進行估計和修正，減少模型誤差[11]208-212，215。

2.1 動態噪聲方差陣的估計

定義第l步預測的殘差Vk+l為：

Vk+l=Lk+l-k+l

(4)

式中：Vk+l為第l步預測的殘差，Lk+l為第k+l期觀測值，k+l為第k+l期最佳預測值，k+l=Bk+lΦk+l,kk，Vk+l服從正態分布N(0,Dvv)。

由式(4)可得Vk+l的方差Dvv為[13-15]：

(5)

假定DΩ(k+i-1)在第k期之后的N期時間段上為常量對角陣，即：

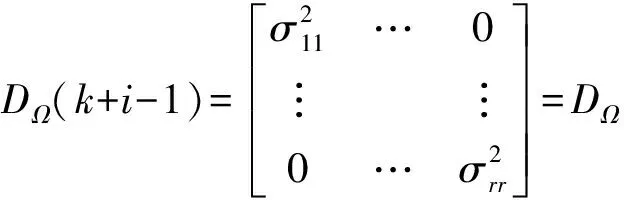
(i=1,…,l)

(6)

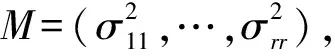
(7)

式(7)中：δk+l為零均值隨機變量，l=1,…,N。

令：

(8)

將式(7)代入式(8)并顧及式(5)可得：

(9)

此時，令：

(10)

由式(9)、式(10)可得：

Wk+l=C(k,k+l)MT+δk+l

(11)

以M作為參數，由式(11)可得誤差方程的一般形式：

(12)

即有：

(13)

按最小二乘原理，當N≥r時T有唯一解，組成法方程并求逆得M的估計值為：

(14)

式中：C=[C(k,k+1),…,C(k,k+N))]T，W=[Wk+1,…,Wk+N]T。

2.2 方差補償自適應卡爾曼濾波算法流程

方差補償自適應卡爾曼濾波在進行濾波時利用預測值和剩余觀測值估計動態噪聲的方差，并以動態噪聲方差估計值進行新的濾波，算法流程如圖1所示。

圖1 方差補償自適應卡爾曼濾波的算法流程Fig.1 Algorithm flow of variance compensation adaptive Kalman filter

3 應用實例

3.1 項目概況

廣州某新建高速鐵路站前工程，設計橋梁共9座，總長27.23 km；涵洞11座；隧道4座，總長4.92 km；區間路基共8段，總長1.26 km。按照相關規范要求，施工期間必須對沿線路基、涵洞、橋梁和隧道等進行動態沉降變形觀測，通過對沉降觀測數據進行綜合分析和評估，驗證和調整設計參數與措施，使路基、橋涵、隧道等線下工程達到規定的變形控制要求。本標段線下工程沉降變形觀測工作以橋涵、路基、隧道等建(構)筑物的垂直位移觀測為主。

3.2 布網方案

本項目隧道垂直位移監測要求采用沉降變形等級三等(國家二等水準測量)施測，根據沉降變形測量精度要求高的特點，以及標志的作用和要求不同，垂直位移監測網布設分為基準點網、工作基點網和沉降變形觀測網三級。

本項目要求觀測隧道的仰拱部分，隧道水準路線觀測按二等水準測量精度要求形成閉合或附合水準路線，沉降觀測點位布設于觀測斷面隧道仰拱頂面，圖2為附合水準路線示意，圖3為觀測點位埋設示意。

圖2 附合水準路線示意Fig.2 Diagram ofannexed leveling line

圖3 觀測點位埋設Fig.3 Diagram of points buried

3.3 濾波分析

以該項目中隧道閉合水準線路L93764為例，線路起閉于JM237點，共觀測18個點，其中JM237和JMX- 4為工作基點不計算沉降量，中間設置16個監測點，觀測方案見表1，該線路觀測頻率為1次/5天，共觀測26期數據。

表1 L93764水準線路觀測方案

以087440S2點的26期數據為例，對文中方法進行可行性和有效性的驗證與分析，原始沉降數據見表2，表2中的首期數據不計算沉降量和沉降速率。

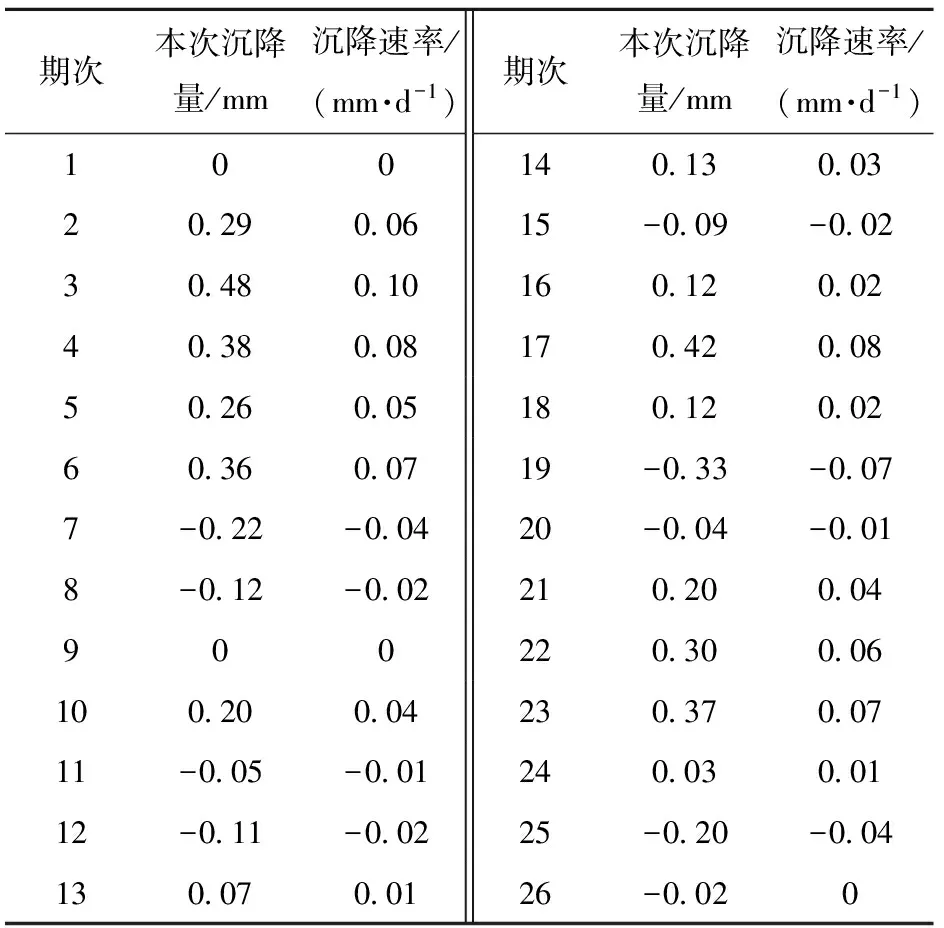
表2 087440S2原始沉降數據

選取該點前5期沉降量和沉降速率的平均值作為初值，分別利用經典卡爾曼濾波算法和方差補償自適應卡爾曼濾波算法進行分析，經過濾波后的沉降量如圖4所示，可以看出經卡爾曼濾波處理后的沉降量大大降低了測量噪聲，且隨著時間的推移，波動量逐漸變小并能更加合理地反映監測點的沉降趨勢。

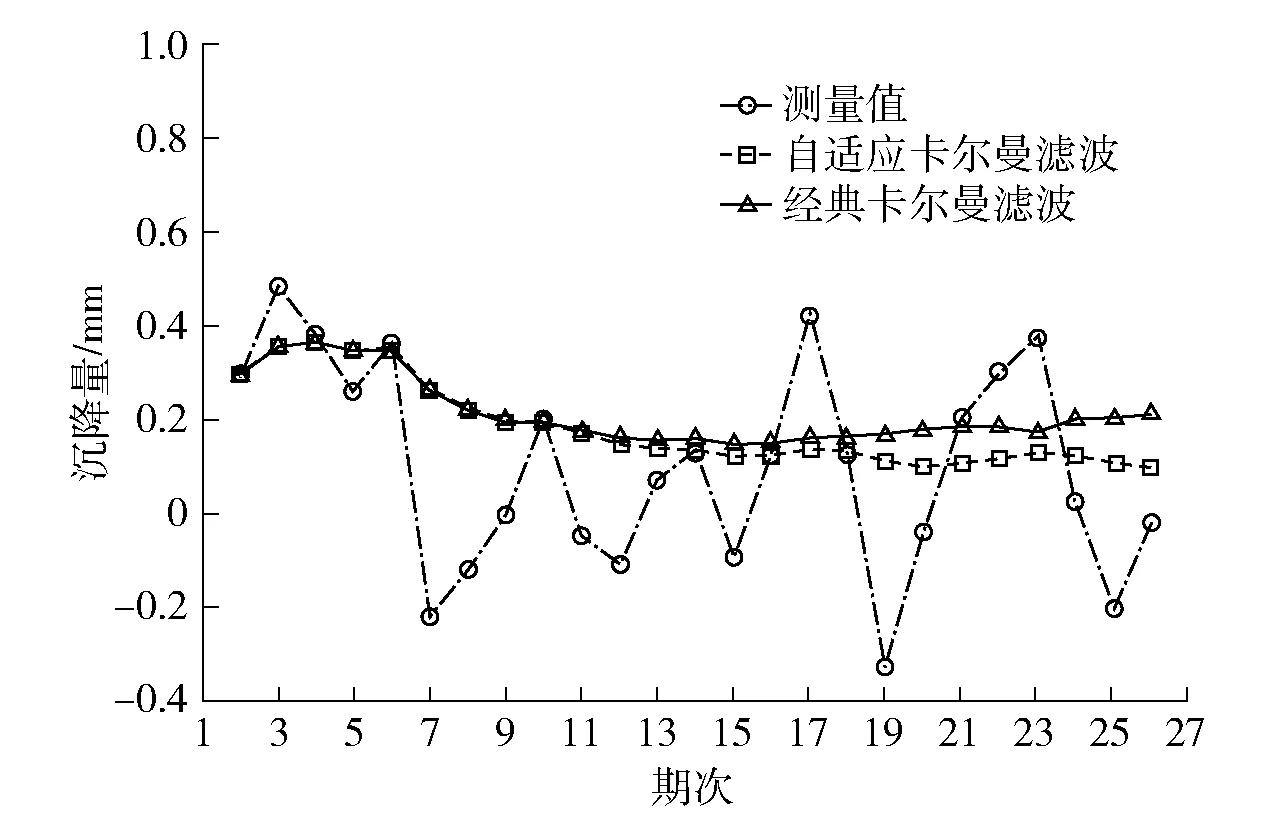
圖4 卡爾曼濾波結果Fig.4 Graph of Kalman filter results

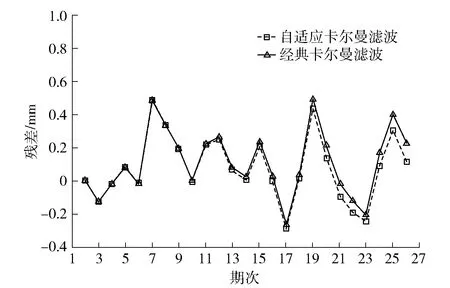
圖5 卡爾曼濾波殘差Fig.5 Graph of Kalman filter residual

4 結論

本文分別利用經典卡爾曼濾波算法和方差補償自適應卡爾曼濾波算法對隧道結構進行沉降分析，通過工程項目算例得出如下結論：

1)隧道結構的沉降測量中伴隨著各種測量噪聲，若直接利用原始測量值對監測點進行分析，在沉降量比較小、信噪比較低的情況下，測量噪聲對隧道結構的穩定性判定影響非常大，因此必須采用濾波方法降低測量噪聲。

2)卡爾曼濾波算法能夠有效減小沉降分析中的誤差影響，使測量數據能夠更加真實反映隧道結構的沉降趨勢。

3)方差補償自適應卡爾曼濾波算法在進行濾波時利用剩余的測量數據對動態噪聲方差進行預計和修正，濾波后的精度高于經典卡爾曼濾波，且不易受測量誤差的影響而發散。