例談課堂教學中發展學生個性化思維的策略

陸菲

[摘? 要] 在小學數學教學中，培養學生的個性化思維，可以促進學生的個性發展，實現教育的終極目標。然而由于一些“干擾因子”禁錮了學生個性化思維的發展，因此，文章從分析學生個性化思維發展的“干擾因子”著手，談談教學中的各種不完美，并給出發展學生個性化思維的教學建議。

[關鍵詞] 個性化思維;發展;小學數學

隨著基礎教育課程改革的不斷深入，“生命化”“創新性”和“個性化”等新型教育理念比比皆是，這些教育理念無一不充盈著生命活力和成熟魅力，倘若教師可以做到正確理解且合理利用，勢必可以讓學生的個性化思維綻放光彩，進而促進學生的健康成長和可持續發展。審視當下的課堂教學，或多或少地存在著大量干擾學生個性化思維發展的現象，禁錮了學生個性化思維的發展。作為一名教育一線的小學數學教師，筆者常常反思：是什么干擾了學生的個性化思維發展？該如何正確引導才能使學生展開個性化思維的翅膀，自由翱翔呢？

一、個性化思維發展的“干擾因子”

1. 動態課堂中教師的“主導”

新課程下的數學課堂是動態生成的，教師應從學生的需求和課堂學習的實際情況出發，擺正自身的位置因勢利導，以高超的課堂駕馭能力和豐富的教育智慧來隨時調整課堂教學，使學生的個性化思維得到張揚。而事實上，不少教師的教學水平一般、教學方式單一、教學方法不靈活，在課堂中習慣于“領導”課堂，反復強調“就是這么做的”，否定學生的思維偏差和個性想法，扼殺學生的個性化思維。

案例1? 認識分數

問題：請試著在長方形中以陰影表示 。

師：請大家試著在紙上畫一畫。

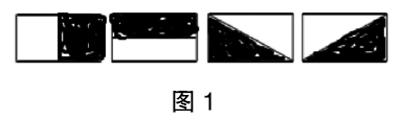
學生獨立完成，教師來回巡視。之后請幾名學生展示幾種正確答案（如圖1），并給予表揚。

生1（迫不及待地）：老師，看看我的畫法正確嗎？（如圖2）

師：不對。

分析：就這樣，由于教師的一口否定，極大地打擊了這名中等生的思維積極性。暫且不論這名學生思維是否正確，但教師這樣毫不留情地否決極大地抹殺了他的個性感悟，與此同時，也浪費了一次極好的可生成性資源。而事實上，該生僅僅是中心點沒有準確定位才造成了一些偏差，只需引導學生將所畫線段稍加調整，找尋到中心點，過中心點的任意線段都可以畫出這個正方形的 。（如圖3）

2. 問答中生生之間的思維干擾

課堂上，教師提問學生回答較為普遍，也盡顯自然。但大部分教師在問答間忽視提問細節，造成學生間思維干擾，找尋不到自身的個性體驗;或者過于關注學優生思維，忽視大多數學生表達個性化思維的主動性，從而使得大部分學生的思維“隨波逐流”，毫無個性可言。

案例2? 媽媽拿來16塊糖果，讓紅紅與她的7個好朋友平分，那么其中3個小朋友所分得的糖果占總數的幾分之幾？

師：哪位學生愿意說一說你的想法？

生1（自信十足地）：16塊糖果平均分給8個小朋友，每人分得2塊，三個小朋友可分得6塊，則6占16的 。

師：非常棒的想法！那就請你將答案在黑板上寫一寫，其他同學讀一讀。

……

這是筆者在一節示范課觀摩中所看到的教學過程，而當時坐在筆者旁邊的一位學生的本子上卻寫著這樣的解題過程：3÷8= ，而在聽到生1的解答后，他不假思索地擦去了自己的答案。事實上，這名學生的解題思維個性而簡潔，他直接通過分數之比求出分得的糖果占總數的幾分之幾。為什么他不僅不敢表達自身的想法，還否決了自身的答案呢？很顯然，這是一名中等生，他習慣于踩著別人思維的腳印前行，早已在不知不覺間喪失了自身的個性化思維。

二、發展個性化思維的方法

教師應該如何施教才能有效地發展學生的個性化思維？筆者有以下幾點建議。

1. 巧設氛圍，誘導求異意識

托爾斯泰曾說：“成功的教學需要的并非強制，而是興趣的激發。”興趣是個性化思維的源泉，是個性發展的動力，是創新的內驅力。所以，教師要精選例題，創設情境，讓學生充分經歷觀察、思考和創造的過程，誘導學生的求異意識，使其充分體會到探究的快樂，享受個性化思維求異活動帶來的幸福感。

案例3? 轉換的策略

問題：草地上一共有10只小雞和小兔在覓食，一共有32條腿，那么小雞有多少只？小兔呢？

一般方法：直接運用轉換策略。

求異策略：圖示法。

如圖4，首先畫出所有動物的頭，共10個，再一一畫上兩條腿，表示一共10只小雞，這樣就只有20條腿。接著，從第一只開始加兩條腿，則變成1只小兔，當加到第6只時已經達到32條腿了。從而得出小兔6只，小雞4只。

以上案例中，學生的求異思維并非教師發出的“指令”，而是學生內心自發的想法，這就是學生認可的思維求異的好機會。把握這樣的機會，需要教師替學生創造內需的氛圍，給足學生思考和創造的時間，“逼”學生思考并發現獨創性思路，并產生表達的愿望，進而逐步促成個性化思維。

2. 尊重個性，助力聯想思維

新課程的最高宗旨是“為每個學生的發展”施教的，因此教師要“以生為本”，樹立發展學生個性的思想。每個學生天賦各異，秉性不同，教師面對千差萬別的個體所組成的群體，需要放開手腳，放下姿態和身段，把學生看作發展的、獨特的、個性的個體，而并非隨意捏造的“泥土”，充分尊重學生的個性，為聯想思維助力，讓個性化思維百花齊放。

案例4? 長方形的周長

問題：已知長方形的長為10米，寬6米，試求長方形的周長。

師：哪位學生來展示一下你的解法呢？

生1：（10+6）×2=32（米）。

師：誰還能用其他方法求出它的周長呢？（學生張開聯想的翅膀，得出以下多種多樣的解法）

生2：10+10+6+6=32（米）。

生3：10+6+10+6=32（米）。

生4：10×2=20（米），6×2=12（米），20+12=32（米）。

……

教師在審視教學內容時需要擁有“高觀點”，而在面對學生時則需要“俯下身”。以上案例中，教師對學生的學習做出準確的預估，讓學生心目中的思路和方法可視化，助力學生的思考和聯想，從而有利于個性化思維這一關鍵能力的發展。

3. 鼓勵想象，呵護獨創思維

著名哲學家黑格爾曾說：“創造性思維需要豐富的想象。”想象可以激發獨特的思維成果。將大膽猜想引入數學教學中，可以活化思維，培養獨創思維，促進能力的提升。所以教師需鼓勵學生打開自由想象的閘門，勇于猜想、勤于猜想、善于猜想，培養獨創思維。

案例5? 周長是24厘米的長方形和正方形，哪個的面積更大？

師：你們猜想一下哪個面積大呢？

生1：正方形。

生2：我認為是長方形。（學生有的贊同生1的觀點，有的支持生2的結果，展開了火熱的辯論）

師：既然大家爭執不下，那該怎么辦呢？

生3：我們可以來驗證一下。

師：如何驗證呢？

生3（想了想）：我們可以用一個相同周長的長方形和正方形來試一試啊。

師：非常棒的想法！那就讓我們一起來驗證。你們看，老師手里有一些24厘米長的鐵絲，我們分成8個小組來探索，每個小組以表格的形式記載你們的實踐結果，并闡述你們的結論。（學生立刻投入操作過程，并填寫表1）

表1

師：現在可以說一說你們的結論了嗎？

生4：周長相等的情況下，正方形的面積大于長方形面積。

這就是數學課堂該設計的場景和氛圍，學生所思考和領悟到的知識更多來自實踐，使得學生的思維逐步完善;也就是在教師的鼓舞下，學生的獨創思維才能得以迸發;也正是因為經歷了這樣的曲折，所以收獲的結論才彌足珍貴。

總之，教師應該把學生個性化思維的培養當作數學教學的“行動指南”之一，著眼于學生的自身發展，擺平個性化思維發展的“干擾因子”，創設氛圍，尊重學生，給足學生經歷、探究和體驗的時間和機會，鼓勵學生想象，真正意義上放飛思維，促進個性化發展。