命題反思：警惕“喜好偏向”，擺正教學導向

周紅娟

摘要：從一份八年級的校級期末數學試卷中的一道考查配方法的閱讀理解題的解答與評分情況說起，反思其命題的教學導向及暴露出的“喜好偏向”，指出：命題需要警惕網絡流行試題和自身教研興趣成為“喜好偏向”，可以通過重視教材“經典問題”擺正教學導向。

關鍵詞：試題命制;教學導向;“喜好偏向”;配方法

最近，受學校教導處信任，筆者被安排命制一份八年級的校級期末數學試卷，測試范圍包括整式乘法與因式分解。由于多年任教九年級，筆者覺得，八年級這部分內容的教學要重視完全平方公式以及配方法，因為配方法在九年級一元二次方程、二次函數問題的解決中有著非常廣泛的應用。所以，命題組卷時，筆者選用了一道考查配方法的閱讀理解題。本文從該題的解答與評分情況說起，反思其命題的教學導向及暴露出的“喜好偏向”，提供研討。

一、一道配方法閱讀理解試題及其解答與評分

（一）試題

我們知道，利用完全平方公式可以將二次三項式a2±2ab+b2分解成（a±b）2。而對a2+2a-3這樣的二次三項式，則不能直接利用完全平方公式分解，但可以先用配方法配出一個完全平方式，再用平方差公式分解，過程如下：

a2+2a-3=a2+2a+1-1-3=（a+1）2-4=（a+1+2）（a+1-2）=（a+3）（a-1）。

請用配方法解決下列問題：

（1）分解因式：a2-6a+5;

（2）已知ab=34，a+2b=3，求a2-2ab+4b2的值;

（3）若4x2+12x+m分解因式所得結果中有一個因式為x+2，試求常數m的值。

（二）預設解答和評分

第（1）、第（2）問不算太難，筆者預設學生根據閱讀材料，利用完全平方公式能夠順利解決。對第（3）問，筆者預設的解答思路是：將多項式4x2+12x+m局部配方，可得[（2x）2+2×2x×3+32]-9+m=（2x+3）2-9+m;因為4x2+12x+m分解因式所得結果中有一個因式為x+2，即利用平方差公式對代數式（2x+3）2-9+m變形會產生因式2x+4，這樣就可逆向推導出（2x+3）2-9+m=（2x+3+1）（2x+3-1）;等式兩邊比較，得出-9+m=-1的結論，可得m=8的結果。為突出對配方法的考查，筆者預設評分標準：使用十字相乘法等其他方法得出正確結果的，得分減半。

（三）實際解答和評分

閱卷所見學生的解題思路很多。以下是閱卷組收集的一些學生的解法：

解法1根據多項式乘法法則（a+b）（c+d）=ac+ad+bc+bd，以及多項式乘法和因式分解之間的互逆關系，將多項式4x2+12x+m因式分解，得4x2+12x+m=（x+2）（4x+n），因而可得8+n=12，

m=2n，解得n=4，

m=8。

解法2對多項式4x2+12x+m局部變形，得4x2+12x+m=4x（x+2）+4x+m，分析得出4x+m這個多項式中含有x+2這個因式，即4x+m=4（x+2），進而求得m=8。

解法3畫出圖1，大矩形的面積是4x2+12x+m，被分成4個面積是x2的正方形和4個面積是2x的矩形，以及A和B兩個矩形。矩形A的一邊長為x，面積為12x-8x=4x，算出其相鄰的另一邊長是4，因此矩形B的面積是2×4=8，即m=8。

解法44x2+12x+m分解因式所得結果中有一個因式為x+2，說明方程4x2+12x+m=0有一根為x=-2。將x=-2代入方程4x2+12x+m=0，可得16-24+m=0，求得m=8。

解法1充分體現了“回到定義”的解題思想，即基于整式乘法與因式分解的互逆關系，設出另一個因式，求出待定的系數。解法2體現出對分組分解法的較好理解，即先在一部分和式中找到已知因式，得到剩下的和式中也有已知因式。解法3充分利用了二次式的幾何意義，借助矩形的拼接，以形助數直觀獲解。解法4從方程的視角看多項式，基于方程的根與多項式的因式的關系，靈活運用方程的根的概念，采用試根法解決問題，體現了“高觀點”的解題思想。

閱卷組覺得，這些解法各有各的精彩，各有各的價值，如果因為沒有采用配方法而被扣去較多的分，對學生而言是不公平的。于是，閱卷組討論決定修改評分標準：不使用配方法，而使用其他方法得出正確結果的，只扣1分——之所以還扣分，是因為題目提出了使用配方法的要求。

二、關于命題的“喜好偏向”及教學導向的思考

檢索一些搜題網站、組卷網站，可以找出海量的名校試卷、縣區期末試卷以及全國各地中考試卷。前兩類試卷普遍存在“拿來主義”的命題現象：幾乎所有試題全部可以在網上檢索到原題（數字、字母、圖形都是原樣）。這樣命題的教學導向就是“逼著”師生走進“題海”、大量“刷題”，誰做得多，誰就可能碰到原題、得到高分。雖然中考試卷較少存在“拿來主義”的命題樣態，但是，其中依然存在“喜好偏向”的命題現象。對此，命題人需要自我審視，提高警惕，以進一步擺正教學導向。

（一）警惕“喜好偏向”：不可追逐“網絡流行”和“個人興趣”

1.網絡流行試題常常成為命題的“喜好偏向”。

目前，由于自媒體（如微信公眾號）的內容在微信群或朋友圈的傳播，各地一些熱點試題很快會成為網絡流行的試題，特別是經過一些地區中考試卷的“強力推薦”，往往就會成為命題的“喜好偏向”。茲舉兩例：

1.（2018年北京市中考數學卷）在平面直角坐標系xOy中，函數y=kx（x>0）的圖像G經過點A（4，1），直線l：y=14x+b與圖像G交于點B，與y軸交于點C。

（1）求k的值。

（2）橫、縱坐標都是整數的點叫作整點。記圖像G在點A、B之間的部分與線段OA、OC、BC圍成的區域（不含邊界）為W。

①當b=-1時，直接寫出區域W內的整點個數;

②若區域W內恰好有4個整點，結合函數圖像，求b的取值范圍。

2018年之后，這類考題就在北京市各個區九年級階段（月考）練習、期中（期末）試卷中流行起來。這類試題的出現，改變了有些地區以反比例函數圖像（雙曲線）為背景的幾何綜合題命題方式，對于引導師生關注反比例函數的本質有著較好的導向作用。

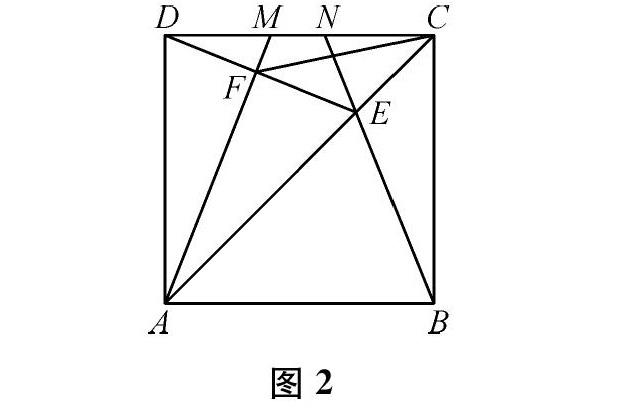
2.（2018年蘭州市中考數學卷）如圖2，M、N是正方形ABCD的邊CD上的兩個動點，滿足AM=BN，連接AC，交BN于點E，連接DE，交AM于點F，連接CF。若正方形的邊長為6，則線段CF的最小值是。

解決此題，需要利用一系列已知的或由三角形全等得到的角相等，發現點F的運動軌跡是以AD為直徑的半圓。2018年之后，很多喜歡動點軌跡的命題人就不斷圍繞這個題目進行各種改編，并拓展到了“定角定弦”問題。這類考題通常解法比較單一，且具有一定的技巧性，使得師生不斷歸納、提煉解題技巧或模型，把教學帶向對細枝末節的關注。其實，這類題的很多解題技巧價值不大：高中學習平面解析幾何知識后，很容易通過“建系，設點（或其他量），表示長度，確定最值”的路徑和方法解決。

可見，網絡流行試題本身的教學導向有好有壞。但是，一旦這樣的試題經常出現，就會被師生發現“規律”，從而“逼著”師生花費較多時間去收集、研究，進而使解題教學成為“題海”教學、“刷題”教學，至少是題型教學，造成學生基礎不實。從這個意義上看，命題者需要對網絡流行試題提高警惕：可以適當挑選好的網絡流行試題改編組卷，但是不宜過分擠占經典問題的考查空間。

2.自身教研興趣常常成為命題的“喜好偏向”。

相對于網絡流行試題，命題人自身的教研興趣更容易成為命題的“喜好偏向”——實際上，很多網絡流行試題也是因為命題人自身的教研興趣而成為命題的“喜好偏向”的。比如，命題人偏好幾何模型，往往試卷中關鍵位置的考題多是幾何綜合題;命題人喜歡繁雜運算，往往試卷中有不少復雜的運算，或者不少試題的運算結果 “不好看”。

以上文提及的考查配方法的閱讀理解題為例，其設問“強制”學生使用配方法解答，多少也是筆者的教研興趣導致的。其實，盡管配方法是一種非常重要的變形技能，但是對于因式分解問題而言，“回到定義”去思考，直接分析出另一個因式的系數特點，反而是更簡單和自然的解法。可見，基于教研興趣命制的試題，同樣可能帶來不好的教學導向，需要命題者提高警惕。

（二）擺正教學導向：重視教材“經典問題”

為了切實防范命題的“喜好偏向”（這是一件“知易行難”的事），擺正命題的教學導向，筆者以為，命題人要重視對教材的研究，挑選出教材中的“經典問題”（一般是指那些經過相當長時間檢驗保留下來的數學問題）進行改編，從而引導教學充分關注教材，促進學生學會思考，發展思維，“以不變應萬變”。限于篇幅，也舉兩例：

1.圍長方形問題。

（1）（面積最大問題）用定長l的繩子圍矩形，怎樣設定長、寬能使圍出的矩形的面積最大？

（2）（周長最小問題）當圍成的矩形的面積一定時，怎樣設定長、寬能使圍成的矩形的周長最小？

“圍長方形”問題是教材中的“經典問題”。這類問題的結論“顯而易見”，學生在小學就已熟知，但嚴謹的證明卻需要使用初中階段的數學工具。根據教學經驗，這類問題設計成考題后，難度系數都在0.5—0.6，具有很好的區分、測評功能，又有很好的教學導向。

2.正方形邊上的點（非頂點）引出的直角問題。

（1）如圖3，E為正方形ABCD的邊BC上的一個動點，連接AE，作EF⊥AE，交CD于點F。請指出圖中互余的角有幾對？

（2）在（1）的條件下，求證：∠BAE=∠CEF。

（3）如圖4，點E、F、G分別在正方形ABCD的邊AB、BC、CD上，且AE=BF=CG，連接EF、FG，求證：EF=GF。

（4）如圖5，正方形ABCD中，點E在邊BC上，連接AE，作EF⊥AE，交正方形ABCD的頂點C處的外角平分線于點F，求證：AE=EF。

正方形是接近完美的直邊圖形，其四條邊相等，四個角均為90°。以一條邊上任意一點（非頂點）為頂點在正方形內作直角，直角的邊與正方形的邊相交（相當于作出正方形的一個“形周角”，類比“圓周角”可叫“方周角””），結合正方形的邊形成的平角以及頂點處的直角，可以得到很多角互余、很多角相等以及很多（直角）三角形相似;如果加上一些線段相等的條件，可以得到很多（直角）三角形全等，進而得出更多的線段相等。上述4個小題便是基于這一“經典問題”的改編，從角互余到角相等，再到直角三角形全等（得到線段相等），最后到非直角三角形（即最大的角為135°的鈍角三角形）全等（得到線段相等），自然深入。特別值得一提的是，相比于上述蘭州市中考題，本題考查的圖形更為簡潔、基本，命制并不顯得刻意，解答無須復雜技巧，尤其是第（4）小題，即使想不到構造鈍角三角形全等，也可以發現A、E、C、F四點共圓，得到∠AFE=∠ACE=45°，或者利用正方形和外角平分線設出有關線段的長，再根據直角三角形相似（相似很容易得出，全等比較難得出）得到線段長的比例關系，通過解方程的手段解決問題（這是算的方法，比較好想，其實體現了解析幾何的思想，也體現了張景中院士改造歐氏幾何的“教育數學”思想）。

參考文獻：

[1] 劉東升.學測命題要重視“關鍵題”的教學導向——有感于一道九年級“糾錯題”[J].教育研究與評論（中學教育教學），2021（4）.

[2] 王小林.關注經典問題教學：值得重視的教研主題——從李大潛院士“懷念徐質夫老師”說起[J].中學數學月刊，2019（8）.

[3] 郭文欣.求聯求變：讓經典問題從“快思”到“慢想”[J].中學數學，2018（10）.

[4] 徐章韜.從全等、相似到面積、三角——教育數學研究之七[J].教育研究與評論（中學教育教學），2019（1）.