基于學情分析實現中學高效課堂的對策探究
林希光
摘 要:新課改下,尊重學生主體地位,以多種手段營造高效課堂,為教學工作宗旨所在,而精準的學情分析是高效課堂的有力保障,為因材施教的前提及關鍵。鑒于此,教師應認真研究課標,以本學科雙向目標為核心,進行課堂教學精心設計,擬定針對性教學方案。文章以“角的度量”為例,基于前測,予以學情把握,并基于學情,喚醒經驗、感悟本質、鞏固技能,以觸發學生“生長點”、推進“內化點”、強化“關鍵點”,經由學生真正需要的教學活動的設計,實現課堂的有效及高效性,推動教學相長。
關鍵詞:精準化;學情分析;小學數學;生本教育;高效課堂
一、 基于前測 把握學情
角的度量是學生在二年級初步認識直角、鈍角、銳角的基礎上,對角的大小概念進一步理解和拓展,屬于小學階段學生必須掌握的操作技能之一,是教學中公認的難點。
在平時的教學中,教師們通常從角的大小比較開始,希望學生在一步又一步的比較中感悟。要想準確測量出角的大小,必須要有測量標準(測量單位)和測量工具,從而引出量角器和角的單位1度。根據這樣的思路,第一次備課時,我們為了讓學生感悟度量單位的產生的必要性以及度量的本質,我們在導入部分做了如下教學設計。
導入:嘗試比較角的大小
(一)用重疊法比較活動角的大小
師:能比較出這兩個角的大小嗎?
生:∠1更大。
師:有辦法驗證一下嗎?
生:將兩個角的一條邊對齊,看另一條邊的位置。
師:用重疊法可以比價兩個角的大小。
(二)利用三角尺比較練習單上兩個角的大小
師:那練習單上這兩個角呢?還能用重疊法比較大小嗎?
生:不能,因為拿不下來。
師:那該怎么辦?試著想辦法比一比,有困難的同學可以借助三角尺比一比。
生1:用活動角做出兩個與這兩個角分別相同的角,進行比大小。
生2:用三角尺幫忙比較。我用三角尺中的這個最小的角放進去,發現∠1比兩個最小角多一些,而∠2比兩個最小角多較多,所以∠2比較大。
(三)度量單位產生的必要性
師:同學們通過操作,都比較出兩個角的大小,那∠2到底比∠1大多少呢?可以怎么辦?
生:用更小的角再量一量。
師:那如果還是量不出結果呢?
生:用更更小的角再量一量。
師:要小到什么程度呢?請同學們閱讀課本內容。
從以上的教學過程看出,教師在導入環節花費了很多時間引導學生對兩個不同大小的角進行比較,期望學生通過比較體驗度量標準不斷細化的過程,感悟度量單位產生的必要性,從而引出角的度量單位——1度。
然而,在實際教學過程中我們發現,學生對此方案存在諸多的困惑,其中最明顯的表現是,當教師讓學生對練習單上兩個角進行比較時,很多學生就已經喊出“可以用量角器量一量”,但是教師卻堅持讓學生先用三角尺上的角比一比,這一要求讓不少學生感到困惑。此外,在本課后續的教學中發現,用三角尺上的固定角來表示其他角的大小,并沒有為后面度量本質的理解起到鋪墊作用,部分學生仍然不能很快地明白幾度角實際上就是表示這個角里包含了幾個1度角。
出現這樣的問題,究其原因,是教師沒能準確把握學生的學習起點,因此,這樣的教學設計是低效甚至是無效的。那么,如何準確把握學生的認知起點?教學前測為我們提供了有力的幫助。
【前測對象】四年級一班共51名學生
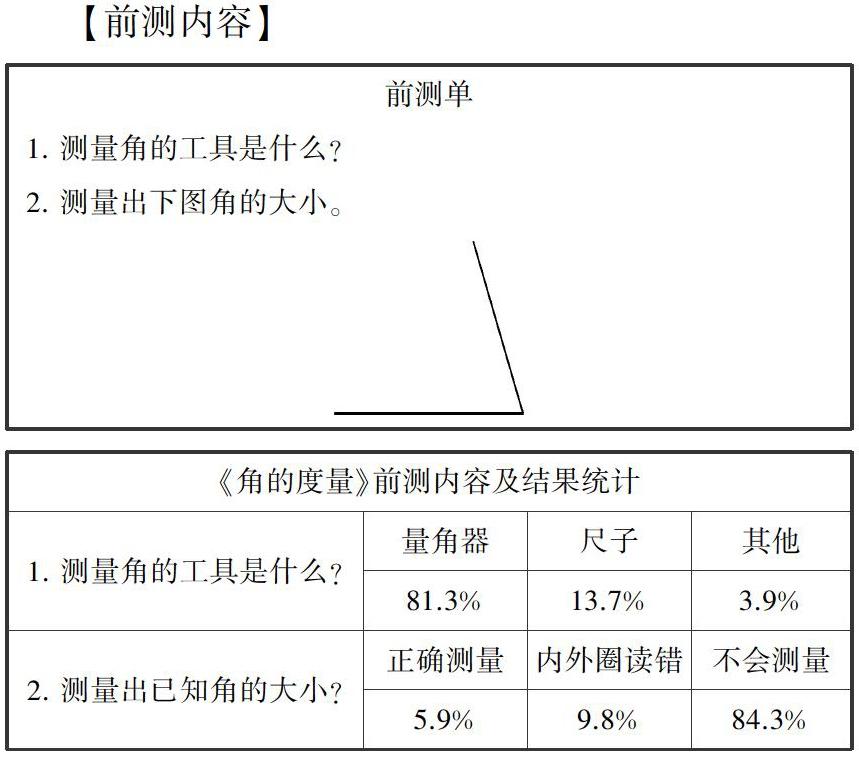
【前測內容】
隨后,我們又隨機抽取10名學生進行訪談,訪談內容為:
1. 你怎么知道量角器的?2. 你知道角的單位是什么嗎?3. 角的單位長什么樣?
訪談發現,學生們知道量角器的主要原因是購買的三角尺套裝中包含有量角器,從父母或同學的口中知道了這個半圓形的尺子是用來測量角的度數的,至于怎樣測量,并沒有得到明確答復,而個別學生測量正確的原因多是來自課外輔導班提前學習或是家長的輔導;訪談中還發現,部分學生知道角的單位是“度”,但僅是停留在聽說,并不真正了解該單位所表示的意義;繼續追問:度量角的單位應該是什么樣的?只有一位學生指出角的單位“可能是一個角”,至于為什么這么想,學生無從說起。但是經過提示:“測量線段長度的單位是一條線,測量面積的單位是一個面,那么測量角的單位會是什么樣的?”有7位學生能夠快速地反應過來,應該是個角。繼續追問:應該是個怎樣的角?大多數學生認為只能是比較小的角,并且必須要有一個統一的標準,否則每個人測量出來的結果就不一樣了。
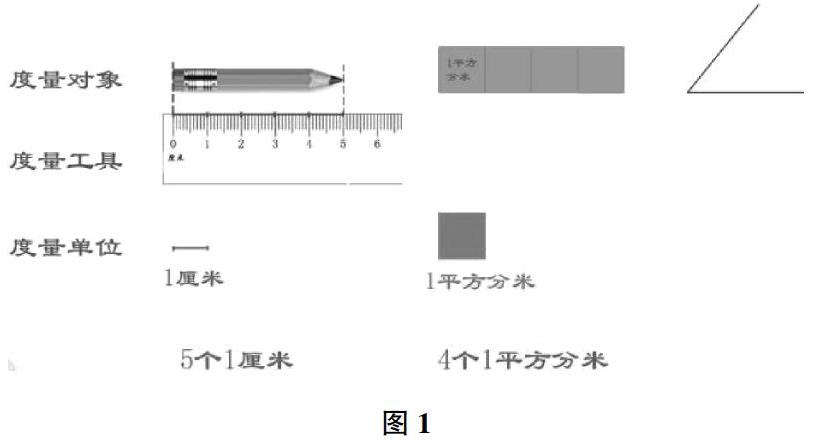
透過前測、訪談我們不難發現,絕大多數學生知道量角器是測量角度的工具,但是不知道如何準確地使用量角器。在沒有任何提示的情況下,學生對于角的單位的理解不夠深入,但是當我們把角的單位的認識放置于整個度量體系中,通過喚醒對長度單位、面積單位的認識經驗,能夠幫助學生感悟角的度量實際上就是看大角里包含有幾個小角。學生在之前的學習中,已經經歷了統一長度單位、面積單位的必要性,而角的度量單位同樣也必然要統一標準才能保證測量結果的一致性。
二、 基于學情 精準設計
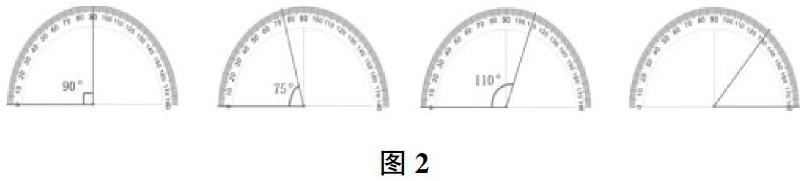
面對前測結果,引發筆者思考:1. 如何讓學生理解量角器的構造原理;2. 如何在理解度量本質的基礎上掌握量角器量角的技巧;
3. 如何幫助學生積累量角的活動經驗。基于這樣的思考,筆者將教學終點定位為“把握度量本質,積累活動經驗”,并圍繞這一目標從以下幾點展開設計。
(一)喚醒經驗,觸發“生長點”
教師組織學生參與數學活動、體驗知識的形成全過程,引領學生反思回顧學習歷程,有助于學生生成或積累相對完整的數學活動經驗。如能將學生的認知建立在已有經驗的基礎上,觸發學習生長點,將有助于學生認清知識之間的聯系,建構完善的知識體系。

