在課堂教學中融入數學文化的實踐探究

陸一烽

關鍵詞 課堂探究;數學文化;數學問題;理性思維

中圖分類號 G633.6

文獻標識碼 A

文章編號 2095-5995（2021）12-0050-03

一、在課堂教學中融入數學文化的意義

作為教材的重要組成部分，數學文化是數學教學不可或缺的重要內容。中國傳統數學文化，是一座取之不盡、用之不竭的寶藏，例如《九章算術》更相減損術、秦九韶算法、割圓術、楊輝三角、勾股定理、坐標法與吳文俊的機器證明等，都蘊含著深刻的價值觀念與文化精神追求。《普通高中數學課程標準（2017年版2020年修訂）》中指出：“數學文化是指數學的思想、精神、語言、方法、觀點，以及它們的形成和發展;還包括數學在人類生活、科學技術、社會發展中的貢獻和意義，以及與數學相關的人文活動。”新課程標準倡導數學文化應融入課程內容，并通過學業水平考試與高考命題來考查學生對于數學文化的掌握情況。

實際上，在高中數學課堂教學中往往存在數學文化內容“好看而沒有用”的現象。數學素養的核心是思維，要提升學生數學素養本質上就是發展學生的數學思維能力。因此，高中數學教學真正融入數學文化要基于課堂探究，以發展數學思維能力為前提;同時還需要讓學生在經歷用數學看待問題、分析問題、解決問題的過程中形成數學意識和積極的情感、態度、價值觀。

二、在課堂教學中融入數學文化的實踐

（一）試題呈現

2021年無錫高三數學質量檢測卷第15題是一道以中國傳統數學文化為背景的填空題。試題如下：

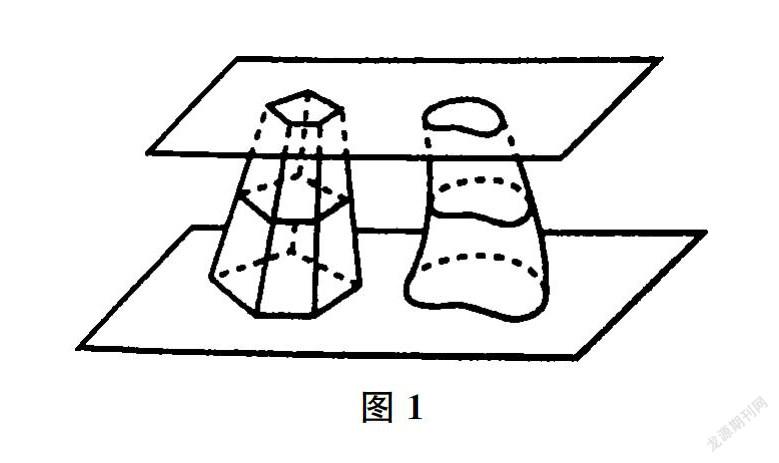
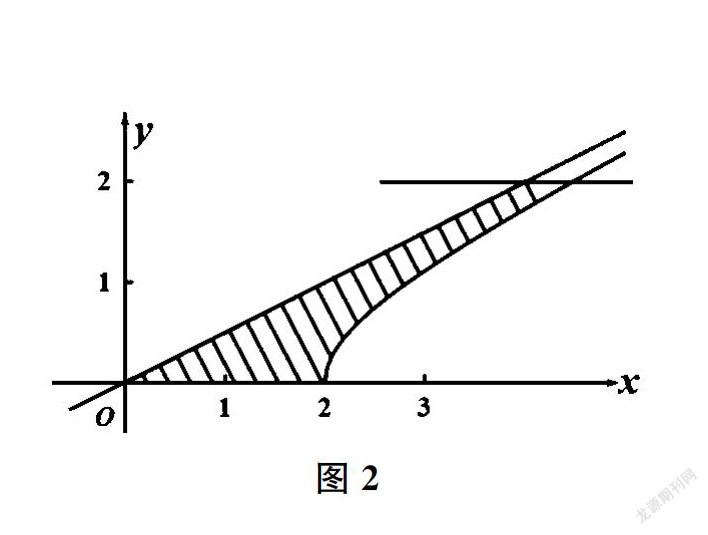
我國南北朝時期的祖暅提出“冪勢既同，則積不容異”，即祖啦原理：夾在兩個平行平面之間的兩個幾何體，被平行于這兩個平面的任意平面所截，如果截得的兩個截面的面積總是相等，那么這兩個幾何體的體積相等（如圖1）。在xOy平面上，將雙曲線的一支x²/4-y²=1（x>0）及其漸近線y=1/2x和直線V=0，y=2圍成的封閉圖形記為D，如圖2中陰影部分。記D繞y軸旋轉一周所得的幾何體為Ω，利用祖啦原理試求Ω的體積為_______。

該題文化氣息濃郁，耐人尋味，對考查學生數學運算、直觀想象、邏輯推理等核心素養有著積極的意義。但從閱卷情況來看，該題的市均分非常低，不到1分。通過對學生的調查，筆者發現學生解答該題時面臨的困難主要在于：雖然高一時了解過祖暅原理，題目中也有祖咂原理的描述，但是在解題時不知道該如何運用。

（二）追根溯源

（三）課堂探究

既然教材留下了探究的空間，而學生又往往缺少自主探究的積極性，那么教師則應該做好引路人和合作者。筆者認為，在數學教學中，教師的一個主要作用就是要引導學生學會探究。

1.提出問題

在課堂教學時，教師要先明確探究的問題。以新版蘇教版教材為例，“倒沙實驗”表面上是讓學生驗證球體積公式，其實質到底是什么？在“倒沙實驗”中，為什么要檢驗半徑為R的半球體積等于底面半徑和高都為R的圓柱，挖去一個以上底面為底面、下底面圓心為頂點的圓錐后的體積？這個想法到底是怎么出來的？怎樣用祖暅原理證明這兩個幾何體的體積相同？

2.分析問題

師：祖咂原理的適用前提是什么？

生：是兩個等高的幾何體，并且這兩個幾何體在所有等高處的水平截面的面積相等。

師：我們想象這樣一個場景，遙遠的古代，數學家正在冥思苦想球體積的計算方法，正是因為古人不知道球體積公式，所以只能探索新的計算思路。這一計算思路應該建立在充分運用祖咂原理的基礎上。

生：會不會想到構造一個與半球這個幾何體等高并且任意水平截面積相等的一個幾何體？

師：你的想象力太豐富了！大家繼續想一想這是怎樣的一個幾何體呢？

生：這個幾何體應該越往下，水平截面面積越大，越往上水平截面面積越小，直至0。

生：那這個幾何體是不是就是那個幾何體！那個底面半徑和高都為R的圓柱，再挖去一個以上底面為底面、下底面圓心為頂點的圓錐后的幾何體呢？

師：怎樣可以嚴格地證明這兩個幾何體的體積相同呢？我們來試試吧。用一個水平截面去截這兩個幾何體，假設水平截面到底面的高為h，0≤h≤R，我們先來看這個水平截面半徑為R的半球所得的截面是什么圖形？

生：應該是一個圓面。

師：它的半徑是多少呢？

師：太棒了！那么水平截面去截一個底面半徑和高都為R的圓柱再挖去一個以上底面為底面、下底面圓心為頂點的圓錐后的幾何體，所得的截面是什么呢？

生：還是圓面。

三、教學啟示與反思

為什么一道本不難的題目得分如此之低？筆者嘗試從心理學視角加以分析。從數學學習心理學角度分析，APOS的四個學習層次是合理的（如圖3所示）。

“活動”階段是學生理解概念的一個必要條件，豐富的數學文化背景是實施數學活動的良好載體。如祖咂原理中，學生通過取一摞書堆放在桌面上，輕推一下，發現這個幾何體的形狀發生改變，高度沒有發生改變，所以能直觀感受到體積也沒有發生改變。在“倒沙實驗”中，學生至少知道了半徑為R的半球體積等于底面半徑和高都為R的圓柱，挖去一個以上底面為底面、下底面圓心為頂點的圓錐后的體積。但是活動所得的經驗很多基于直觀，并不深刻。“程序”階段是學生對活動的思考，例如為什么這摞書的體積沒有改變？在教材的“倒沙實驗”中，為什么會構造這樣一個特殊的幾何體，來證明它的體積和半球的體積相等？這些都是學生對活動進行反思后，經歷思維的內化后才能抽象出來的問題。“對象”階段指通過前面的抽象認識到了概念的本質，如祖咂原理的探究中，學生終于認識到因為兩個幾何體在任意一個水平面的截面積相等，再加上它們的高相同，所以它們的體積才相同，這時祖咂原理在腦海里轉化為一個具體的對象。所有經歷的這些學習活動、程序、對象，最終和其他概念、規則、經驗等在頭腦中形成“圖式”。心理學認為，以上過程一般不能逾越。這也從心理學上解釋了為什么要重視數學探究？因為學生經過自己真正探究、理解過后的原理、概念、定理才能真正形成“圖式”且被靈活運用。

因此，教師應在課堂中真正融入數學文化，通過數學探究活動，有意識地挖掘教材中的數學文化。對于學生在自主研究時有困難的部分內容，師生可以引導學生共同探究、積極思考、厘清脈絡，這既有利于激發學生的數學學習興趣，也有利于學生進一步理解數學知識，提升學生的科學精神。對于教學重難點，尤其是重要的數學概念、定理、方法，教師要通過數學探究等活動，拓展學生數學的思維活動，豐富學生的數學活動經驗，幫助學生在生成概念、發現定理、探求證明上有所收獲。在探究過程中，教師要以數學問題為核心，以分析問題為主線，以問題的解決為目標，引導學生學會用數學的眼光觀察世界、用數學的思維思考世界、用數學的語言表達世界。

責任編輯：劉源