雙層轉角石墨烯結構的構建方法淺析

陳明星

(湖南師范大學 物理與電子科學學院，湖南 長沙 410081)

2004年，英國曼切斯特大學A. Geim教授小組從石墨中剝離出碳的單層結構——石墨烯，從此掀起了二維材料的研究熱潮[1]. 石墨烯也因此在過去的十多年中一直是凝聚態物理領域的研究熱點. 由于石墨烯的層狀結構，且層間相互作用很弱，因此人們可以通過不同的堆疊方式設計具有新奇物理性質的新結構. 比如，雙層石墨烯中兩者相對旋轉一個較小的角度時可形成莫爾條紋，該轉角結構產生的摩爾周期勢將石墨烯原胞的能帶折疊到一個很小的超胞布里淵區中，并且導致兩層石墨烯中的狄拉克電子態雜化，從而對其電子的費米速度等一系列性質產生重要影響[2-7]. 當轉角在大約1.1°時，轉角石墨烯形成的莫爾周期勢作用導致平帶的出現[8]. 該角度的雙層石墨烯被稱之為魔角石墨烯. 2018年，美國麻省工學院Pablo Jarillo-Herrero研究組在魔角石墨烯中實現莫特絕緣體和超導電性[9,10]，再次將石墨烯的研究推向高潮.

將凝聚態物理前沿科研成果引入固體物理和固體電子結構相關的課程教學，既能使學生了解前沿研究動態、培養學生的學習興趣，又能增強學生運用書本知識解決實際問題的能力. 石墨烯由于其簡單的晶體結構和特殊的能帶結構，已經被同行作為固體物理等相關課程教學的經典例子[11-14].

晶體結構決定其性質，了解晶體結構是進一步研究晶體電子結構和物理性質的前提，因此固體物理教學大綱要求學生掌握描述晶體結構的數學方法.本文結合筆者自身的教學經歷，以轉角石墨烯為例，向學生展示如何構造雙層轉角石墨烯的結構，增進學生對描述晶體結構的數學方法和晶體具有周期性這一特性的理解.

1 石墨烯的晶體結構

石墨烯具有六角蜂窩狀結構(見圖1).假設其晶格常數為a，則原胞基矢為

(1a)

(1b)

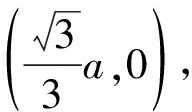
圖1 石墨烯的結構. a為晶格常數，平行四邊形代表原胞，黑色箭頭代表原胞的兩個基矢a1和a2.

2 石墨烯超胞的構建

2.1 變換矩陣

石墨烯超胞基矢Ai與原胞基矢ai的變換關系為

(2)

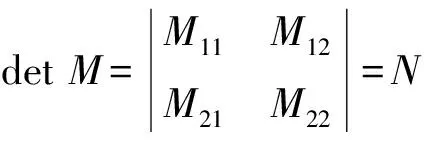
(3)

2.2 超胞結構的構造

假設原胞中第α個原子的坐標為Pα=xαa1+yαa2, 即Pα用分數坐標(xα,yα)表示，并且滿足0≤xα,yα<1，則晶體中該原子通過平移一個正格子格矢得到的原子位置坐標Pn為

Pn=(n1+xα)a1+(n2+yα)a2

(4)

ni為整數.Pn也可用超胞的基矢表示為

Pn=XαA1+YαA2

(5)

由此，可以得到

(6)

將式(3)代入式(6)可得

(n1+xα,n2+yα)M-1=(Xα,Yα)

(7)

上式給出了如何計算Pn用超胞基矢表示的分數坐標(Xα,Yα).Xα、Yα的取值可以是任意數值.若Pn位于坐標軸原點的超胞中，則0≤Xα,Yα<1.

圖2 石墨烯超胞結構.其晶格常數為黑色和淺色平行四邊形分別原胞和超胞. 黑色和淺色箭頭代表分別代表原胞和超胞的基矢. 超胞基矢用A1、A2表示.

表1 石墨烯超胞結構中各原子的坐標.

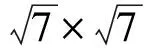
X′α=Xα-Nx

(8a)

Y′α=Yα-Ny

(8b)

Nx、Ny為可正可負的整數.上述過程還需排除重復得到的原子.上述超胞的構建也可以借助當前的晶體結構可視化軟件VESTA完成. 具體操作流程：打開VESTA操作界面并輸入相應的原胞結構，之后點擊Edit—Edit Data—Unit Cell—Transform matrix. 在Rotation matrix填入上述變換矩陣的轉置即可.

3 雙層轉角石墨烯的構建

轉角石墨烯由兩個大小相等的石墨烯超胞堆疊而成，其層間距強烈依賴于局部的原子堆垛方式，平均層間距大約在3.5 ?左右. 兩層石墨烯的相對轉角越小，超胞越大. 為保證上下兩層有轉角，其超胞變換矩陣需不同.

圖3 轉角石墨烯的構造. 黑色和淺色平行四邊形代表兩石墨烯超胞，其基矢分別用Ai和A′i表示,θ為兩超胞的相對轉角，淺色虛線沿Ri=ia1+ia2.

(9a)

(9b)

表2 部分小轉角雙層石墨烯中超胞與原胞之間的變換矩陣.

采用分數坐標的好處之一是旋轉超胞基矢時，若原子分數坐標保持不變，則晶體結構做相應的轉動.從圖3可以看出，同一原子在不同的超胞中分數坐標不同.如果使上層石墨烯超胞的基矢與下層石墨烯超胞保持一致，且原子的分數坐標(Xα,Yα)保持不變，則上層石墨烯相對下層石墨烯有θ角度的旋轉.進一步將所有原子坐標放入一個文件，并做成晶體結構可視化軟件(比如VESTA)可識別的文件格式，可得到雙層轉角石墨烯的結構圖.
圖4給出了2.13°轉角雙層石墨烯的結構俯視圖.

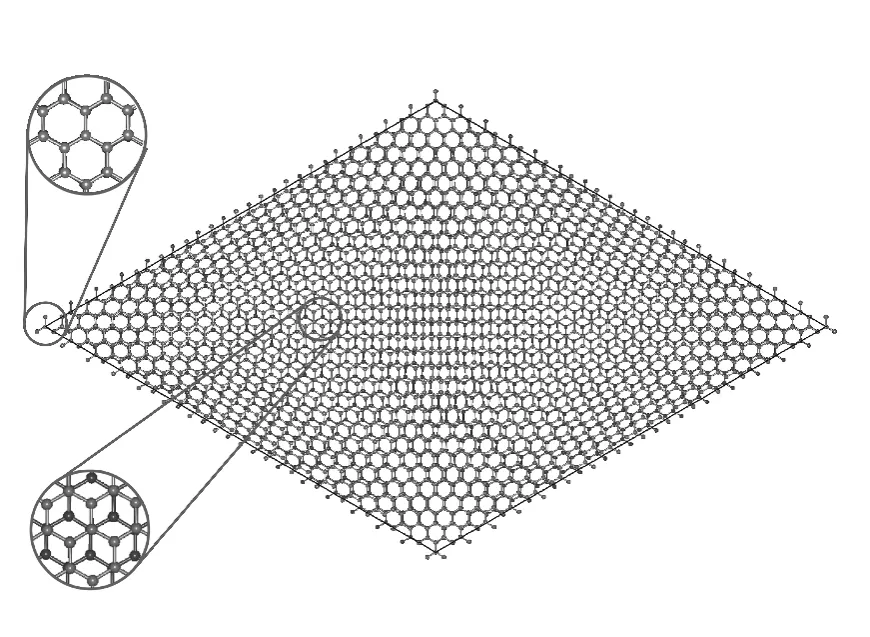
圖4 2.13°轉角雙層石墨烯的結構.兩層原子分別用不同的顏色表示并給出了AA和AB堆疊的局部原子結構，黑色平行四邊形代表一個超胞.

4 小結

本文介紹了石墨烯的晶體結構，闡述了結合晶體周期性和超胞-原胞之間的變換矩陣構造超胞結構的方法，并將其運用到雙層轉角石墨烯結構的構造，可作為固體物理課程教學的一個例子，有利于學生掌握描述晶體結構的數學方法.