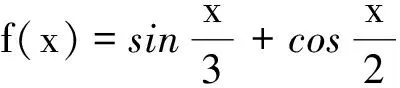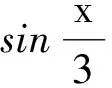一類三角函數(shù)的周期性問題探究

周思宇 (湖南省長沙市周南中學(xué) 410008)

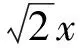
由于常值函數(shù)沒有最小正周期，故本文所研究的函數(shù)都是定義在實(shí)數(shù)集上的連續(xù)非常值函數(shù)．

1 兩周期函數(shù)之和的周期性

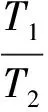
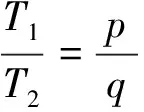
這里的T可以視為T1與T2的“公倍數(shù)”.公倍數(shù)與最小公倍數(shù)原是在自然數(shù)范圍內(nèi)考慮，這里借用這一名稱是為了方便，現(xiàn)對其意義作一個說明：若干個實(shí)數(shù)的公倍數(shù)是指同時是其中每個數(shù)的整數(shù)倍的數(shù)，最小公倍數(shù)是公倍數(shù)中最小的一個正數(shù).[2]

根據(jù)引理1我們可以知道，y=sinx+sin 2x是周期函數(shù)，2π是它的一個周期.

推論設(shè)f1(x)，f2(x)，…，fn(x)都是實(shí)數(shù)集M上的周期函數(shù)，T1，T2，…，Tn分別是它們的周期，若T1，T2，…，Tn中任意兩個之比為有理數(shù)，則這n個函數(shù)的和(或差、積、商)也是M上的周期函數(shù)，周期是T1，T2，…，Tn的一個公倍數(shù).

對于引理1與推論有三處需要說明：

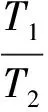
(2)引理1只是對兩個函數(shù)的和(或差、積、商)的周期性提出了一個充分條件.也就是說兩個非周期函數(shù)或者一個周期函數(shù)與一個非周期函數(shù)的和(或差、積、商)也有可能是周期函數(shù)．例如，f1(x)=sinx+x與f2(x)=sinx-x都不是周期函數(shù)，但f1(x)+f2(x)是周期函數(shù)．

(3)如果引理1中T1，T2都是最小正周期，則T=pT2=qT1不一定是f1(x)與f2(x)的和(或差、積、商)的最小正周期.例如f1(x)= sin2x與f2(x)=cos2x的最小正周期為π，但sin2x+cos2x=1，不存在最小正周期.

從上面可以看出，函數(shù)的周期性以及最小正周期是一個很復(fù)雜的問題．這里我們把研究范圍縮小到三角多項(xiàng)式函數(shù)，并給出一個判斷周期性的充要條件．

2 三角多項(xiàng)式的周期性

加強(qiáng)引理1的條件，可以得到如下幾個判斷函數(shù)周期性的充要條件.

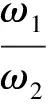
證明 (充分性)由引理易證．

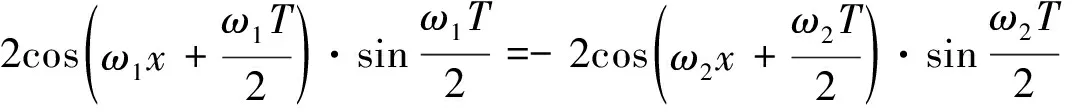
用類似方法可以得到sinω1x與cosω2x，cosω1x與cosω2x，tanω1x與tanω2x也具備類似定理1的結(jié)論.

定理1雖然給出了判斷三角多項(xiàng)式是否具有周期性的一個充要條件，但是沒有告訴我們它的最小正周期是多少.對于一般的周期函數(shù)，要具體找出最小正周期并無一般方法，但對于常見的三角多項(xiàng)式，可以找到一般方法．為了更好地得到這個方法，我們先給出一個引理.

引理2若f(x)是定義在實(shí)數(shù)集上的連續(xù)周期函數(shù)且f(x)不是常值函數(shù)，則f(x)必有最小正周期.

證明 假設(shè)f(x)沒有最小正周期，則f(x)≡f(0)，證明如下：

因?yàn)閒(x)連續(xù)，故對任意ε>0，存在δ>0，使得只要|x′|<δ，就有|f(x′)-f(0)|<ε.因?yàn)閒(x)不存在最小正周期，故可以找到f(x)的一個周期T<δ，對任意實(shí)數(shù)x，存在整數(shù)n，使得x=nT+m，0≤m

定理2[4]設(shè)f1(x)=sinω1x，f2(x)= sinω2x(ω1>0，ω2>0且ω1≠ω2)，若ω1與ω2是有理數(shù)，則f1(x)與f2(x)的和(或差、積、商)的最小正周期是f1(x)與f2(x)最小正周期的最小公倍數(shù).

證明 設(shè)F(x)=sinω1x+sinω2x，由定理1知，F(xiàn)(x)是周期函數(shù).設(shè)T是F(x)的一個正周期，要得到F(x)的最小正周期，相當(dāng)于求方程F(x+T)=F(x)的最小正值.

同理，sinω1x與cosω2x，cosω1x與 cosω2x，tanω1x與tanω2x也具備類似定理2的結(jié)論.

推論[4]設(shè)F(x)=(a1sinω1x+b1cosω1x)+(a2sinω2x+b2cosω2x)+…+(aksinωkx+bkcosωkx)，其中ωi是互不相同的正有理數(shù)，ai，bi(i=1,2,…,k)不同時為零，則F(x)的最小正周期為各項(xiàng)最小正周期的最小公倍數(shù).

由此，我們可以得出y=sinx+sin 2x的最小正周期為2π.

函數(shù)的周期性是一個非常復(fù)雜的問題，本文旨在拋磚引玉，所研究的內(nèi)容也僅僅是冰山一角.要想了解更多有關(guān)周期性的內(nèi)容，還需讀者繼續(xù)涉獵相關(guān)知識.