2021年高考試題中的數學文化

范佳清 張維忠 (浙江師范大學教師教育學院 321004)

數學承載著思想和文化，是人類文明的重要組成部分．數學文化是指數學的思想、精神、語言、方法、觀點，以及它們的形成和發展；還包括了數學在人類生活、科學技術、社會發展中作出的貢獻和意義，以及與數學相關的人文活動．《普通高中數學課程標準(2017年版2020年修訂)》強調高考試題要融入與滲透數學文化[1]．《中國高考評價體系》強調高考數學在考查過程中增加自然科學、人文與社會科學等多個領域以及現實生活、數學文化中的材料作為試題背景，考查學生運用數學知識解決實際問題的能力，促進學生數學素養的形成和發展[2]．為此，本文圍繞2021年高考中的有關數學文化的試題進行分析討論，以期為高考數學試題編擬和數學文化教學提供啟示與借鑒．

1 試題特征

2021年全國各地共有10套高考數學試卷，包括全國甲卷、全國乙卷的文科卷和理科卷，新高考卷I，新高考卷II，北京卷，上海卷，浙江卷，天津卷．其中，有關數學文化的試題共有17題(文、理科卷中相同的試題視為一道)．

借鑒張維忠等的研究，按照內容類型將高考試題中的數學文化分為數學與人文藝術、數學與科技、數學與生活以及數學史[3]，將呈現形式分為附加型、可分離型、不可分離型[4]．

從表1可以看出：從內容類型上來說，數學與生活類的試題占了大多數，涉及扶貧、視力問題、生產等公共生活方面的內容，把社會問題融入到學生的學習生活中，引導學生關注民生問題，樹立家國意識，彰顯立德樹人的教育之本．從呈現形式上來說，試題主要通過可分離型進行呈現，說明數學文化類試題仍需要注重與數學知識的關聯，避免背景素材強硬地“附加”．

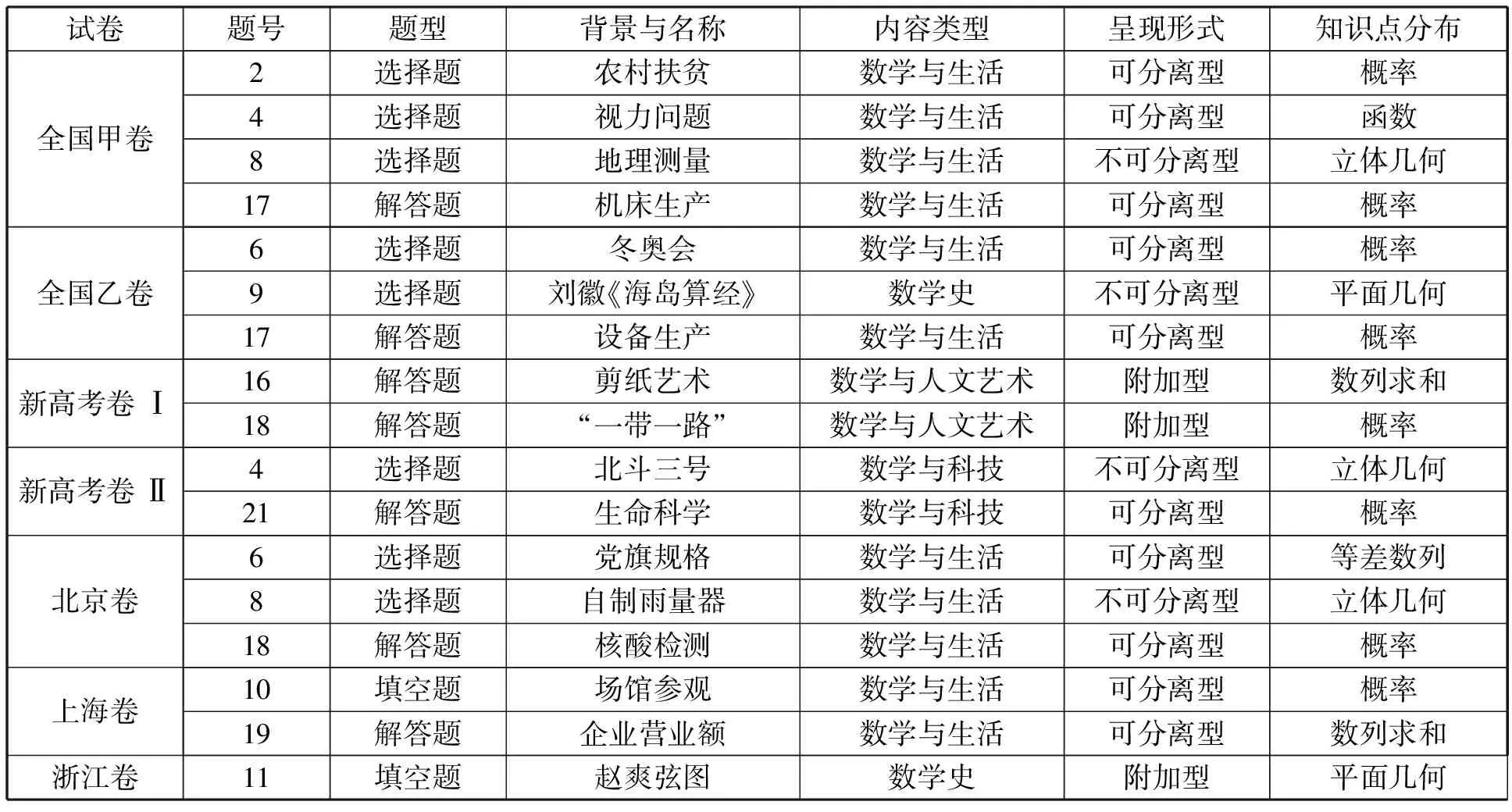
表1 2021年全國高考數學數學文化試題特征

2 試題欣賞與評析

2.1 以數學與人文藝術為背景

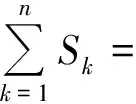
評析剪紙是中國最古老的民間藝術形式之一，能給人一種視覺上透空的感覺和藝術享受.剪紙作為一種原始藝術的載體，通過運用夸張變形的手法，將不同空間、時間的物像進行組合．此題以民間剪紙為背景，引入數列問題，為數列問題找到了真實的文化背景和現實意義，體現了數列知識與藝術的相關性及數學的應用價值．考生可以在感受中國傳統文化藝術的基礎上，抽象出其中的相關數列知識，發現對折后所得不同規格圖形的種數呈等差數列，對折后單個規格圖形的面積呈等比數列，很容易通過等差、等比數列相乘得到面積和．該題的重點在于對具體文化信息的理解和分析的能力，考查了考生的數學抽象素養．

2.2 以數學與科學技術為背景

例2(新高考卷II第21題)一種微生物群體可以經過自身繁殖不斷生存下來，設一個這種微生物為第0代，經過一次繁殖后為第1代，再經過一次繁殖后為第2代……該微生物每代繁殖的個數是相互獨立的且有相同的分布列．設X表示1個微生物個體繁殖下一代的個數．P(X=i)=pi(i=1,2,3)．

(1)已知p0=0.4，p1=0.3，p2=0.2，p3=0.1，求E(X)；

(2)設p表示該種微生物經過多代繁殖后臨近滅絕的概率，p是關于x的方程p0+p1x+p2x2+p3x3=x的一個最小正實根，求證：當E(X)≤1時，p=1，E(X)>1時，p<1；

(3)根據你的理解說明(2)問結論的實際含義．

評析如今國內外的競爭越來越體現在科技的競爭，生物科學的發展也是科學技術中不可或缺的一部分．數學教育在科技創新和人才培養上的作用也不言而喻．該題以一種微生物的繁殖作為背景，展現了數學在生物科學中的重要地位，考生通過相應的概率求解公式即可解答，難度不大.該題考查了考生的問題理解和分析的能力以及數據分析能力．

2.3 以數學與生活為背景

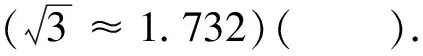
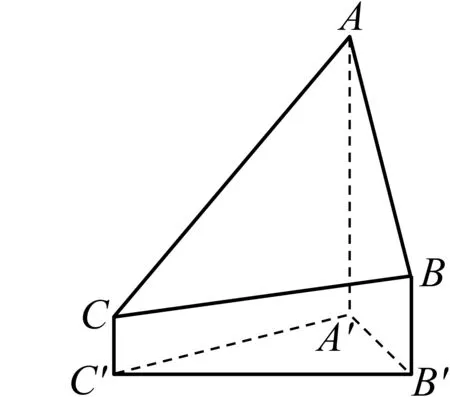
圖1

A.346 B.373 C.446 D.473

評析珠穆朗瑪峰是世界上海拔最高的山峰，珠穆朗瑪峰的高度一直是世界關注的問題．此題以珠穆朗瑪峰的高度測量為背景，介紹了三角高程測量法，引入了立體幾何問題，展現了數學與地理的緊密聯系，體現了數學的應用價值和現實意義．考生可以根據題目中給出的三角高程測量法的示意圖，借助線線關系、線面關系等立體幾何知識構建計算模型，將題目的自然語言轉換為符號語言．題目計算難度不大，重點在于考查考生的數學抽象、數學建模與空間想象能力．

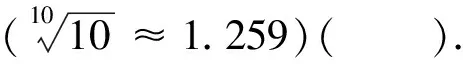
A．1.5 B．1.2 C．0.8 D．0.6

評析此題以社會廣泛關注的熱點問題作為背景，介紹了視力的五分記錄法和小數記錄法，展現了數學與社會發展的密切聯系，體現了數學的應用價值與現實意義．該題考查了函數的相關知識，考生可根據題中給出的函數解析式，通過代入L值再進行化簡后即可解答．該題考查的函數知識難度不大，但向考生傳遞了社會熱點問題，體現了數學來源于生活又服務于生活．

2.4 以數學史為背景

例5(全國乙卷第9題)魏晉時期劉徽撰寫的《海島算經》是關于測量的數學著作，其中第一題是測量海島的高．如圖2，點E,H,G在水平線AC上，DE和FG是兩個垂直于水平面而且等高的測量標桿的高度，稱為“表高”，EG稱為“表距”，GC和EH都稱為“表目距”，GC與EH的差稱為“表目距的差”，則海島的高AB=( )．

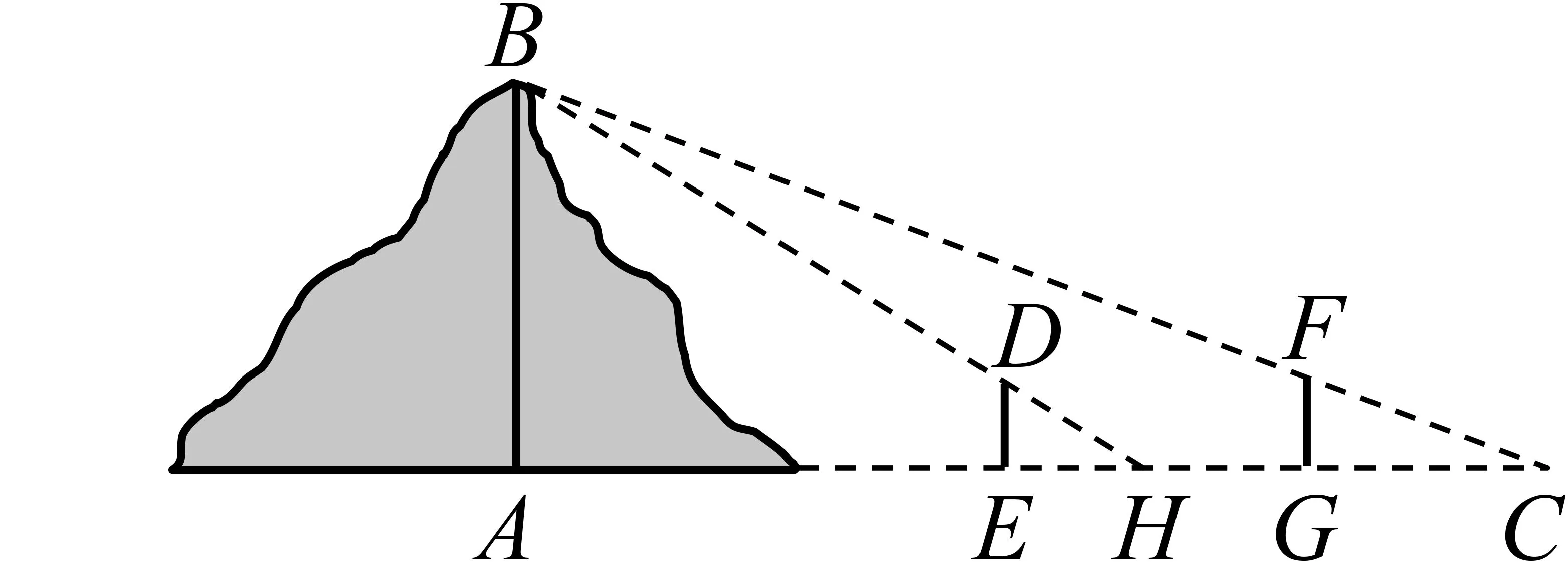
圖2

評析《海島算經》是中國學者編撰的最早的一部測量數學著作，為地圖學提供了數學基礎．該數學史背景強調了中國傳統數學文化的價值和現實意義，讓考生感受了中國古代數學測量的魅力．考生需要正確理解題干中的“表高”“表距”“表目距”等信息，結合幾何圖形解答.該題主要考查了學生對信息的理解和分析的能力、數學建模能力及數學抽象能力．

3 對命題的建議

3.1 巧妙融入人文藝術與數學史，傳遞文化價值，彰顯數學魅力

數學史具備實用性，能夠展示數學發展的歷程，也包含美學標準、智力好奇、趣味娛樂等等，可以讓師生感受到數學文化的多元性[5]；而人文藝術與數學的融合能充分展現數學的審美價值．根據統計結果可以發現，試題類型中含有人文藝術和數學史的較少；為了充分利用數學史、人文藝術的文化價值，命題者可將它們用歷史資料或者圖片的形式靈活地呈現出來，通過結合并借助數學文化中的人文精神來訓練學生的思維，提高信息的理解和分析的能力．

3.2 采用合適的呈現形式，展現數學應用價值

數學文化情境的呈現形式對于考查學生的核心素養有重要作用.2021年全國高考數學文化類試題的呈現形式主要以可分離型為主，命題者需要增加高考數學試題與實際生活、社會生產的聯系，適當地采用不可分離型的試題，讓學生通過文化理解數學或者用數學解決文化中固有的問題，展現數學文化的應用價值、科學價值、人文價值和美學價值．

3.3 設計多樣化題型，拓寬數學文化的滲透路徑

當前數學文化題型多以選擇題和填空題為主，題型較為單一．命題者可以結合學生的實際和考試的效度選擇豐富的數學文化素材，設計相應的選擇填空題和解答題；解答題的題干較長、隱含信息較多，比較注重數學思想方法的靈活運用，與題干簡潔的選擇填空題相結合，信息提取難易均衡分布，數學文化滲透自然．