學科德育視角下的數學教學與思考*
——以“古典概型”為例

吳 婷 (江蘇省無錫市第一女子中學 214002)

1 學情分析

教學對象是三星級高中高一直升班學生(初中直升高中)，基礎良好，有較強的自主探究能力、抽象概括能力和運算素養．

2 教材分析

本課時選自人教A版《普通高中教科書·數學(必修第二冊)》第十章.古典概型是概率統計領域最基本的研究對象，也是高中階段重點研究的概率模型．通過古典概型的學習，學生能進一步理解隨機事件和樣本點的關系、事件和樣本空間的關系、概率的意義，掌握研究概率模型的一般思路．

教學目標 (1)通過具體實例感受古典概型樣本點、樣本空間的特征；(2)經歷古典概型的概念形成，理解古典概型的特征及其概率計算公式，能夠計算古典概型的概率，滲透數學抽象、數學建模和數學運算等核心素養；(3)通過對歷史問題的驗證，經歷合作交流的環節，初步形成實事求是的科學態度，感受與他人合作的重要性．

教學重點 理解古典概型的特征、事件包含樣本點個數．

教學難點 判斷一個試驗是否為古典概型，將實際問題轉化為古典概型問題．

3 過程實錄

3.1 再現歷史，了解概率

文藝復興時期，意大利醫生兼數學家卡當(1501—1576)曾熱衷于骰子游戲，試圖研究不輸的方法，擲兩枚骰子，以兩枚骰子向上點數之和打賭，卡當認為押7點最有利，你認為呢？

師：在這個問題中“兩枚骰子向上點數之和為7”是隨機事件，“卡當認為押7點最有利”則表示該隨機事件發生的可能性最大．那么如何計算這個可能性的大小呢？在數學上，我們把對隨機事件發生可能性大小的度量(數值)稱為事件的概率，事件A的概率用P(A)表示．

設計意圖創設歷史素材背景下的數學情境，激發學生的研究熱情，引出概率的定義．

3.2 思考交流，建立模型

問題1讓我們穿越時空，推測卡當當時是如何得出結論“擲兩枚骰子，向上點數之和為7的概率最大”的．

生：可能他通過大量的試驗和觀察得出了結果．

師：是的，通過試驗和觀察的方法可以得到隨機事件的概率估計．但這種方法費時費力，僅能得到概率的近似值．或許他可以通過建立適當的數學模型，直接計算出這一隨機事件的概率．

問題2寫出以下試驗的樣本空間：

(1)試驗1：擲一枚質地均勻的骰子，其落地時朝上的點數；

(2)試驗2：一個班級中有18名男生、22名女生，采用簡單隨機抽樣的方式，從中隨機選擇一名學生；

(3)試驗3：拋擲一枚質地均勻的硬幣3次，其3次落地時正面朝上的情況．

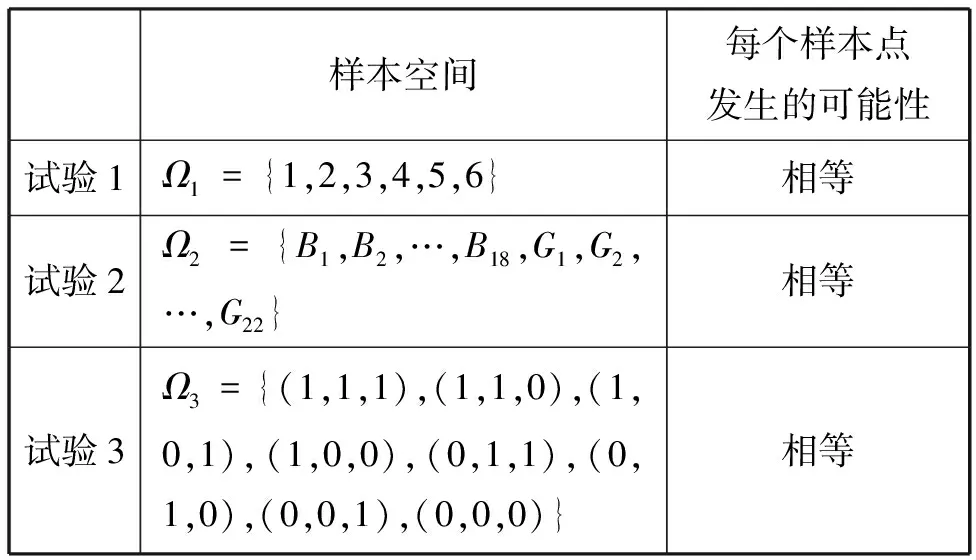
樣本空間每個樣本點發生的可能性試驗1Ω1={1,2,3,4,5,6}相等試驗2Ω2={B1,B2,…,B18,G1,G2,…,G22}相等試驗3Ω3={(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),(0,1,0),(0,0,1),(0,0,0)}相等

師：我們試著從樣本空間及樣本點的角度分析歸納三個試驗的共同特征．

生：(1)有限性：樣本空間的樣本點只有有限個；(2)等可能性：每個樣本點發生的可能性相等．

師：很好！我們將具有以上兩個特征的試驗稱為古典概型試驗，其數學模型稱為古典概型．

設計意圖通過問題設計和歸納活動，幫助學生融入歷史角色，理清古典概型的兩個基本特征，體驗概念生成和數學建模的過程．

3.3 觀察歸納，推導公式

問題3嘗試求出以下隨機事件的概率：

(1)擲一枚質地均勻的骰子，事件A=“向上點數為3”；

(2)一個班級中有18名男生，22名女生，采用簡單隨機抽樣的方式，從中隨機選擇一名學生，事件B=“抽到女生”；

(3)拋擲一枚質地均勻的硬幣3次，事件C=“恰好一次正面朝上”．

師生互動，完成表格(略).

結婚后，VCD影碟機入駐了我家，一張張光盤雖然能輕而易舉地看到時下的電影，卻沒有了電影院里的感覺。成家立業的繁雜與瑣碎，更是讓我在不知不覺的20多年中再沒有去過影院看電影了。

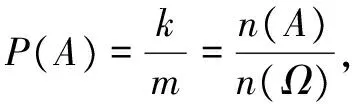
3.4 例題分析，推廣應用

例1拋擲兩枚質地均勻的骰子(分別標記為I號和II號)，觀察兩枚骰子分別可能出現的基本結果．

(1)寫出這個試驗的樣本空間，并判斷這個試驗是否為古典概型；

(2)求下列事件的概率A=“兩個點數之和是7”，B=“兩個點數相等”；C=“I號骰子的點數大于II號骰子的點數”．

學生嘗試用枚舉、樹狀圖、列表等形式探究樣本空間，得出該試驗的樣本空間中共有36個樣本點.教師投影展示學生成果：

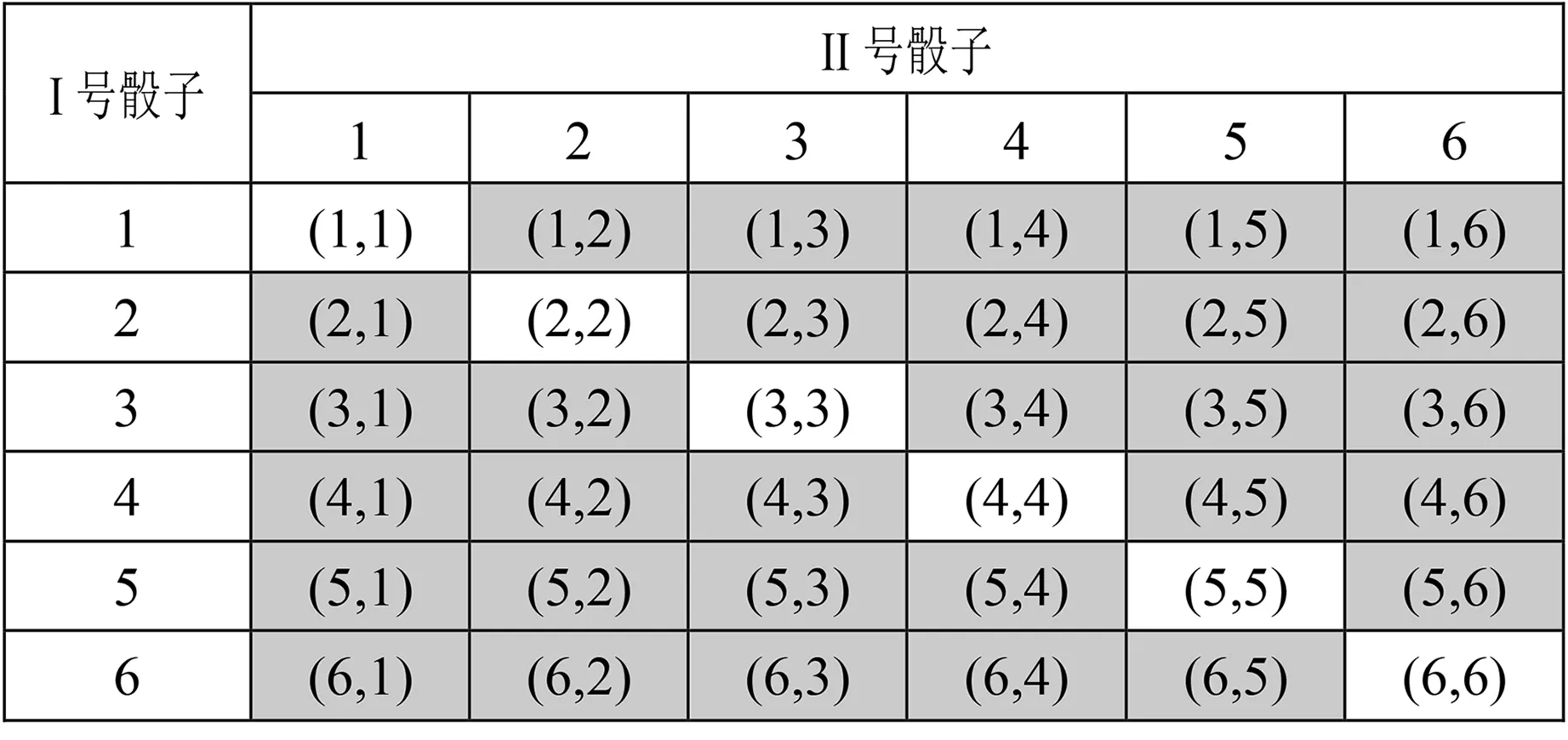
生：由于樣本空間中樣本點數量有限，骰子的質地均勻，所以各個樣本點出現的可能性相等，所以這個試驗是古典概型．

師：我們也可以用字母m表示I號骰子出現的點數，字母n表示II號骰子出現的點數，那么數對(m,n)表示這個試驗的一個樣本空間點．因此該試驗的樣本空間Ω={(m,n)|m,n∈{1,2,3,4,5,6}}．

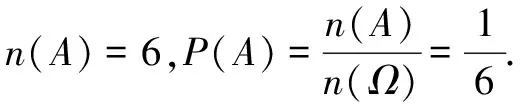
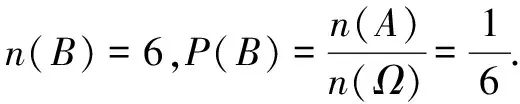
問題4你覺得卡當的推測正確嗎？為什么？(學生交流討論)

生：從表格可以看出右上角至左下角對角線上樣本點分布最多，所以卡當的推測是正確的．

師：很好，那我們能否量化這個結果呢？

生：我們小組計算了點數之和分別是2,3,…,9,12時對應的概率，從中可以看出卡當的推測正確．

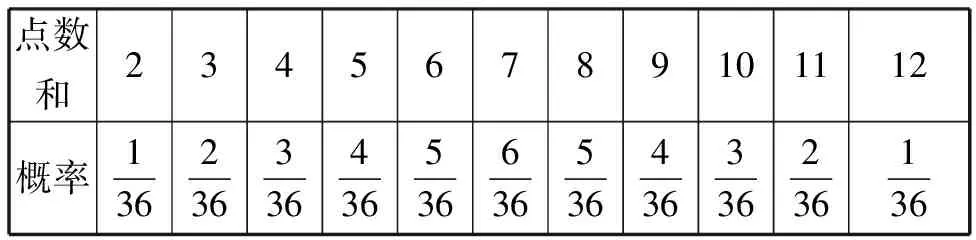
點數和23456789101112概率136236336436536636536436336236136

問題5為什么要把兩枚骰子標上記號？如果不標記會出現什么情況？你能解釋其中的原因嗎？

(師生互動，合作探討)若不給兩枚骰子標記，則無法區分樣本點(1,2)和(2,1)，如下表：

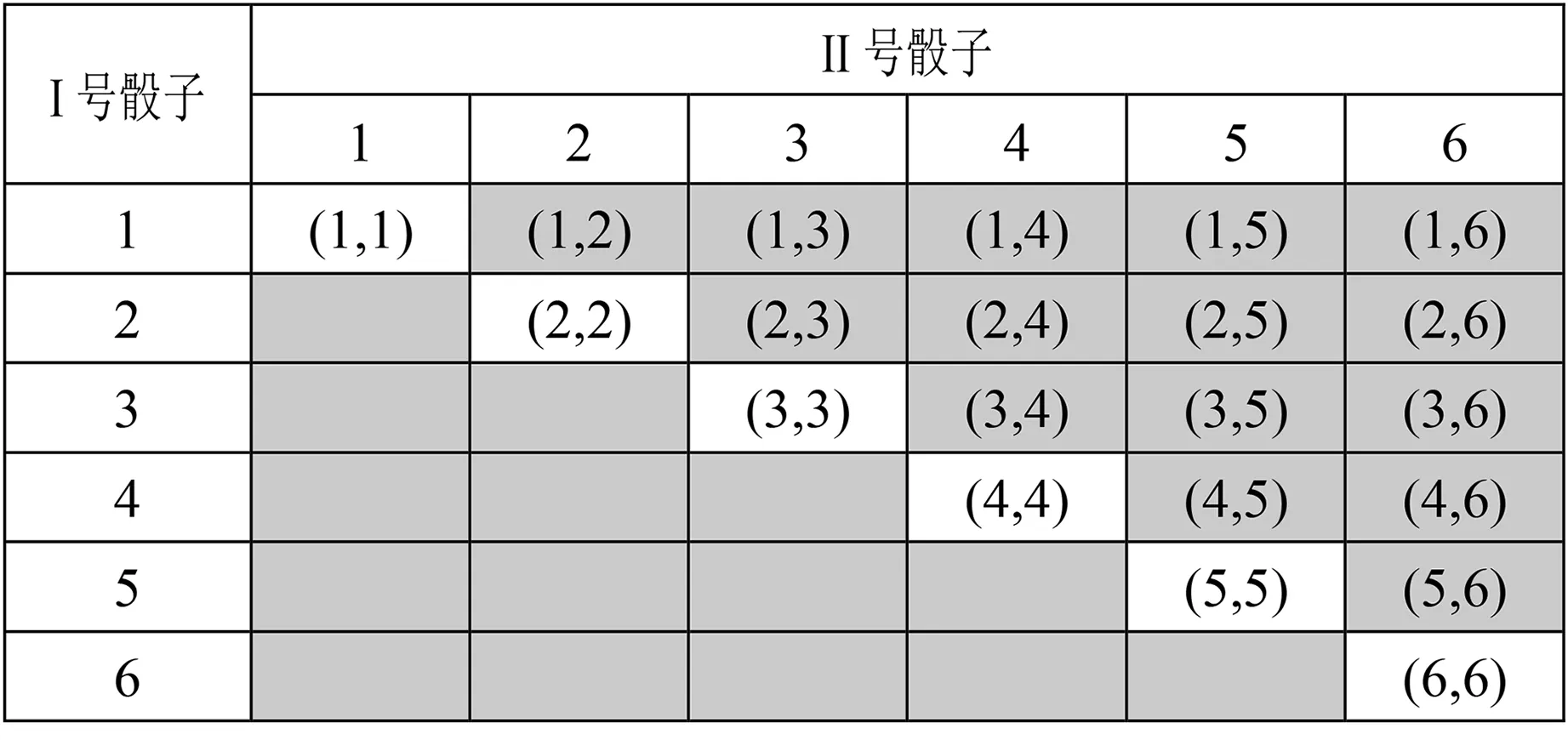
師：用古典概型計算概率時，一定要驗證所構造樣本空間中的樣本點是否滿足古典概型的第二個特征(等可能性)，否則計算出來的概率是錯誤的．

設計意圖指導學生在經歷建模運算之后，自主探究情境創設中提出的問題，引導學生通過量化對比得出問題結果，初步感知概率分布的表達，為后續學習打下伏筆．學生解決古典概型問題時，常見的錯誤是等可能性偏見，通過問題5的分析，引導學生歸納求解古典概型概率的步驟：(1)仔細讀題，收集整理題目中的各種信息；(2)判斷試驗是不是古典概型；(3)列出試驗的樣本空間和所求事件中所包含的樣本點的個數；(4)計算出古典概型的概率．

3.5 探究思考，鞏固深化

練習1 單項選擇題是標準化考試中常用的題型，一般是從A,B,C,D四個選項中選擇一個正確答案，假設某考生完全不會做，他隨機選擇一個答案，答對的概率是多少？

變式 若考試中多項選擇題(四個選項中至少有兩個選項是正確的)有四個選項A,B,C,D，隨機寫一個答案，恰好正確的概率是多少？試比較一下，在隨機選答案的情況下，是單選題容易猜對還是多項選擇題容易猜對?

練習2 齊王與田忌賽馬，田忌的上等馬優于齊王的中等馬，劣于齊王的上等馬，田忌的中等馬優于齊王的下等馬，劣于齊王的中等馬，田忌的下等馬劣于齊王的下等馬．現雙方各出上、中、下等馬各一匹分組進行一場比賽，勝兩場及以上者獲勝．若雙方均不知對方馬的出場順序，試求田忌獲勝的概率．

設計意圖通過古典概型的實際應用，在學生的思維發展區變式引申，鞏固新知．

4 教學思考

4.1 從“確定性”到“隨機性”

就數學發展的歷史進程來看，從算術到代數、從常量數學到變量數學、從確定數學到隨機數學等是數學思想方法的幾次重要突破．概率是隨機事件發生可能性大小的度量．古典概型是最簡單的概率模型，可以直接計算相關事件的概率．需要注意的是，只有在試驗結果是有限的、每個結果的出現是等可能的特征下，才能定義出古典概型中隨機事件發生的概率．因此，本節課通過拋擲兩枚骰子、連續拋擲硬幣三次等試驗，讓學生借助樹狀圖、列表格等方式，列出樣本空間，找到所有的樣本點，并找到符合題中事件的樣本點，從而進行古典概型概率的計算．

現實中還有大量隨機事件不能像古典概型一樣直接計算概率，要利用頻率來估計．因此，從單元的角度來看，本節課亦上承“確定性”，即通過確定隨機事件中樣本點數量和樣本空間Ω包含的樣本點個數來計算隨機事件發生的概率，下啟“隨機性”，即通過增加試驗的次數，得到隨機事件發生的頻率是概率的近似值．

4.2 借鑒數學史，找尋必要性

古典概型涉及的歷史素材主要是博弈問題，于是筆者結合數學史提出：卡當認為，拋擲兩枚質地均勻的骰子，押7點最有利.這一數學史問題一下就吸引住了學生，為什么數學家覺得押7點最有利？是否有科學依據？如何驗證？這一系列的問題就涌現出來了．在講解了古典概型的概念與計算公式后，再次讓學生探討這一問題，學生便能夠很清楚地講解其中的原理．

數學家史密斯認為：“數學史為數學教學改革提供重要借鑒．”數學史提供了探究的機會，并通過古今數學方法的對比，拓寬學生的思維，激發學生的興趣．[1]數學史融入數學教育是一項有趣的工作，可以從歷史上數學知識演進的關鍵進程中尋找數學家突破的方法，從而以適切的方式引入課堂教學，找尋新知引入的必要性．

4.3 古典概型是數學學科德育的重要載體

《普通高中數學課程標準(2017年版)》明確指出“數學教育承載著落實立德樹人、發展素質教育的功能”，并將“學生發展為本，立德樹人，提升素養”作為課程基本理念．古典概型是數學學科德育的重要載體，它不僅有利于培養學生的思辨能力，也是發展學生數學文化意識的優質題材．例如，2019年全國卷理科數學選擇題第6題，就是以《周易》中的卦象為背景考查古典概型的[2]．

本節課利用書本中的思考內容，結合當下新高考中的多選題這一新題型的特點，用古典概型解決了單選題和多選題哪種更難猜對的問題，再指出數學學習應當腳踏實地，夯實基礎，這里便滲透了數學學科德育，既培養了理性思維，又加強了數學學習信念．