水鹽體系汽液平衡的熱力學模型研究

劉治國，張 娜，陳 川，徐顯朕

（1.海軍航空大學青島校區，山東青島266000；2.青島大學化學化工學院）

水鹽體系一般是指水和鹽組成的體系，其熱力學性質是化工單元操作的基礎，在化學化工、海洋、地質等領域有著重要的研究價值，其相平衡性質的研究為精餾、蒸發、結晶等分離工藝提供理論依據，具有重要的研究意義。國內外許多研究者對水鹽體系汽液平衡進行了實驗和理論的研究，通過定壓法和定溫法測定了水鹽體系的蒸汽壓和沸點數據，如Robinson［1］、Patil［2］、Dinane［3］、Kolár［4］、Apelblat［5］和Chen［6］等。在研究過程中不但需要準確的實驗數據，也需要理論層面的模型發展。

近年來，許多研究者基于種種理論和模型構筑了各具特色的經驗和半經驗的模型來描述電解質溶液的相平衡性質，例如Pitzer［7-8］提出了離子相互作用模型，該模型的準確度和應用范圍較高，但是該模型的方程形式比較復雜、參數相對較多；Chen等［9-10］提出了基于NRTL的電解質溶液局部組成模型，該模型能夠成功應用于單一電解質溶液體系和部分混合電解質溶液體系相平衡的計算，但是對于復雜的電解質溶液體系的測算仍有一定困難；Lu等［11］和Maurer等［12］考慮了化學反應和物理相互作用建立了新的熱力學模型，該模型能夠計算電解質溶液體系寬溫度范圍、濃度至溶解度的活度系數。除了上述電解質溶液的活度系數模型外，在電解質溶液研究的發展過程中還出現了許多模型，如OLI MSE模型［13］、Thomsen模型［14］等，很多模型都是在以上模型的基礎上不同程度地演繹。總的來說，這些活度系數模型對于混合電解質溶液體系的計算都需要離子間的混合參數或者分子間相互作用參數，不能直接用二元體系得到的參數預測計算混合體系。

水鹽體系汽液平衡的計算在無機鹽分離過程設計中是十分重要的，特別是在蒸發結晶時的蒸氣壓和沸點等方面，對實際生產具有借鑒意義。但是對于大多數熱力學模型來說，都是在關聯計算基礎上的擴展，并不具備真正意義的預測能力，對于實際生產和工業應用具有一定的復雜性和困難性。本文針對水鹽體系的汽液平衡，在NRTL模型基礎上，基于水化作用和混合鹽假設，建立具有預測混合體系汽液平衡的活度系數模型，能夠直接應用于無機鹽工業的提純和分離計算過程。

1 NRTL擴展模型

NRTL模型于1968年由Renon等［15］提出，可以同時適用于部分互溶和完全互溶系統，針對于二元體系的過量吉布斯自由能的NRTL方程式如下：

二元體系的NRTL方程主要包含3個參數，α的值可以根據擬合情況任意規定，參考原NRTL模型，改進模型的選擇是α=0.3［15］；τi，j和τj，i是用來表示相互作用的參數。nt是溶質和溶劑的物質的量總和，mx是溶質的質量摩爾濃度。

在該模型中參考Lu and Maurer模型建立了水化作用假設，每一個溶質被h個水分子所包圍，mw是未水化的自由水濃度，表達式：

式中，hi是溶質的水化數，Ms是水的分子質量，mi是溶質的質量摩爾濃度。

在本工作中的另一個假設是把混合溶液體系中的所有溶質看成一個整體，因此混合體系可以看作是“溶質整體”和溶劑的“二元體系”，溶質-水、水和溶質的相互作用參數τw，x和τx，w的表達式如下：

τw，i和τi，w是水-溶質和溶質-水的作用參數，該參數對于每個水鹽體系都是特征化的，對于固定溫度的體系來說，這兩個相互作用參數也是固定的。但是，對于關聯計算不同溫度下的汽液平衡數據，需要有τw，i和τi，w參數與溫度的關系式。

根據式（9）可以獲得最終計算水活度的方程式。

利用式（10）可以獲得水鹽體系中水的活度數據，從而實現了NRTL擴展模型計算水鹽體系汽液平衡性質。

2 水鹽體系汽液平衡的計算

將上述NRTL擴展模型應用于水鹽體系汽液平衡的計算，首先需要根據溶液體系汽液平衡實驗數據 擬 合 模 型 方 程 中 相 應 體 系 的 參 數然后根據式（10）計算得到溶液體系中水的活度，在該模型中α的取值為0.3，h為熱力學模型的水化作用參數。

2.1 二元水鹽體系的計算

本文將擴展模型應用于21組二元水鹽體系汽液平衡的關聯計算，回歸得到了該模型在273.15～420.15 K的二元體系參數，參數結果列于表1。

對于二元水鹽體系的汽液平衡計算，將表1的參數直接代入式（10），可以直接計算該體系中水的活度性質等，二元水鹽體系的關聯結果列于表2，同時在表2中列出了擬合計算用到的原始數據來源和文獻。

表1 二元水鹽體系模型參數Table 1 Model parameters for binary electrolyte solution

表2 二元水鹽體系汽液平衡的關聯結果Table 2 Correlation of VLE data for binary electrolyte solution

2.2 混合水鹽體系的計算

對于二元以上的混合水鹽體系，例如NaCl+KCl+H2O、LiCl+CaCl2+H2O等體系，采用了關聯計算和預測計算兩種方式對混合體系的汽液平衡性質進行了計算。

筆者將采用二元水鹽體系參數直接用于混合水鹽體系汽液平衡的計算，以NaCl+KCl+H2O體系為例進行說明，通過表1分別查得NaCl+H2O和KCl+H2O體系的模型參數，將參數直接代入式（10），根據該模型的混合鹽假設，可以把混合溶液體系中的所有溶質看成一個整體，因此混合體系可以看作是“溶質整體”和溶劑的“二元體系”，因此在該模型中不存在“相互作用參數”，可以直接用二元參數進行計算。

3 結果和討論

3.1 二元水鹽體系的計算結果

本文將NRTL擴展模型應用于21組常見二元水鹽體系汽液平衡的關聯計算，回歸得到的模型參數列于表1，計算關聯結果列于表2。表2中21組二元體系的平均絕對誤差dY為0.059 kPa，平均相對誤差dP為0.88%，最大絕對誤差dY為0.097 kPa，最大相對誤差為1.82%。同時，NaCl+H2O和KCl+H2O體系的關聯計算結果列于圖1和圖2，分別為體系水活度的文獻值和計算值的結果對比，原始實驗數據分別來自于文獻［1-2］和［1-2，18-19］。從圖表的分析可以看出，NRTL擴展模型可以應用于常見二元水鹽體系水活度的關聯計算，并且計算結果較理想。

圖2 KCl+H2O體系汽液平衡關聯計算結果［1-2，18-19］Fig.2 Correlation result of VLE data for KCl+H2Osystem［1-2，18-19］

3.2 混合水鹽體系的計算結果

對于二元以上的混合水鹽體系，本文采用關聯計算和預測計算兩種方式對混合體系的汽液平衡性質進行計算。本文對14組混合水鹽體系的汽液平衡數據進行了關聯計算，結果列于表3。由表3看出，14組混合體系的平均絕對誤差dY為0.061 kPa，平均相對誤差dP為1.27%，最大絕對誤差dY為0.1 kPa，最大相對誤差為1.8%。圖3為NaCl+KCl+H2O體系中汽液平衡中溫度與蒸汽壓的文獻值和關聯計算值的結果對比，原始實驗數據來自于文獻［3，5，18-19］。從圖表結果分析可知，NRTL擴展模型可以用于混合水鹽體系汽液平衡的關聯計算，計算結果與二元體系的相當，因此進一步驗證了該擴展模型的可行性。

表3 混合水鹽體系汽液平衡的關聯結果Table 3 Correlation of VLE for mixed electrolyte solution system

圖3 NaCl+KCl+H2O體系汽液平衡的關聯結果［3，5，18-19］Fig.3 Correlation of experimental VLE data for NaCl+KCl+H2O system［3，5，18-19］

本文擴展模型不但具有良好的關聯性，同時也具有一定的預測性（見表4）。該模型可以采用二元水鹽體系參數直接用于混合水鹽體系汽液平衡的計算，二元體系參數列于表1。圖4為NaCl+KCl+H2O體系文獻值和預測計算值的結果對比，原始實驗數據來自于文獻［3，5，18-19］。通過對比圖3和圖4可以發現，關聯結果與預測結果是比較相近的，說明預測結果是比較令人滿意的。

表4 混合水鹽體系汽液平衡的預測結果Table 4 Prediction of VLE for mixed electrolyte solution systems

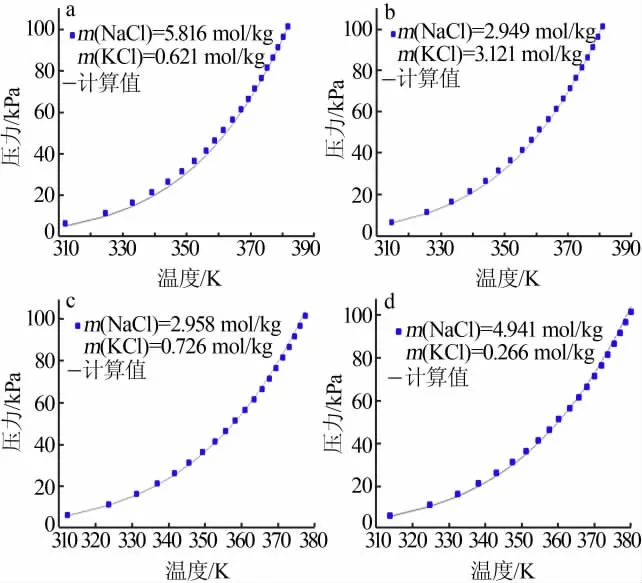
圖4 NaCl+KCl+H2O體系汽液平衡的預測結果［3，5，18-19］Fig.4 Prediction of VLE data for NaCl+KCl+H2O system［3，5，18-19］

圖5 和圖6分別為NaCl+CaCl2+H2O和LiCl+CaCl2+H2O體系文獻值和預測計算值的結果對比，原始實驗數據分別來自于文獻［16，18-19］。通過圖表分析可以看出NRTL擴展模型對于混合水鹽體系汽液平衡的預測結果是比較理想的。因此在二元體系參數獲知的情況下，NRTL擴展模型可以利用二元參數直接預測計算混合體系的汽液平衡性質。

圖5 NaCl+CaCl2+H2O體系汽液平衡的預測結果［18-19］Fig.5 Prediction of VLE data for NaCl+CaCl2+H2O system［18-19］

圖6 LiCl+CaCl2+H2O體系汽液平衡的預測結果［16］Fig.6 Prediction of VLE data for LiCl+CaCl2+H2O system［16］

4 結論

本文針對水鹽體系汽液平衡的計算，基于NRTL理論模型提出了擴展模型，該模型可以計算水鹽體系水活度、蒸汽壓、沸點等熱力學性質。通過對21組二元水鹽體系和14組混合水鹽體系的關聯計算，關聯計算結果與文獻數據具有良好的吻合性，驗證了該模型的可行性；同時，該模型可以采用二元水鹽體系參數直接用于混合水鹽體系汽液平衡的計算，不需要增加額外的混合參數，計算結果良好。因此，本文成功擴展了NRTL模型的應用范圍，可以直接用于預測計算混合水鹽體系汽液平衡的計算。