基于深度遞歸信念網絡的風電功率短期預測方法

李宏仲，付 國，孫偉卿

（1.上海電力大學電氣工程學院，上海市 200090；2.上海理工大學機械工程學院，上海市 200093）

0 引言

由于風電集中大規模接入，給電力系統安全、穩定、經濟運行帶來嚴重影響［1］，而精準的風電功率預測可以減輕其對電網的不利影響。

目前，風電功率預測方法主要分為兩大類，統計法和物理法［2］。其中，物理法是根據地表信息和氣象數據作為初始邊界條件，使用數學模型進行推理求解［3］；統計法是通過歷史數據的特性建立統計模型，進一步預測未來時刻的風電功率［4］，主要包括時間序列法和人工智能法［5］。由于各種方法都存在不同方面的誤差，為了降低單一方法的誤差上限，加權各種預測方法或者融合不同方法的優勢構建組合預測模型也是一個研究方向［6］。

相比研究不同的預測方法，從預測誤差產生的機理去提高風電預測的精度顯得尤為重要，文獻［7］從風電的波動程度、功率幅值和預測方法等因素出發，發現風電波動劇烈的時間段預測誤差明顯增大；文獻［8］采用多重分形理論提取風速波動特征并疊加預測誤差，使得預測精度進一步提高；文獻［9］研究了不同波動過程下預測誤差的分布，發現風電的不同波動類型對應不同的誤差范圍。為了分析波動誤差的影響因素，文獻［10］根據波動誤差和氣象信息之間的相關性搭建誤差修正模型；文獻［11］通過誤差分布的動態云模型對風電功率的不確定性進行精細化量測。以上文獻表明風電波動過程影響風電預測誤差，因此，本文通過圖聚類快速提取和聚合波動過程，構建分類預測模型以進一步改善風電的預測性能。

近年來，大量專家學者將深度學習應用到預測領域。文獻［12］采用遞歸神經網絡（RNN）預測風速和風電功率；但RNN在訓練過程中容易出現梯度消失的問題，使用tanh激活函數結合交叉熵損失函數可以解決梯度消失的問題。文獻［13］將深度信念網絡（DBN）和長短期記憶（LSTM）網絡用于時序預測中；文獻［14］采用DBN和堆棧自編碼（SAE）同時預測風速，結果顯示DBN的預測誤差更小。以上研究均表明采用DBN模型可以提高預測精度，但DBN弱化了時序間的相關性［15-16］。考慮到RNN能夠反映時序間的相關性，因此可用RNN取代受限波爾茲曼機（RBM）中的隱含層，并分階段堆疊RNNRBM得到深度遞歸信念網絡（DRBN）的模型結構［17］。

不同于單純引入機器學習或者人工智能的預測算法，本文應用改進搖擺窗算法識別風速波動過程，并采用廣度優先搜索鄰居（BFSN）算法對風速波動過程進行聚類。然后，根據聚類結果將風速波動劃分為低出力過程、小波動過程、大波動過程和尖峰波動過程4類。最后，通過DRBN建立相應的分類預測模型，并將待預測日的風速數據按照不同波動過程分別輸入至訓練完成的模型中進行功率預測。

1 風速波動過程的識別與聚類

隨著風速、風向、氣壓、空氣密度等氣象條件的變化，風速將出現不同程度的波動，但目前風機大多具有自動偏航系統且空氣密度在短時間內不會劇烈變化。因此，風速的不同波動是影響風電功率波動的主要原因。本文識別并聚合風速的不同波動過程作為分類預測的輸入數據。

1.1 搖擺窗算法識別風速波動過程

搖擺窗算法［9］在風速波動過程識別中僅需要人為選取一個窗寬參數ε。搖擺窗算法識別風速波動過程的原理如圖1所示，圖中以15 min為1個時段。

圖1 搖擺窗算法識別波動過程的原理圖Fig.1 Principle diagram of identifying fluctuation process by swing window algorithm

從圖1可知，ε的選取對于波動過程的識別至關重要，ε的值過小會導致識別結果中大部分為小幅波動，ε的值過大則會使得識別結果均為大幅波動而忽略了小幅的波動。在風速的波動識別中，應當根據實際情況選取合適的ε值。

搖擺窗算法的波動過程識別原理如下:

式中:Dup(t)和Ddown(t)分別為上、下搖擺窗；v0為初始時刻的風速；T為總時段；v(t)為t時刻的風速，從t=0開始計算上、下搖擺窗，尋窗過程中當滿足式（2）的約束條件時，即完成一個波動過程的識別處理。

其中，tm=mint是指取滿足Dup(t)≥Ddown(t)的最小時刻為此波動過程的終止時刻。

由式（2）可知，在波動識別過程中存在如下2種特殊情況:①很可能在一個連續同趨勢的波動過程中包含一個拐點，導致在每段波動過程中都會忽略掉一個數據點；②附錄A圖A1所示的2個連續相同趨勢的波動識別中，上、下搖擺窗未平行時便進入下一個波動過程，將會漏掉一個相同趨勢的波動過程。

因此，本文對傳統搖擺窗算法做如下改進:①每完成一次波動識別的迭代過程都要判斷終止點與前后2個采樣點的風速之差是否同號；②從上搖擺窗取得最大值時的第2個采樣點開始，分別判斷此時與前后2個采樣點下搖擺窗的數值之差是否同號。則波動過程識別的終止條件變為:

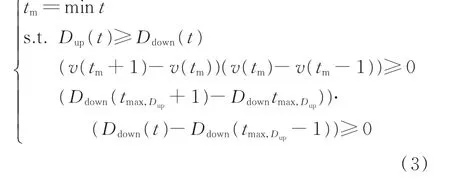
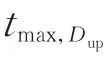
1.2 風速波動過程的聚類方法

本文基于BFSN［18］算法聚類風速的波動過程。BFSN算法在進行聚類分析時，需要輸入距離參數r和形狀參數λ，下面以風速波動過程的聚類為例說明其具體含義。

1）距離參數r

距離參數r可以理解為2個風速波動過程是否能作為鄰居的閾值，用于控制各類別之間的距離。為了減小訓練模型個數并區分不同波動對預測模型的影響，取r為相異度矩陣D［19］的平均距離，然后觀察聚類結果修正距離參數r，將波動過程聚合為低出力、小波動、尖峰大波動和大波動［8］。相異度矩陣D中 的 元 素 為 動 態 彎 曲 距 離di，j［20］，表示2個 波動過程的相似程度，若小于判別閾值r，則可視為鄰居，D的表達式如式（4）所示。

2）形狀參數λ

λ∈(0，1)用于控制聚類的形狀，若某風速類別Vt中已經包含了m個波動過程{v1，v2，…，vm}，一個新的風速波動過程vq要歸入此類，則需滿足:

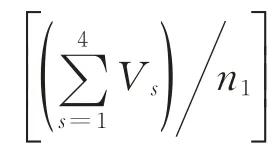
風速波動過程聚類步驟如下。

步驟1:輸入風速的波動過程集合。

步驟2:輸入聚類參數r和λ。

步驟3:求解波動過程集合的相異度矩陣。

步驟4:隨機選擇一個波動過程作為新類的初始對象。

步驟5:鄰居劃分，從新類的初始對象出發，基于BFSN算法的原則，根據距離參數r判別此波動過程的鄰居。

步驟6:搜索聚類，根據λ判斷是否將鄰居歸入此類，遍歷所有鄰居即完成了此類別的聚類。

步驟7:判斷是否完成集合中所有波動過程的聚類，若仍有未聚類的對象，轉至步驟4，直至完成集合中所有波動過程的聚類。

2 基于DRBN的風電功率預測

本文構建的DRBN的信息傳遞過程見附錄A圖A2，包括前向生成過程和誤差反饋過程。其中，誤差反饋包括2個方向:時間維度間的橫向誤差反饋和RBM相鄰各層間的縱向誤差反饋。

2.1 基于DRBN的模型架構

2.1.1前向生成網絡

DBN是Geoffrey Hinton［21］在2006年 推 導 出 來的一種生成模型，通過訓練各層的RBM可以提取并擬合數據的高階特征。但是傳統的DBN不能反映時刻之間的相關信息，考慮到RNN在時序預測方面具有較好的泛化性能，可以將RBM中隱含層信息由RNN替代共同構成RNN-RBM模型［22］，其模型結構如圖2所示。

圖2 RNN-RBM模型的結構圖Fig.2 Structure diagram of RNN-RBM model

圖2中每個藍色邊框里面表示一個RBM，綠色邊框里面包含按時間序列展開的RNN，h(t)和v(t)分別表示t時刻RBM中的隱含層的輸出和可視層的輸入，其條件生成概率P(v(t)，h(t))為:

式中:h(t)/A(t)表示在A(t)條件下的h(t)；A(t)為t時刻之前所有{(v(t?1)，h(t?1))}集合。

RNN-RBM模型帶有反饋連接的深層結構，可以表達時序數據間的相關性，因此其模型結構除了與隱含神經元和可見神經元有關外，還與上一時刻數據相關。利用式（7）和式（8）可分別計算可見層和隱含層的參數，狀態u(t)通過式（9）進行更新。

式中:b(t)和c(t)分別為t時刻可見層和隱含層的偏置；Wuv、Wuh、Wuu、Wvu為連接權 重；σ(?)為 激活函數；b(0)、c(0)、u(0)為被賦予一個隨機值的初始狀態，RNN-RBM模型參數通過使用b(0)、c(0)和權重進行訓練。

DRBN由RNN-RBM模型逐層訓練堆疊而成，見附錄A圖A3。假設DRBN有k層網絡結構，輸入序 列F={v(1)，v(2)，…，v(t)，…，v(T)}，長 度 為T；輸出的元素為O?(t)，隱含層與輸出層的權重為Q(t)，輸出層的激活函數為g(?)，則模型的前向生成過程為:

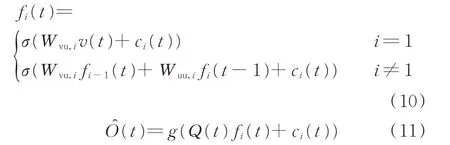
式 中:Wvu，i和Wuu，i分 別 為 權 重Wvu和Wuu的 第i個元素；ci(t)為隱含層偏置的第i個元素。

2.1.2誤差反饋網絡

誤差反饋網絡可以確保此網絡模型向全局最優的方向修正。設t時刻DRBN的輸出值為O?(t)，實際功率值為O(t)，則該時刻的預測誤差為:

通過計算式（12）的導數得到誤差E1(t)和E2(t)的梯度。

1）誤差E1(t)在各層RNN-RBM模型之間傳遞，設該方向的誤差梯度為Eg，i?1(t)，分析式（11）可知誤差梯度僅與權重Wvu，i有關，即

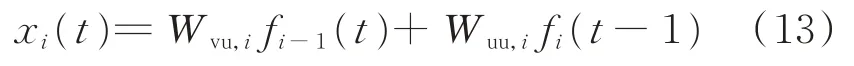
式中:xi(t)為與誤差E1(t)和E2(t)相關的中間函數；σi?1為第i?1個激活函數。

2）誤差E2(t)沿時間序列傳遞，設該方向的誤差梯度為Eg，i(t?1)，分析式（11）可知誤差梯度僅與權重Wuu，i有關，即

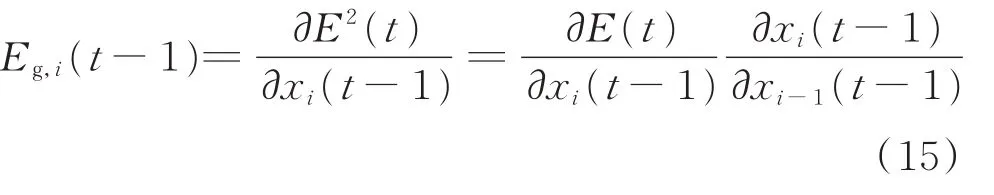
2.1.3基于交叉熵理論的損失函數

損失函數是為了統計模型輸出誤差的情況，而交叉熵可以表示2個概率分布之間的接近程度。為了比較風電歷史功率分布與模型輸出分布之間的相似程度，本節基于交叉熵理論的損失函數來有效處理均方誤差損失函數中參數更新過慢的問題，以盡量避免誤差反饋的優化過程陷入局部最優解。假設風電功率歷史數據服從分布p，模型輸出值服從分布q，則其交叉熵D(p，q)為［23］:

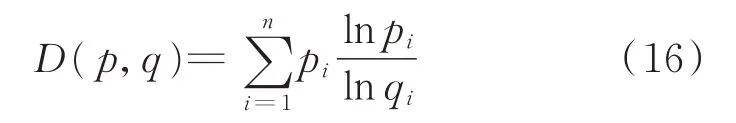
式中:pi和qi分別為分布p和分布q中的第i個元素，共有n個元素。

對式（16）變形可知，第1部分為已知的歷史功率數據，對每次損失函數的計算結果沒有影響，可以忽略不計。余下部分作為預測模型的損失函數，即

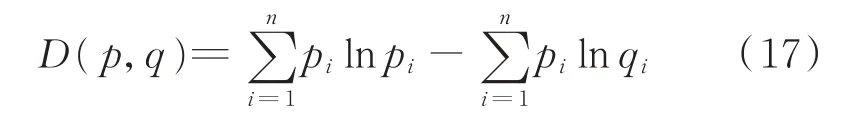
損失函數的取值越小，表示歷史功率分布與模型輸出分布之間的相似程度越高，即預測誤差越小。

2.2 基于DRBN的風電功率預測算法流程

本文首先利用第1章提出的方法識別并聚類風速波動過程，然后分類訓練基于DRBN的模型參數，最后輸入按照波動過程聚類后的風速預報數據，分類預測短期風電功率。具體算法流程見圖3。

3 算例分析

3.1 仿真數據和評價指標

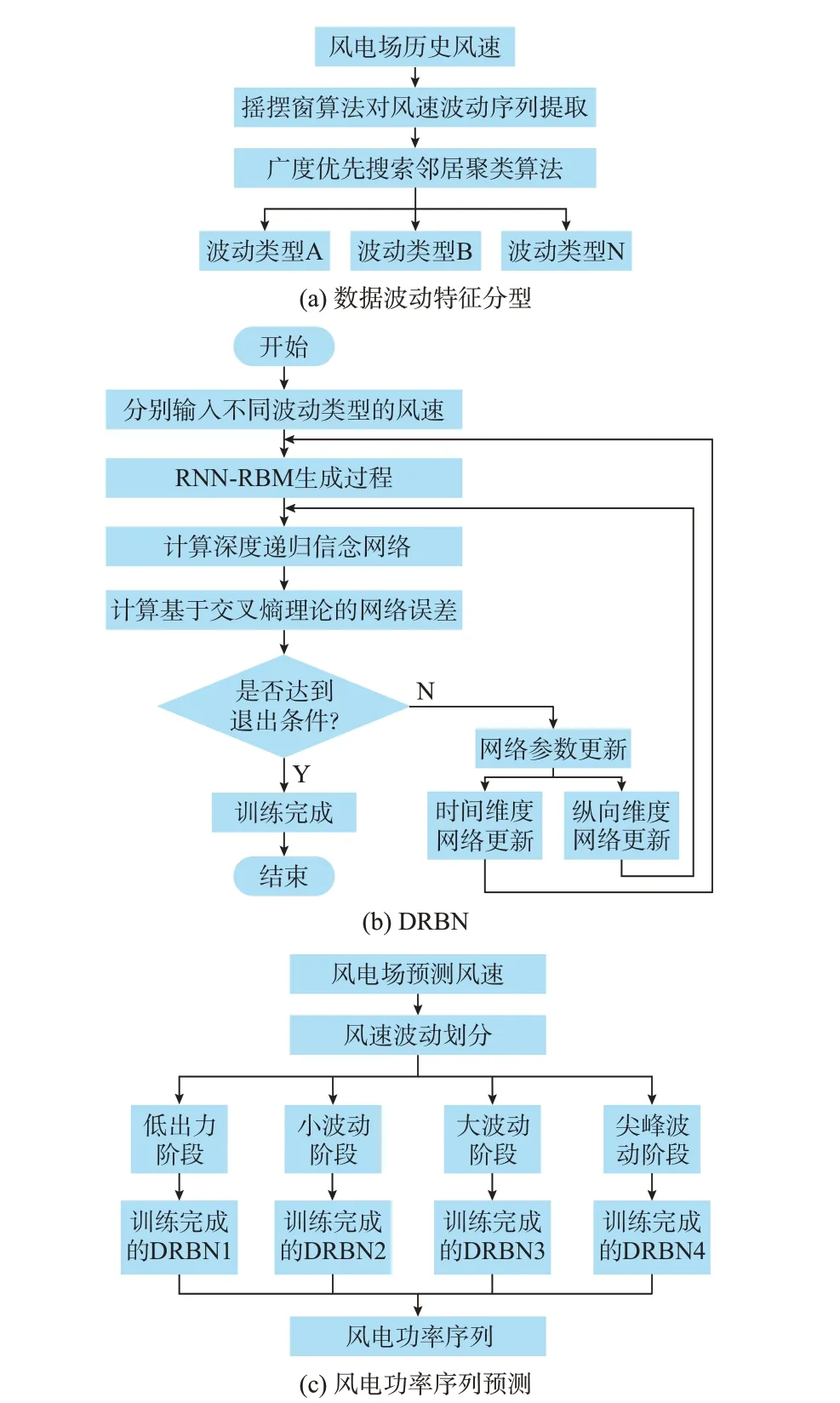
圖3 基于DRBN的風電功率預測算法流程圖Fig.3 Flow chart of wind power forecasting algorithm based on DRBN

本文選取中國某一風電場2017年11月至2018年10月的風速和對應的風電功率數據對預測模型進行驗證分析。該風電場的額定裝機容量為100 MW，將全年的風速分為大風期和小風期，以2017年11月至2018年2月的風速作為大風期訓練數據，用于預測2018年3月的風電功率。以2018年4月至2018年9月的風速作為小風期的訓練數據，用于預測2018年10月的風電功率，數據采樣間隔為15 min。

本文分別選擇傳統的DBN、支持向量機（SVM）、SAE等預測方法對預測效果進行對比分析，以驗證所提方法的有效性。預測評價指標選取平均絕對誤差（NMAE）和標準均方根誤差（NRMSE），以及評價2個數據序列相似程度的互相關系數。

3.2 風速波動數據的劃分與聚類

本文模型共計28 800個風速訓練數據，受篇幅所限選取其中144個波動過程識別后的風速數據進行展示，搖擺窗算法的窗寬ε取最大風速的5%，波動識別結果如附錄B圖B1所示。

根據1.2節風速波動聚類方法流程對模型訓練數據進行自動聚類，聚類參數r=0.2，λ=0.1，選取大風期2月和小風期7月的風速聚類結果進行展示，如附錄B圖B2和圖B3所示，共劃分了低出力過程、小波動過程、大波動過程和尖峰大波動4類波動過程，不同波動過程的樣本數量見表B1。

3.3 風速波動數據處理與網絡層數確定

搖擺窗算法提取波動過程的時間長度不一致容易致使網絡模型調優過程收斂性能差。因此，在數據輸入DRBN之前需要統一每個波動過程的數據長度。

以每個波動類型中數據個數最大的波動確定模型的結構，將小于此時間長度Tmax的波動，在其波動數據的首端和末端分別填充數據0，但是在訓練和預測過程中，考慮到波動數據時序間的相關性，設置自動忽略首端和末端為0的數據。例如某波動過程vi，樣本個數Ti＜Tmax，數據補充規則如式（18）所示，將缺少的數據平均補充至首端和末端。

通過風電功率預測結果的NMAE的變化情況確定最佳的網絡層數。

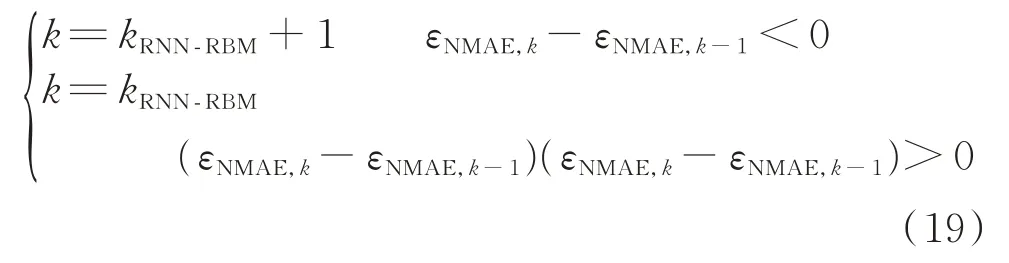
式中:k為RNN-RBM模型的網 絡層數；kRNN-RBM為初始 設 置 的RNN-RBM模 型 的 網 絡 層 數；εNMAE，k為RNN-RBM模型網絡層數為k時風電功率預測的平均絕對誤差。

由附錄B表B2可知，隨著網絡層數的增大，NMAE先減小后增大，不同的波動過程精度不再提高時具有不同的網絡層數，其中，低出力波動過程和小波動過程的最佳層數為3，大波動過程和尖峰波動過程最佳層數為4。

3.4 仿真結果分析

按照本文所提方法將低出力波動過程、小波動過程、大波動過程和尖峰波動過程的數據個數依次設置為20、20、25和15，訓練優化網絡參數，最后根據2018年3月和10月的風速預測數據，得到按照波動劃分的預測結果。

1）不同波動過程的預測結果

為了驗證本文所提方法的先進性，對比了分類和未分類預測情況下的預測精度，如表1所示。

表1 不同方法下各波動過程的風電功率預測結果誤差Table 1 Wind power forecasting errors of each fluctuation process with different methods

對于不同波動邊界點預測結果不一致的情況，以波動較平緩的預測結果為準，即按照低出力波動過程、小波動過程、大波動過程和尖峰波動過程的順序對相鄰波動邊界點的預測結果進行選取。

從表1可知:①低出力和小波動過程的預測精度高于風速快速變化的大波動和尖峰波動過程；②按照波動過程進行分類預測可降低未分類建模的預測精度；③本文所提預測方法無論相比傳統人工智能方法（如SVM）還是同自動編碼的SAE都能減小其預測誤差；④在不改變模型的情況下，提高氣象預報的預測精度，可以進一步優化預測結果，因此未來可采用數值天氣預報對不同風況下氣象數據所包含的物理特性進行更深度的分析，以期提升氣象預報信息的準確度。

利用4種方法得到的預測結果如圖4所示，可以看出，經過對DBN改進后的預測方法具有最高的預測精度，功率預測曲線和該地區實際的風機出力趨勢一致。

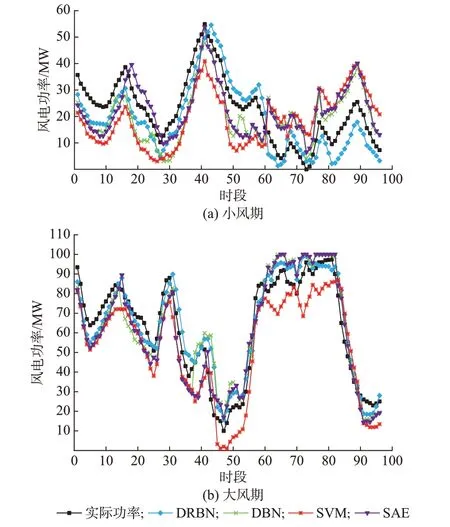
圖4 某一預測日各種預測方法對比Fig.4 Comparison of various forecasting methods for a certain forecasting day

根據預測結果，得到各種預測方法的相對誤差見附錄B圖B4。方法B、C、D、E分別代表本文所提方法、DBN、SVM和SAE方法。從相對誤差序列圖中可以看出，本文所提方法的總體相對誤差偏小，沒有極端突變誤差的出現，預測結果的穩定性較好。

2）算法效率

DRBN方法的損失函數值隨訓練次數變化趨勢對比見附錄C圖C1。由圖C1可知，未分類DRBN方法訓練60次可收斂至最優解，而通過識別訓練樣本的相似性，分類DRBN方法訓練40次即可收斂到最優解，并且除了尖峰波動其余波動類型的損失函數在收斂時均小于未分類DRBN方法。大風期和小風期下不同算法的仿真時間見表C1。

從附錄C表C1中的仿真時間可知，SAE方法耗時最長，SVM方法作為淺層模型耗時優于其他3種深度學習方法。本文方法在DBN方法的基礎上添加了反饋連接，使其訓練和預測的過程中每個時刻的預測結果增加了上一時刻的權值信息，因此，其仿真時間相比DBN模型有所增加，但預測精度高于其他3種方法。

3）橫向、縱向誤差反饋分析

為了驗證DRBN方法的橫向、縱向誤差反饋網絡對風電功率預測精度的影響，對橫向和縱向誤差反饋網絡做如下處理，一是不考慮橫向誤差反饋，二是不考慮縱向誤差反饋。以大風期為例，2種處理方式下的預測結果見附錄C表C2。

由附錄C表C2的結果可知，增加橫向、縱向誤差反饋網絡后，可以減小誤差，改善預測精度。當不考慮橫向誤差反饋時，相關性系數指標隨之降低；當不考慮縱向誤差反饋時，預測精度NMAE和NRMSE分別下降了1.09%和1.55%。

4 結語

針對目前風電功率短期預測中存在的較大誤差，本文首先識別并聚類風速波動過程，然后采用DRBN方法對不同的波動過程進行預測，最后通過和其他方法進行對比分析，得到如下結論。

1）通過對比4種預測功率的平均絕對誤差和均方根誤差，驗證了本文所提方法可以減小機器學習方法的預測誤差，提升DBN和SAE方法的預測精度，并降低了其他預測方法在波峰、波谷存在較大預測誤差的問題。

2）本文按照風速波動進行分類預測可以提高未分類的預測精度。

3）DRBN方法采用橫向、縱向誤差反饋可以有效降低單一反饋網絡下的誤差。

分析本文涉及的預測方法，SVM方法受核函數影響較大，當出力模式或者風速出現驟變時，預測結果會出現相位誤差導致預測規則無法匹配；DBN和SAE方法利用RBM與自編碼器進行預訓練，通過挖掘風速數據間隱含的非線性特征和深層變化規律，可以得到較好的預測結果，但對于風資源強烈的隨機波動預測效果不佳。因此，未來可以進一步優化尋優算法降低模型的復雜度和訓練時間，分析網絡模型的訓練參數和風況之間的相關性來提高預測精度。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。