計及電壓風險感知的交直流配電網優化調度

黃 堃，劉之涵，付 明，竇曉波，張曉燕

（1.東南大學電子科學與工程學院，江蘇省南京市 210096；2.國電南瑞科技股份有限公司，江蘇省南京市 211106；3.南瑞集團有限公司（國網電力科學研究院有限公司），江蘇省南京市 211106；4.東南大學電氣工程學院，江蘇省南京市 210096）

0 引言

直流配電網具有易于清潔能源接入、電能損耗低、電能質量高、控制方式靈活等優勢，因而被提出并受到廣泛研究［1-3］。然而，交流配電網因其自身獨有優勢仍將是配電網主要形式，直流配電網可作為補充接入交流配電網，交直流配電網必將成為一種新的發展趨勢。近年來，隨著全球環境污染和能源危機等問題不斷加劇，分布式電源得到了越來越廣泛的關注。面對大量中小容量、分散化的分布式電源接入，交直流配電網的控制運行面臨著各類電壓安全問題［4-6］。

關于交直流配電網優化調度，國內外學者已展開大量研究，文獻［7］提出了基于安全約束的交直流配電網儲能系統（ESS）與換流站協調經濟調度方法；文獻［8］提出了基于二階錐規劃的交直流配電網多時段日前經濟調度模型；文獻［9］提出了考慮多個市場參與者的交直流配電網協調能源管理方法；文獻［10］提出了考慮網絡重構的交直流配電網兩階段能量管理方法。上述方案主要以經濟性和安全性為優化目標，以配電網確定性信息為基礎展開優化，但未考慮分布式光伏（PV）、負荷等不確定性帶來的電能質量問題。

對于配電網不確定性問題，概率潮流［11-12］是評估配電網不確定性的主要研究內容之一，國內外學者將概率潮流與優化調度相結合展開了大量研究。文獻［13］考慮狀態變量的機會約束，通過粒子群算法進行確定性優化調度；文獻［14］基于魯棒約束考慮隨機變量期望值和標準差，對三相配電網進行優化；文獻［15］提出了考慮狀態變量機會約束的兩階段動態隨機優化調度模型；文獻［16］考慮電壓穩定裕度的機會約束對ESS配置進行優化。一方面，現有研究通常采用機會約束或者隨機變量期望值等手段考慮不確定性，難以直接定量感知不確定性帶來的電壓安全風險；另一方面，求解算法通常采用粒子群等智能算法，算法的收斂性和尋優性難以保證。且現有研究尚未從多時間尺度綜合考慮配電網經濟性和安全性。

針對上述問題，本文從多時間尺度考慮配電網經濟性和安全性，兼顧考慮確定性信息與不確定性信息，提出了一種計及交直流配電網電壓風險感知的優化調度方案。日前決策調度基于確定性預測信息，以經濟性為目標制定各時段運行計劃；日內風險調度考慮PV和負荷超短期不確定性的概率預測信息，建立電壓風險感知體系，以配電網電壓安全運行風險最小為目標，修改日前調度方案。根據目標函數特點，對交直流配電網潮流模型進行合理二階錐松弛，保證求解的尋優穩定性和計算效率。最后，通過算例仿真說明本文方案可以在保障交直流配電網經濟運行基礎上，消除電壓安全風險。

1 調度框架

交直流配電網系統拓撲如圖1所示，主要包括3個部分:交流配電網、直流配電網和柔性換流站，柔性換流站通常為電壓源型換流器（VSC）。

圖1 交直流配電網優化調度框架Fig.1 Optimal dispatch framework of AC/DC distribution network

交直流配電網中可控單元分為連續控制型和離散控制型2種，連續控制型包括ESS、PV和VSC，離散控制型包括電容器組（CB）。

其中，VSC參與配電網優化調度時，需要考慮其控制模式和控制特性。VSC控制可以分為Vdc-Q控制、Vdc-Vac控制、P-Q控制和Vac-P控制［17］。對于圖1所示交直流配電網，VSC一般采用主從控制模式，即主站采用Vdc-Q控制模式，從站采用P-Q控制模式。主從控制模式下，VSC一方面可以改變交直流配電網線路潮流大小和方向，另一方面可以對交流配電網進行無功功率補償。

針對上述交直流配電網調度框架，考慮日前預測存在偏差以及日內超短期存在波動性，本文提出一種計及電壓風險感知的日前日內優化調度方案，日內調度在日前基礎上進行指令修正。

考慮到離散型設備一般存在每日動作次數約束，而日內調度僅在單個時間節點進行，無法考慮全天動作次數約束，因此在日內階段離散型設備運行計劃不參與調整；同時，考慮到ESS充放電功率調整會影響配電網的全天用電成本，ESS運行計劃也不參與日內階段的調整。

2 日前決策調度模型

2.1 目標函數

日前決策調度基于預測信息的確定值，以配電網用電成本最低和系統網絡損耗最小為目標，其中，網絡損耗包括交流配電網網損、直流配電網網損和VSC內部損耗，目標函數為:

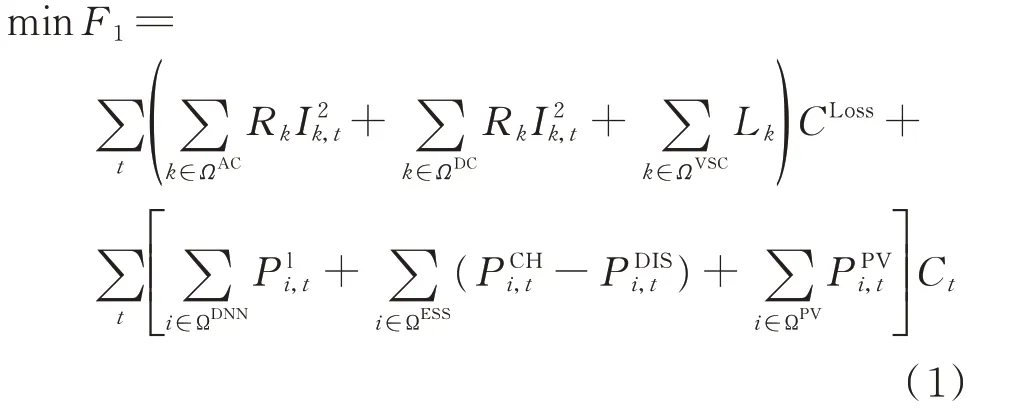
2.2 約束條件

1）CB運行約束

3）PV運行約束

交流系統中PV具有有功和無功功率調節能力，直流系統中PV具有有功功率調節能力，但本文考慮不削減PV有功出力以保證新能源發電的完全消納，僅利用交流系統中PV的無功調節能力，無功調節約束如下:

式中:ΩDNL為配電網線路集合；Vi，max和Vi，min分別為第i個節點的電壓允許最大、最小值；Vi，t為t時刻第i個節點的電壓幅值；Si，max為第i條線路的最大傳輸容量；Pi，t和Qi，t分別為t時刻第i條線路的有功、無功功率。

配電網運行時存在電壓臨近越限（near violation，NV）的情況［18］，即在電壓接近安全運行邊界但未達到邊界閾值時，有電壓越限的可能，且此時系統安全儲備較小，應避免此情況發生。因此，本文設定電壓運行邊界上、下閾值分別為0.95 p.u.和1.05 p.u.，當電壓超過1.04 p.u.或者低于0.96 p.u.時存在電壓臨近越限的安全風險，即Vi，max和Vi，min分別為1.04 p.u.和0.96 p.u.。

此外，還考慮交直流配電網潮流平衡約束，具體情況在第4章詳細介紹。

3 日內風險調度模型

日內風險調度基于電壓風險感知技術評判配電網的電壓安全風險，并以電壓安全風險最小為目標進行優化調度。

3.1 電壓風險感知技術

電壓風險感知基于PV和負荷的超短期概率預測信息，通過結合Nataf變換的隨機響應面法（SRSM）進行概率潮流計算，利用電壓安全風險效用函數計算下一斷面配電網的電壓安全風險。

3.1.1 基于SRSM的風險感知流程

SRSM是 一 種 不 確 定 分 析 方 法［13，19-20］，其 基 本思想在于利用Hermite混沌多項式擬合輸入變量與輸出響應的函數關系，其中，輸入變量和輸出響應均為隨機變量。該方法只需少量的輸入隨機變量樣本和確定性計算即可準確估計輸出響應的概率分布。

基于SRSM的風險感知流程包括以下4個步驟。

1）確定風險感知模型輸入輸出。

對于電壓安全風險感知，節點電壓安全風險R(V)為輸出響應；PV和負荷有功出力為輸入隨機變量，PV和負荷有功出力以n維隨機變量X=[x1，x2，…，xn]T表示，其中xn表示第n個PV或負荷節點的有功出力。R(V)與X的映射關系如下:

式中:G為配電網交直流潮流模型。

2）輸入標準化，將輸入隨機變量用一組標準隨機變量的函數關系表示。

將PV和負荷有功出力X標準化，通常選擇獨立標準正態分布向量ξ=[ξ1，ξ2，…，ξn]T作為標準隨機向量，建立X與ξ的映射關系，完成輸入標準化處理，具體過程在3.1.2節中進行詳細介紹。

3）輸出標準化，確定待求輸出響應的Hermite混沌多項式形式。

結合式（16）可建立ξ與R(V)的映射關系。將R(V)表達為以ξ為自變量的Hermite混沌多項式。Hermite多項式階數m越高時，混沌多項式的精度越高，但待定系數的個數也越大。大量實測表明，當m≥3時，增加階數m對提高精度的影響已不明顯，一般采用2階或3階的Hermite混沌多項式［21］，本文采用2階混沌多項式:

式中:a0、ai、aij為多項式待定系數，為常數項。

4）模型計算，選擇適當的采樣點，進行樣本點的模型計算，求解Hermite混沌多項式的待定系數，得到輸出響應的概率分布。

混沌多項式待定系數的個數N為:

在選擇采樣點時，如果采樣點組成的線性方程組系數矩陣行向量之間線性無關，計算精度將會明顯提高。因此采用基于線性無關原則的概率配點法，將線性相關的配點剔除掉，保證線性方程組系數矩陣可逆即達到滿秩，行向量之間線性無關。

最 后，確 定N個 采 樣 點（ξ1，1，ξ2，1，…，ξn，1），（ξ1，2，ξ2，2，…，ξn，2），…，（ξ1，N，ξ2，N，…，ξn，N）后，再結合X與ξ的映射關系確定各采樣點X的采樣值，基于潮流計算得到各采樣點的輸出響應R=[R(V1)，R(V2)，…，R(VN)]T，以待定系數矩陣A=[a0，…，ai，a11，…，aij]T為未知量，建立線性方程組HA=R，其中H為:

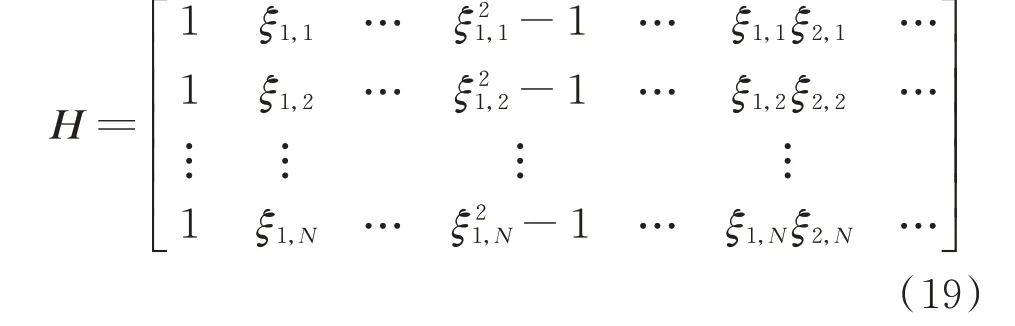
通過求解線性方程組得到待定系數矩陣A，進一步通過式（17）得到R(V)。

3.1.2 輸入變量標準化處理

SRSM可直接適用于輸入變量不具有相關性且服從標準正態分布的情況，而對于具有相關性或不服從標準正態分布的輸入變量，可通過Nataf變換［22-23］完成對輸入變量的標準化處理。

對于負荷，由于供區地域范圍較小，用電習慣具有相關性，負荷功率具有相關性，負荷有功功率在超短期上服從正態分布，負荷無功功率按照定功率因數跟隨有功功率變化。對于PV，由于供區內光照強度存在強相關性，PV出力也存在相關性，但負荷與PV之間不存在相關性［13］，PV有功出力概率密度超短期時間尺度上服從Beta分布，其概率密度函數為:

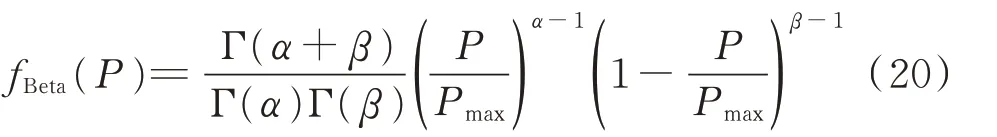
式中:fBeta為Beta分布的概率密度函數；α和β為Beta分布的形狀參數；Γ表示Gamma函數；P為PV有功出力；Pmax為PV有功出力最大值。

PV和負荷有功出力X的相關系數矩陣CX表示為:

式中:ρij為隨機變量間相關系數。

Nataf變換主要包括以下3個步驟。

1）建立輸入變量與非獨立標準正態分布向量的關系。

引入標準正態分布向量Y=[y1，y2，…，yn]T，Y中各隨機變量具有相關性，其相關系數矩陣CY可以表示為:

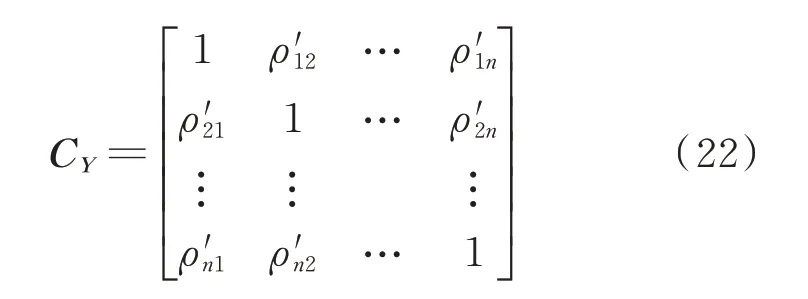
式中:ρ'ij為隨機變量間相關系數。

根據等概率原則，xi和yi的關系可以表示為:

式中:ΦY（·）為Y的累積分布函數；F（·）為X的累積分布函數。

根據Nataf變換，ρij和ρ'ij的關系如下:

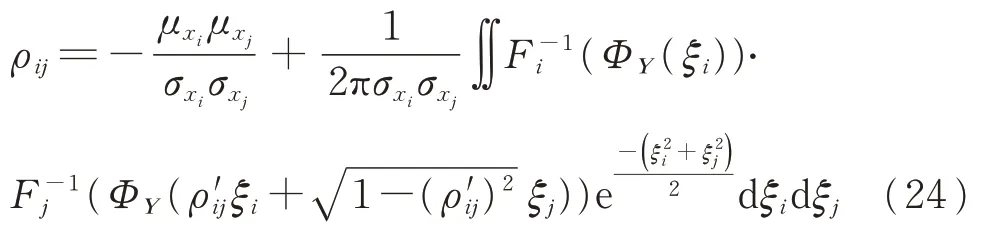
式中:μxi和μxj分別為隨機變量xi和xj的均值；σxi和σxj分別為隨機變量xi和xj的標準差；F?1j（·）為X的累積分布函數的反函數。

式（24）的詳細推導過程如附錄A所示，根據Nataf變換理論，對于服從正態分布的負荷間相關系數，式（24）可表示為ρij=ρ'ij；對于不服從正態分布的PV間相關系數，ρ'ij難以通過顯式表達式表示，為簡便計算，根據Gauss-Hermite二重積分理論，式（24）還可用下式表示:

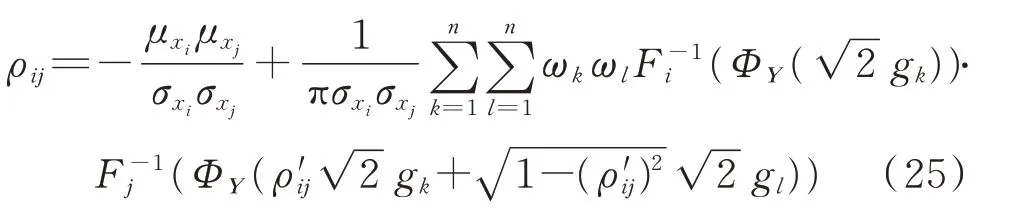
式中:gk為Gauss點；ωk為常數系數。

在Beta分布情況下，可采用二分法求取ρ'ij。

在已知CX基礎上，通過式（23）完成負荷非獨立正態分布向非獨立標準正態分布的轉換；通過式（25）求解CY中PV間相關系數部分，并結合式（23）完成PV非獨立Beta分布向非獨立標準正態分布的轉換。

2）建立非獨立標準正態分布向量與獨立標準正態分布向量的關系。

X整體轉換為非獨立標準正態分布后，X需要進一步完成向獨立標準正態分布的轉換。

將CY進行Cholesky因子分解，得到CY=BBT，其中B為下三角矩陣，則

3）建立輸入變量與獨立標準正態分布向量的關系。

最后，通過式（23）和式（26）將隨機向量X轉換為獨立標準正態分布向量，上述過程稱為Nataf變換。至此，已完成輸入變量標準化處理。在SRSM進行采樣時，基于ξ的采樣點，結合式（23）和式（26）確定負荷和PV有功出力的樣本值。

因此，結合Nataf變換的SRSM感知電壓安全風險評估流程圖如圖2所示。

圖2 電壓安全風險評估流程圖Fig.2 Flow chart of voltage safety r isk assessment

3.2 目標函數及約束

日內風險調度基于電壓風險感知技術計算結果，以SRSM計算出的配電網電壓安全風險最小為目標，目標函數為:

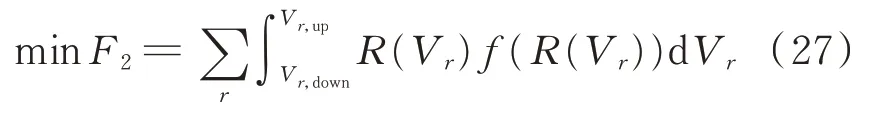
式中:r為配電網節點編號；Vr，up和Vr，down分別為第r個節點電壓Vr的最大值和最小值；f（·）為電壓安全風險的概率密度函數。

借鑒風險效用理論的效用函數，將電壓臨近越限的安全風險R(V)作為效用，將電壓偏差W作為收益，則R(V)可采用如下二次型函數對系統電壓安全風險進行評估:

式中:V為節點電壓幅值的標幺值；qi為第i個函數參數，包括q1和q2。

日內階段控制變量的約束條件與式（10）至式（13）相同，電壓和線路傳輸有功、無功期望值的約束與式（14）和式（15）相同。

4 求解算法

4.1 交直流配電網潮流Distflow模型

交流配電網Distflow潮流模型［8，24］如下:

直流配電網Distflow潮流模型如下:

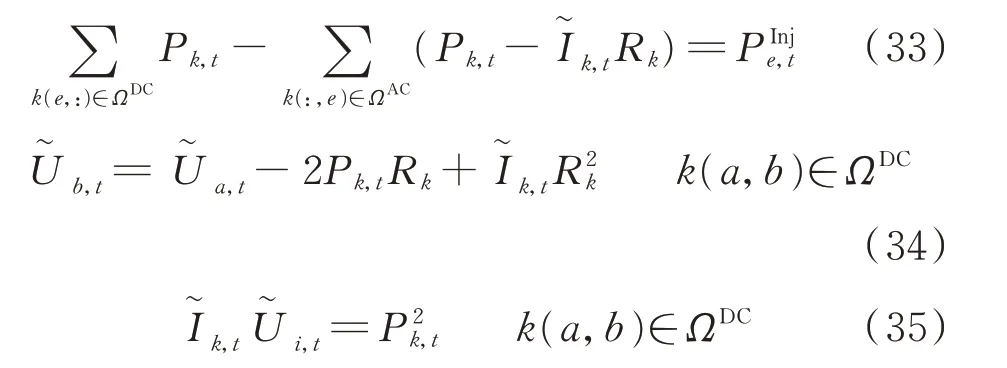
VSC潮流模型如下:

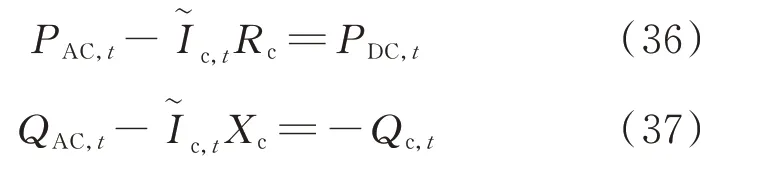
VSC理想換流器兩側電壓約束為:

式中:μ為直流電壓利用率；M為調制度。

4.2 日內目標函數的轉換

對于日內調度方案，式（27）形式的目標函數是一種積分型的非線性函數，難以參與調度方案的求解，可將其處理成方便參與求解的形式。式（27）中F2的物理含義為R(V)的期望值，F2還可用式（39）表示。

式中:ar，0為第r個節點電壓安全風險Hermite多項式中首個常數系數。日內目標函數可通過式（39）形式參與求解，式（39）的詳細推導過程見附錄A。

4.3 潮流模型的二階錐松弛

則交直流配電網潮流平衡約束如式（30）至式（38）、式（40）和式（41）所示。

對于日前調度方案，通過二階錐松弛的Distflow模型進行多時段優化調度方案進行求解。

對于日內調度方案，式（29）可以合理設置q1和q2參數消除V的一次項，使節點電壓在求解模型中僅以平方項出現。通過上述處理，式（39）的海森矩陣為半正定矩陣，日內目標函數是凸函數，式（39）的凸函數證明見附錄A。日內調度方案可通過二階錐松弛過的Distflow模型進行求解。

5 算例分析

本文算例系統采用經改造的IEEE 33節點交直流混合配電網，拓撲參數和負荷分別如附錄B表B1和表B2所示，交直流配電網額定電壓均為12.66 k V。具體拓撲如圖3所示，其相關配置見附錄A。負荷、分布式PV日前功率曲線和配電網向主網購電費用［25］分別見附錄B圖B2至圖B4。調度方案在MATLAB上進行編程，并利用YALMIP工具包和Gurobi求解器進行求解。

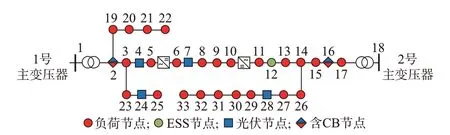
圖3 IEEE 33節點交直流混合配電網Fig.3 IEEE 33-bus hybrid AC/DC distribution network

5.1 日前決策調度結果分析

附錄B圖B5展示了日前調度前后網損的對比。由圖B5可見，每個時段網損均有降低。表1展示了日前調度前后整體結果對比。由表1可以看出，經過日前調度，配電網全天網損和用電成本均有一定下降。

表1 經濟性指標對比Table 1 Comparison of economic indicators

附錄B圖B6展示了配電網全天電壓水平。由圖B6可見，電壓均在0.96 p.u.～1.04 p.u.之間，滿足式（14）的約束，系統可正常安全運行。

附錄B圖B7至圖B9分別展示了CB、ESS和PV的優化調度結果。CB動作次數滿足規定約束。ESS功率大于0表示放電，小于0表示充電；ESS在電價較低時充電，在電價較高時放電。其中，12:00為避免電壓越上限，調度方案產生ESS充電的指令，整體達到降低配電網用電成本和削峰填谷的效果。PV無功功率大于0表示發出感性無功功率，小于0表示消耗感性無功功率。在PV發電功率較小時發出感性無功功率，為系統提供無功支撐，減小電壓降落；在PV發電較高時，吸收感性無功功率，避免電壓越上限。

附錄B圖B10展示了VSC的優化調度結果。VSC傳輸有功功率大于0時，有功功率方向為從左到右傳輸。在VSC未參與優化時，VSC主站和從站傳輸有功功率的方向均始終為交流側向直流側傳輸；在VSC參與優化后，VSC主站全天有功功率由交流側向直流側傳輸。在白天，為更好地消納左側交流電網較大的PV發電功率，VSC從站傳輸有功功率的方向為左側直流側向右側交流側傳輸，直流電網由左側交流電網供電；在晚上，PV不發電時，VSC從站傳輸有功方向則為右側交流側向左側直流側傳輸，直流電網由兩側交流電網共同供電，VSC主站和從站整體發出感性無功功率，在PV發電較高時，發出的感性無功功率減小以避免電壓越上限。VSC可通過其靈活調節傳輸有功功率和輸出無功功率的能力參與配電網優化調度。

5.2 日內風險調度結果分析

日內以12:00為例，此時PV發電功率最大，負荷較小，電壓整體水平較高。設置負荷正態分布的均值為負荷日前預測值，標準差為均值的10%，其相關系數均為0.2。設置PV的Beta分布形狀參數分別為2.5和2.06，Pmax為PV額定功率，其相關系數矩陣見附錄C式（C1），其經Nataf變換后相關系數矩陣見附錄C式（C2）。設置式（33）的q1和q2常數參數時，V≤0.96 p.u.，q1=?1/1.92；V≥1.04 p.u.，q2=1/2.08。

日內調度引入粒子群算法與本文所提求解方法進行比較，粒子群算法以式（27）為適應度。并以節點24為例，分析其電壓安全風險的概率信息。本文所提方法的求解時間為5.82 s，粒子群算法的求解時間為329.59 s。

圖4（a）展示了節點24日內調度前后的電壓概率密度函數，可以看出，日內調度之前，節點電壓概率密度在大于1.04 p.u.的區間上有非零值。經過優化后，本文所提方法的優化結果中節點電壓概率密度取值區間基本都在1.04 p.u.之下，有效降低了臨近越限的概率；粒子群算法的優化結果中節點電壓概率密度取值區間仍有一部分在1.04 p.u.之上。

圖4（b）展示了節點24日內調度前后的電壓累積分布函數圖，由圖中電壓在1.04 p.u.的取值可以看出，日內調度前臨近越限概率為62.8%，本文求解方法的優化結果中臨近越限概率為1.6%，可有效降低電壓臨近越限的安全風險，避免電壓臨近越限的情況；粒子群算法優化結果中臨近越限概率為16.6%。

此外，本文所提求解方法的誤差指標見附錄A。各支路誤差指標的散點圖如附錄B圖B11所示，可以看出，誤差指標的取值均在10?6數量級，求解精度較高。

綜上，本文所提求解方法在求解效率和精度上均優于粒子群算法，能夠滿足實際工程的應用需求。

圖5展示了系統經過日內風險調度后整體電壓均值及置信水平為95%的置信區間。由圖5可以看出，所有節點電壓平均值及其置信區間均在0.96 p.u.～1.04 p.u.之間，系統不存在電壓臨近越限的情況。

圖4 節點24電壓的概率信息Fig.4 Probability information of voltage at node 24

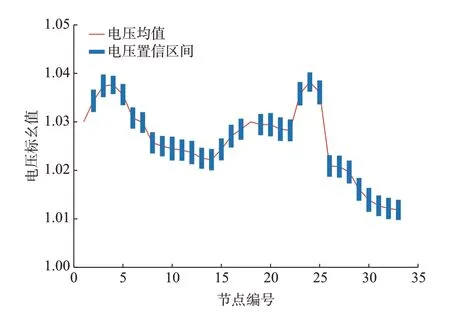
圖5 系統整體電壓及其置信區間Fig.5 Overall voltage of system and its confidence interval

表2和表3展示了日內調度與日前調度方案中PV和VSC的調整量，其中無功功率為負表示消耗感性無功功率。可以看出，各臺PV消耗的感性無功功率均增大，VSC主站由發出感性無功功率轉變為消耗感性無功功率，VSC從站降低其發出感性無功功率，PV和VSC的協調配合有效降低了電壓臨近越限風險。

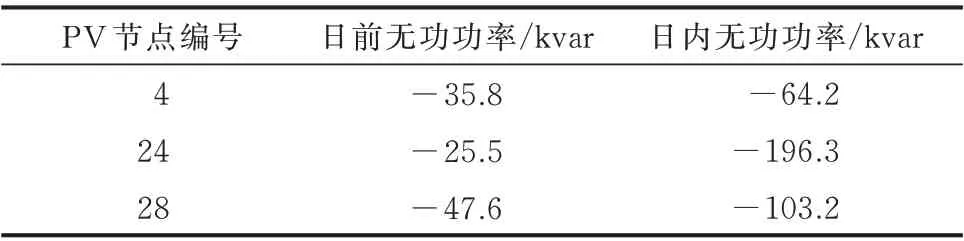
表2 日內調度方案PV調整量Table 2 PV power adjustment of intr aday dispatch scheme

表3 日內調度方案VSC調整量Table 3 VSC power adjustment of intraday dispatch scheme

5.3 整體調度結果分析

為驗證本文所提方案的有效性，本文針對不進行優化調度、只進行日前決策調度和進行日前決策-日內風險調度3類情形的系統運行狀況進行對比。其中，假設日內超短期功率預測信息中PV均服從形狀參數為2.5和2.06的Beta分布，其相關系數矩陣均滿足附錄C式（C1）；負荷正態分布的均值為負荷日前預測值，標準差為均值的10%，其相關系數均為0.2。

表4展示了3類情形的具體結果，其中，在進行網絡損耗與用電成本對比時，不進行優化調度、進行日前決策-日內風險調度與僅進行日前決策調度的負荷和PV有功功率均為日內預測期望值，負荷預測期望值與日前預測相同，PV日內預測期望值與日前稍有偏差。安全風險節點為電壓臨近越限的概率超過5%的節點。由表4可以看出，不進行優化的情形下，網損和用電成本較高，且安全風險節點較多；僅進行日前決策調度可有效降低網損和用電成本，且可減少一定數量的安全風險節點；日前決策-日內風險調度用電成本與僅進行日前決策調度相同，網損比僅進行日前決策調度略高，同時，可將安全風險節點數目降低為0，保證了系統的安全運行。

表4 系統不同情形運行狀況對比Table 4 Comparison of system operation states in differ ent conditions

6 結語

針對配電網多時間尺度上的經濟性和安全性問題，本文提出了一種計及電壓安全風險感知的交直流配電網優化調度方案，并得到以下結論。

1）日前-日內兩階段調度方案考慮離散型和連續型調節設備響應特性，從多時間尺度保證了配電網運行經濟性和安全性，且VSC作為參與優化調度時，可調節線路輸送功率大小和流向。

2）在日內階段提出一種電壓安全風險評估技術，可通過少量的輸入隨機變量樣本及確定性的計算定量評估配電網電壓運行態勢，并將評估結果作為目標函數參與日內優化調度。

3）在設計日內調度方案時，根據目標函數特點，對其參數和求解形式進行合理設置，使得本文求解方案具有良好的尋優穩定性和計算效率。

本文所提方案對負荷和PV的不確定性均采用參數分布概率模型，不適用于不確定性為非參數概率模型的情況，且暫未考慮需求側柔性負荷等有功可控元素，在未來的研究中需要進一步進行探索，以提出更加有效的調度方案。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。