測量數據野值的局部化處理模型與算法

代美泉

(西安職業技術學院機電工程學院，西安 710077)

0 引言

工程實踐中，液壓試驗臺多用于液壓泵、液壓閥、液壓馬達等的功能與性能測試，主要采集油壓、轉速、流量、振動等數據[1-2]。受多重因素影響，測量數據中往往含有大量的偏離被測信號目標真值的成分，這類成分的數據點被定義為野值，一般分為孤立型與斑點型兩種類型[3-4]。相比連續型野值成片出現的情況，孤立型野值是更為普遍的一類野值，其剔除方法主要有門限法、均方值法、肖維勒法等[5-6]。近年來，朱新巖等基于殘差特性分析，研究了野值檢測與剔除方法[7]；金學軍基于最小二乘擬合方法，對數據野值進行了剔除[8]；史椸等研究了基于方差聚類的時序數據野值識別算法[9]；葉艷等基于奇異值分解和小波分析對數據野值進行了綜合處理[10]；李釘云等以卡爾曼濾波的殘差絕對值作為判別標準，對野值點進行判別和剔除[11]。由于測量數據種類較多，不同領域測量數據的野值特性有很大不同，以上方法在具體應用上均有一定的局限性。

本文在分析液壓試驗臺測量數據野值特性的基礎上，提出了一種新型的局部化模型以滿足野值快速處理的需要，研究了一階差分野值識別算法與改進的均方誤差野值識別算法，對理論研究與工程實踐具有一定的參考價值。

1 測量數據野值特性分析

受工況調整、油泵轉動、馬達振動等因素影響，液壓試驗臺測量數據中常常混入大量的野值數據。根據不同統計特性進行分類，測量數據可分為時不變的平穩信號與時變的非平穩信號[12]。試驗臺油壓、轉速、流量等測量數據，其統計量不隨時間而變化，一般可視為平穩信號；試驗臺振動數據則表現出明顯的非平穩特性。

油泵轉速時序數據如圖1所示，可以看到：目標值為時不變的平穩信號，野值點具有孤立性。

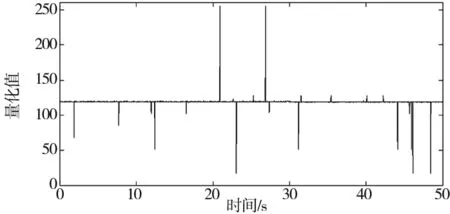
圖1 轉速數據時序圖

馬達振動時序數據如圖2所示，可以看到：目標值為時變的非平穩信號，野值點同樣具有孤立性。

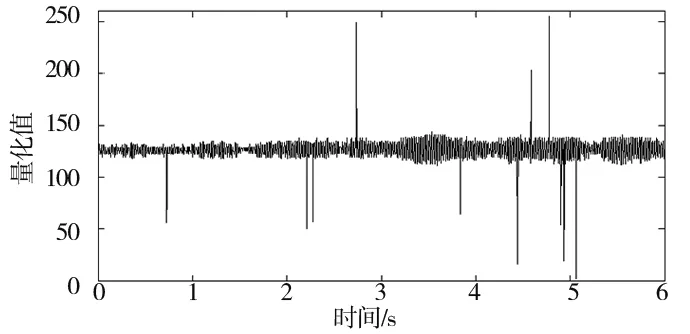
圖2 振動數據時序圖

2 測量數據野值的局部化處理模型

在分析液壓試驗臺數據野值特性的基礎上，論文提出局部化處理模型:

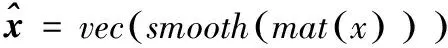
(1)

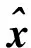
局部化處理模型主要思想為：將測量數據以n點為一個數據幀劃分為連續的m個局部幀，然后對每個局部幀進行野值判別與修補。主要算法包括信號局部化、基于一階差分的野值識別算法、改進的均方誤差野值識別算法和野值修補算法。

(1)信號局部化

定義向量矩陣化算子mat，對信號向量x進行矩陣化運算，可得到局部信號矩陣X[13]。X的每列由局部信號xi構成，xi長度為n，i=1,2…,m，32≤n≤256。

(2)

(2)基于一階差分的野值識別算法

第1步：計算局部信號xi的一階差分[14]

定義向量一階差分求解算子var，可得到局部信號xi的一階差分：

(3)

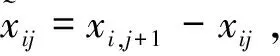
第2步：野值判別

如果

(4)

則判斷xij為野值。

(3)改進的均方誤差野值識別算法

第1步:局部信號xi的線性變換

定義向量均值求解算子mean與方差求解算子std[15]，可得到局部信號xi的均值和方差：

均值：

μ=mean(xi)

(5)

方差：

σ=std(xi)

(6)

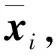
(7)

第2步:野值判別

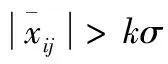
(8)

則判斷xij為野值。

其中，k的取值與局部向量xi的長度n有關，經驗取值：

k=2.50+n/160

(9)

(4)野值修補算法

如果xij判別為野值，采用該野值點前后各兩個數值的加權值來替代該野值點數據。

xij=0.2xi,j-2+0.3xi,j-1+0.3xi,j+1+0.2xi,j+2

(10)

3 基于一階差分的數據野值處理

應用一階差分算法，對圖1所示的平穩數據野值點進行自動識別與修補，數據長度2048點，迭代2次的識別結果如圖3所示，修補結果如圖4所示，可以看到：論文算法對這部分野值可以進行有效地識別處理。

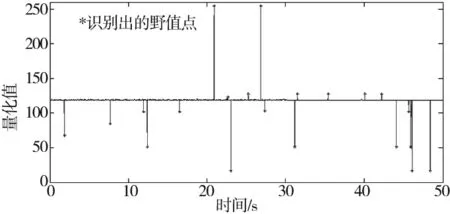
圖3 轉速數據野值識別結果圖

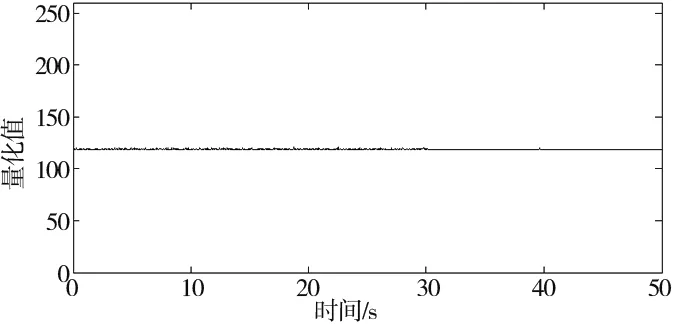
圖4 轉速數據野值修補結果圖

4 基于改進均方誤差算法的數據野值處理

用論文改進的均方誤差算法，對圖2的非平穩數據野值進行自動判別與修補，數據長度2048點，迭代2次的識別結果如圖5所示，修補結果如圖6所示。可以看到：所有野值均被正確識別并得到了恰當修補。

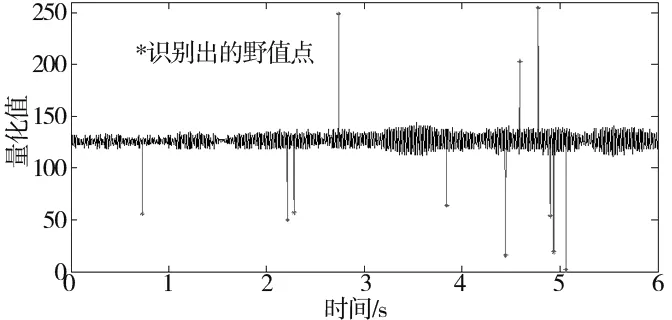
圖5 馬達振動數據野值識別結果圖

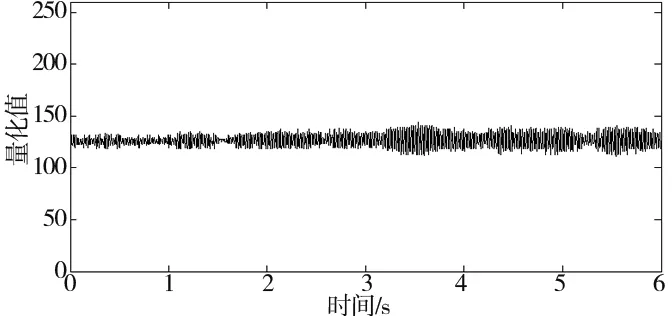
圖6 馬達振動數據野值修補結果圖

5 論文算法效率

在CPU為i7-7700、內存為8G的計算機上，用研究的一階差分算法與改進的均方誤差算法對液壓試驗臺數據進行野值判別與修補，每次處理算法迭代運行4次，耗時見表1所示，當數據量較大時，其高效性顯而易見。

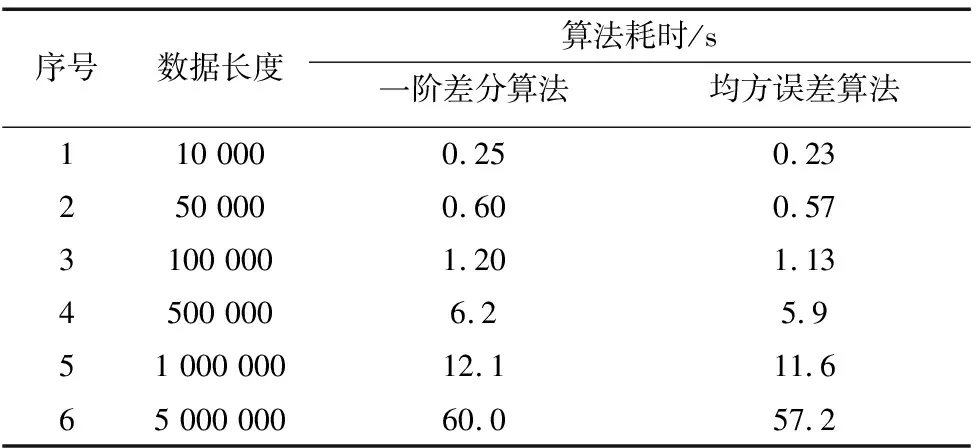
表1 野值判別與修補算法耗時

6 結束語

(1)測量數據中常常出現大量野值，研究提出的局部化處理模型可用于長數據序列野值的快速處理；

(2)研究了一階差分野值判別算法并應用到平穩信號數據處理，該類數據野值均被正確判別并得到了恰當修補；

(3)改進了均方誤差算法并應用到非平穩信號處理，局部處理細節顯示了算法在野值判別方面的有效性。