大導程螺母滾道型面數值分析與驗證*

邢永勝，歐 屹，梁 醫，王 凱

(南京理工大學機械工程學院，南京 210094)

0 引言

滾珠絲杠副作為機械設備中最常用的關鍵元件，能夠實現螺旋運動與直線運動的轉換，運動平穩且噪聲小，兼具可逆性好與效率高的優點[1]。進入21世紀后，滾珠絲杠副向著“速度”與“精度”兼顧的目標前進[2]，而增大導程是實現高速化的主要途徑。而大導程螺母內滾道的標準磨削加工過程中出現的螺母體與螺桿碰撞現象限制了其發展，因此在原有設備下，采取螺桿傾角小于滾道螺旋升角的干涉磨削方式進行內滾道加工[3]。

對于干涉磨削加工過程，Harada H指出，該方法中螺母體內表面與套筒軸的碰撞限制了螺母體長度，螺母滾道只能夠獲得部分完美的哥特式圓弧，砂輪與滾道的過度磨削現象導致剩余部分與理論型面產生較大偏離，卻并未分析過度磨削帶來的影響[4-5]。 Hegedus G對圓錐螺桿在螺母體內的空間位置進行了分析，依據套筒與螺母體的最小距離建立數學模型，分析了安全距離下不發生碰撞的螺桿長度[6]。范東風對比出了不同加工參數下，干涉加工獲得砂輪型面的差異，發現傾斜角度越大砂輪變得越尖銳，卻沒有分析與實際磨削量的聯系[7]。以上研究對磨桿碰撞問題進行了分析，未能獲得完整滾道型面。對于磨削過度問題，臺灣學者發現在特定情況下，根據嚙合原理計算的砂輪，不能加工出需要的螺紋型面，為此采用新的幾何方法計算砂輪廓形，同時調整砂輪傾角，來避免螺紋加工過程中的下切問題[8]。陶麗佳將磨削過度問題轉化為砂輪與理論螺桿轉子的干涉問題，進行了理論分析，利用ADAMS進行干涉校驗來證明螺桿鉆子磨削過程未發生過度磨削現象[9]。而實際加工過程中，過度磨削問題并不需要完全避免，保證良好的工作型面下，小區域的過磨削區域是可以接受的。

本文對干涉磨削加工下大導程螺母滾道型面，考慮存在較小過度磨削區域對磨削余量的影響，提出用動態法平面截取砂輪廓形計算最終滾道型面。建立誤差模型表征磨削余量增量，設計臨界角指標表征最終滾道是否符合設計要求，并分析了砂輪直徑、設計接觸角與磨削余量增量、臨界角的關系。

1 螺母內滾道磨削分析

1.1 螺母內滾道建模

螺母滾道法向截形為哥特式雙圓弧，根據已有的建模方法[4]，在母線坐標系O1-x1y1z1中，螺母滾道母線表達式：

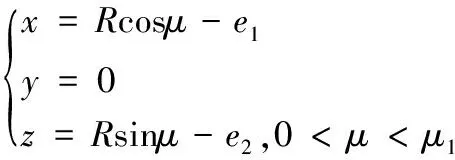
(1)

其中，R表示滾道半徑值，μ為法向截形相位角參變量，μ1=cos-1((R1-rm+e1)/R)，R1為大徑的二分之一，e1,e2為偏心距。建立單側螺母滾道表達式：

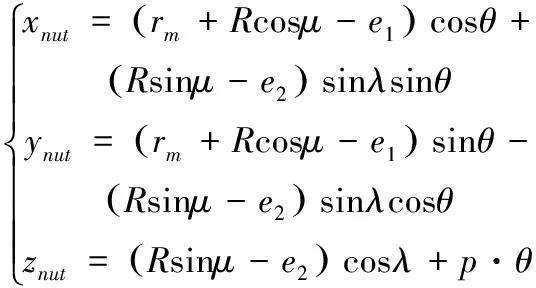
(2)

式中，θ為參變量，表示母線從起始繞z軸轉過的角度；rm表示公稱半徑，λ表示螺旋升角；p表示螺旋參數。內滾道干涉磨削與標準磨削圖如圖1所示。

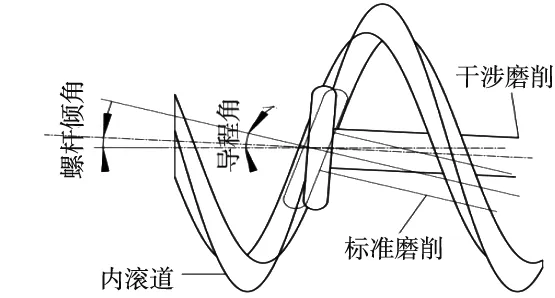
圖1 內滾道干涉磨削與標準磨削

建立砂輪與螺母的關系坐標系，如圖2所示。其中O-xyz是螺母坐標系，z軸沿軸線方向；O1-x1y1z1是螺母滾道法向型面即母線坐標系，兩坐標系中x1軸與x軸重合，原點O1與O點的距離為rm(公稱半徑)，y軸逆時針方向旋轉λ(螺旋升角)得到y1軸；O′-XYZ是砂輪坐標系，Z軸沿砂輪軸線方向，X軸與x軸重合，原點O′與O點的距離為a(中心距)，y軸逆時針方向旋轉Σ(砂輪偏轉傾角)得到Y軸。

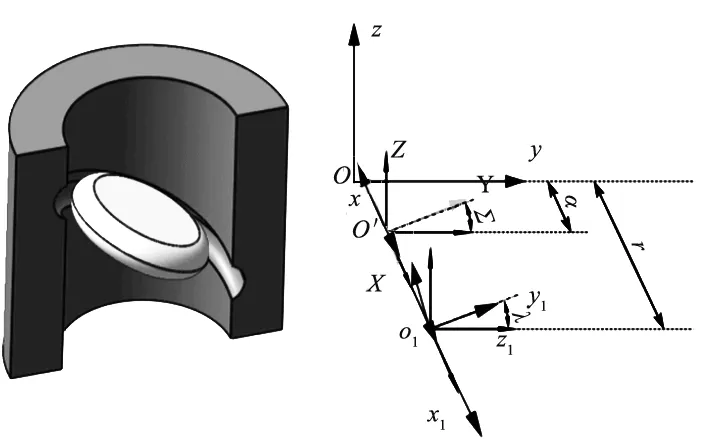
圖2 螺母滾道與砂輪坐標關系

則螺母螺旋面在砂輪坐標系O′-XYZ中的表達式為：

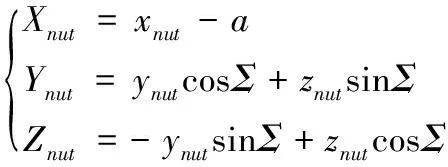
(3)

1.2 螺母滾道成形機理

根據一般的螺旋成形機理，根據坐標變換和嚙合原理，已知螺母滾道形狀或砂輪廓形其中之一，即可求解得到另一個。

如已知刀具廓型數據(Zt,Rt)在自身坐標系O′-XYZ中的表達式：

Xtool=Rtcosφ,Ytool=Rtsinφ,Ztool=Zt

(4)

式中，φ是參變量，它是半徑線R與平XO′Z面的夾角。根據接觸線條件式[7]方程(5)，可以得到磨削接觸點。將接觸點轉換到理論滾道型面的任一法平面下，可以得到滾道型面法向形狀。

f(Rt,Zt,φ)=nx(-RtsinφcosΣ+ZtsinΣ)+
ny(Rtcosφ+a)+pnz=0

(5)

仿真發現，基于式(5)的嚙合原理計算不能得到滾道最終型面。為此重新思考螺母滾道成形機理，為了簡化加工過程，假設螺母與砂輪處于加工接觸狀態，將加工過程離散為多個絕對靜止狀態，每個狀態不同之處在于砂輪與螺母滾道的相對位置。每一個絕對靜止狀態下砂輪都會對滾道進行磨削，此時滾道型面可認為是所有絕對靜止狀態下砂輪磨削產生的滾道型面的綜合。

理論上，理論滾道型面與廓形數據構成的砂輪在任何絕對靜止狀態下應該是處于恰好接觸狀態。然而，將理論螺母滾道與砂輪處于加工接觸狀態且絕對靜止，不考慮其他誤差，實際滾道型面相比于理論滾道型面產生誤差時，可認為是螺母理論滾道部分區域被砂輪廓形侵入造成的過度磨削現象。

2 滾道加工型面分析

2.1 動態法平面截取數值方法計算滾道型面

動態法平面截取法的中心思想與上文中簡化的螺母滾道成形過程一致，即滾道型面可認為是所有絕對靜止狀態下砂輪磨削產生的滾道型面的綜合。換言之，工件某處的滾道型面可以認為是多個絕對靜止接觸狀態下砂輪對該處所有作用的疊加。對滾道型面誤差判定的主要參照是理論滾道型面，因此建立理論滾道型面與砂輪廓形的加工接觸狀態圖。

圖3是動態法平面示意，圖3a是動態法平面原理的三維空間表述，圖3b是某法平面截取的理論滾道與砂輪型面。求參數為θ的理論滾道法向平面與砂輪的交點，而后利用坐標變換將交點轉換到理論滾道法向平面坐標系O2-x2y2z2下。參數為θ的理論滾道法向平面本質上為圖1中O1-x1y1z1螺母滾道母線坐標系沿著鋼球中心螺旋線旋轉角度θ得到的，即O1-x1y1z1坐標系中原點就是理論鋼球中心螺旋線上一點。由此可知，理論滾道與任何法平面的相交曲線皆為哥特式雙圓弧，與θ無關。

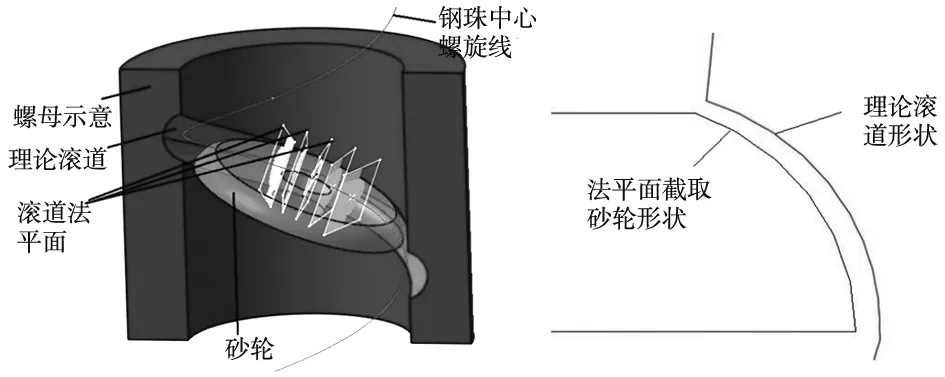
(a) 動態法平面 (b) 某法平面截取結果圖3 動態法平面法示意圖

采用空間平面的點法式方程建立工件坐標系下法平面。通過定點M(x0,y0,z0)，其法向量為n={A,B,C}的平面方程：

A(x-x0)+B(y-y0)+C(z-z0)=0

(6)

定點M采用螺旋線上鋼球中心點，與滾道建模時坐標系O2-x2y2z2類似，鋼球中心點的軌跡方程為：

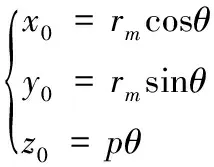
(7)

任一點的切向量為：

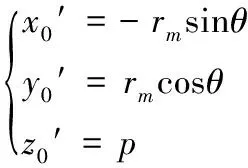
(8)

該切向量就是過M點滾道法向平面的法向量n={A,B,C}。將式(7)、式(8)帶入式(6)，得到法向平面的方程式(9)：

f(x,y,z,θ)=x0′(x-x0)+y0′(y-y0)+z0′(z-z0)

(9)

聯列法向平面的方程(9)與工件坐標系下砂輪表達式，人為設定參數θ步長，然后將砂輪廓形數據代入，即可得到工件坐標系中一系列參數θi的法平面與砂輪的交點。根據坐標變換將法平面與砂輪的交點分別變換到相同參數θ的動態法平面坐標系O2-x2y2z2中，得到各自法平面下的離散點沿y2軸方向的分量皆為0，與螺母滾道母線坐標系O1-x1y1z1下母線表達式(1)對應。

2.2 數據處理與誤差模型建立

在母線坐標系O1-x1y1z1中，將所有計算結果與滾道母線分別表示如圖4所示。采用相位區間篩選方法獲得第一象限內邊緣數據作為滾道形狀，如圖5所示。

圖4 動態法平面截取到的砂輪廓形包絡曲線簇 圖5 相位區間篩選數據原理

改進誤差模型[8]，實際型面離散數據集的一階導數采用差分法后精度高且易求，計算出任意點的法線與理論曲線的交點，然后求二者距離作為廓形誤差。如圖6所示，圓弧部分代表理想滾道型面，它的函數方程式已知的。B(xi1,zi1)、C(xi2,zi2)、D(xi3,zi3)三點為實際型面數據，根據C、D點可以求得B點切線斜率k，再求得B點法線斜率，聯立法線表達式與圓弧方程求得交點B′(xi4,zi4)，則BB′點距離可以求得。

過B點的法線直線可表示為：

(10)

故型面誤差為：

(11)

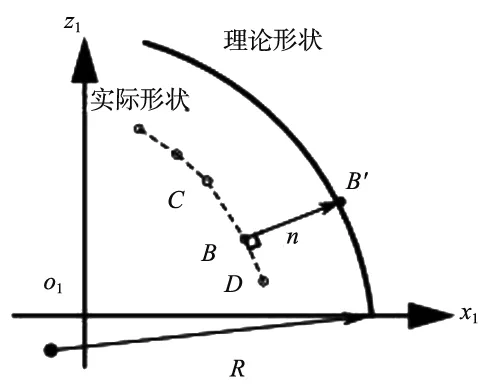
圖6 誤差模型示意

同時引入整體誤差Ε作為評價指標：

(12)

式中，N為實際型面上過度磨削區域離散點個數。整體誤差Ε用于表征磨削余量增量，增量大會加速砂輪磨損，單工序中砂輪修整次數增多。

臨界角指標指計算參數接觸角α應該小于完美哥特式弧形的臨界角度αc，并留有一定安全值，如圖7所示。故干涉加工下螺母滾道過度磨削區域采用整體誤差E評價，在加工過程中比非過度磨削區域需要更多的加工余量，完美哥特式弧形區域的大小采用臨界角度αc評價，決定最終滾道是否合格。

圖7 臨界角示意

2.3 滾道干涉原理分析

大導程螺母滾道的過度磨削現象與砂輪的廓形有關，在接觸狀態下砂輪將侵入理論螺母滾道。根據成形機理[9]，在加工過程中破壞螺旋面形成線，滾道會產生型面偏差。因此將螺母理論滾道置于砂輪坐標系式(3)，用平行于XOY平面的面去截取滾道，得到任一砂輪廓形下與滾道相交曲線，查看該平面中砂輪半徑Ri與相交曲線的位置關系。

圖8a為平行于坐標系XOY且平面參數為Z的平面與螺母理論滾道型面的相交情況，根據式(4)紅色虛線為該平面下的砂輪圓，由圖8b可以看出二者可能存在兩個相交區域，曲線之間相切相交區域，和滾道邊緣與砂輪圓的相交區域。而第二個相交區域就是造成滾道過度磨削的主要原因，從數學角度上來解釋，就是該相交曲線上存在到砂輪軸距離小于砂輪圓的部分。因此砂輪直徑會影響到滾道弧形的臨界角度αc，即影響過度磨削程度。

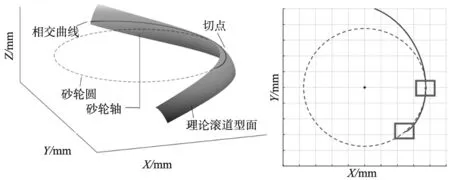
(a) 任一砂輪圓與相交曲線的空間示意 (b) 砂輪圓與相交曲線的二維示意圖8 砂輪圓與相交曲線的關系

3 滾道型面仿真與試驗驗證

以某型號的螺母為例進行仿真計算，參數如表1所示。

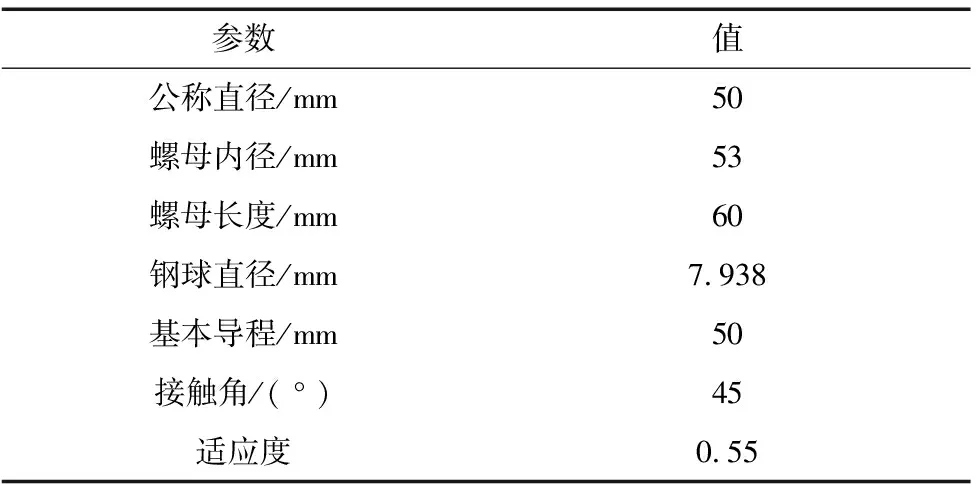
表1 某型號螺母參數

3.1 螺母滾道過度磨削程度與砂輪直徑的關系

由于螺桿傾角與砂輪直徑、螺母長度存在一定的關系[5]，而螺母直徑需大于磨桿外徑，小于螺母內徑，在此范圍內設置對比試驗研究過度磨削程度與砂輪直徑的關系。

預設參數分為兩部分，第一部分為三組螺桿傾角與砂輪直徑的較優組合，第二部分為三組0°螺桿傾角與不同砂輪直徑分別組合。

表2 螺桿傾角、砂輪直徑對臨界角度、整體誤差影響

第一部分預設參數下，螺桿傾角與砂輪直徑同時發生變化，臨界角度αc增大，砂輪直徑總變化值為10 mm，臨界角從61°變為67°(最大值)，整體誤差值E保持較小值，滾道過度磨削現象趨于消失。

第二部分預設參數下，單獨減小砂輪直徑也可以增大臨界角，砂輪直徑從35 mm變化到25 mm過程中，砂輪直徑總變化同樣為10 mm，臨界角增大幅度達20°左右，遠遠滿足設計要求，整體誤差從8 μm減小為3 μm，同樣表明過度磨削區域的大幅縮減。結合圖9可以看出，得到的滾道法向截形更接近理論值。

對于滾道磨削加工過程，較小的磨桿傾角意味著磨桿與螺母體發生碰撞干涉的幾率小，但實際磨削量增加導致磨削效率低。而較大的磨桿傾角實際磨削量小，砂輪磨削效率高，且不易磨損。

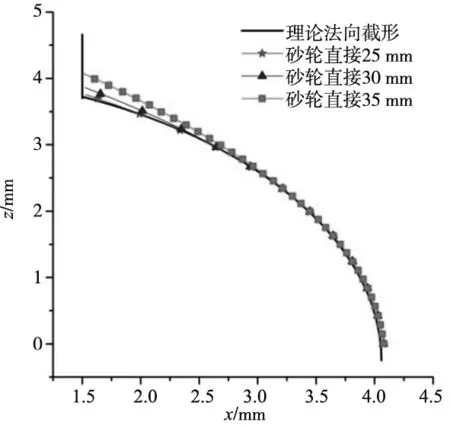
圖9 螺桿傾角0°下不同砂輪直徑磨削后滾道法向截形

3.2 螺母滾道過度磨削程度與設計接觸角的關系

合格螺母滾道的臨界角αc需要大于設計接觸角α，螺母設計接觸角一般小于絲杠接觸角3°左右[13]，可以減小空回程角。設計對比試驗，螺桿傾角0°，砂輪直徑30 mm，改變設計接觸角α研究臨界角αc的變化。

如表3所示，等幅減小設計接觸角，臨界角以較小幅度增加，可認為間接滿足了設計要求。考慮到實際接觸角相對于設計值存在一定的上下浮動，當臨界角比實際接觸角微大時，認為不滿足設計要求。

表3 接觸角對臨界角度影響

3.3 試驗驗證

不同程度的過度磨削引起的磨削增量難以直接驗證，卻可通過良好磨削工況下工序中砂輪修整次數間接表示。考慮到操作可能導致的螺桿與螺母碰撞與實際修整次數本身存在彈性量，采用螺桿傾角0°，分別取直徑為35 mm與25 mm的砂輪進行內螺紋滾道磨削。如圖10所示，內螺紋磨床型號為漢江SK7620A，磨削工藝為粗磨與精磨，進給量為0.02 mm。

如表4所示，不同過度磨削程度會影響到砂輪修整次數。砂輪直徑從35 mm替換為25 mm，良好磨削工況下砂輪單次工序修整次數從5次變為2次，表明實際磨削量的減小與加工效率的提升。通過測量兩個工件的實際臨界角，考慮測量誤差下實際臨界角均處于表2中的仿真誤差允許范圍內。

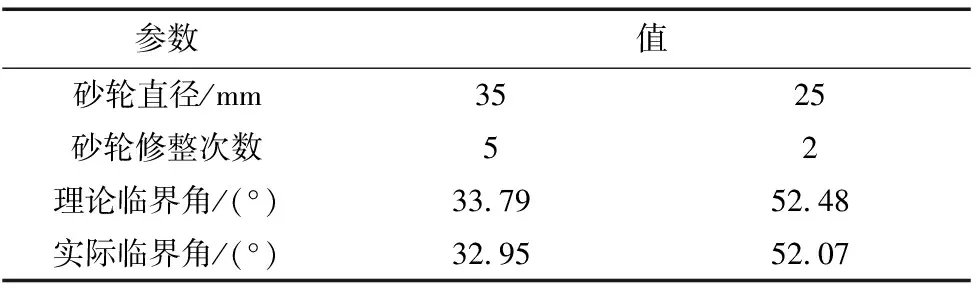
表4 不同砂輪直徑對臨界角影響

圖10 7620A磨床干涉磨削螺母過程

4 結論

根據螺母滾道建模與砂輪聯合計算，得到螺母滾道干涉誤差模型，通過實例仿真分析，得出以下結論：

(1)大導程螺母滾道完整形狀可以通過滾道多個法向平面截取砂輪廓形得到，干涉加工容易發生滾道過度磨削現象，是由于某一砂輪圓平面與滾道的交線存在兩處相交區域。

(2)通過增大砂輪直徑可以增大加工滾道圓弧的臨界角，滿足滾道設計要求，但需與螺桿傾角匹配，保證磨削效率。改變設計接觸角，可以間接滿足接觸角設計要求。

(3)誤差模型中整體誤差E可表征滾道過度磨削引起的磨削余量增量，不同程度過度磨削現象引起的磨削增量變化可通過穩定磨削工況下砂輪修整次數差異間接驗證。