菱形負剛度機構HSLDS隔振器優化設計研究

袁屹杰，紀 明，張衛國，王 譚

（西安應用光學研究所，陜西 西安 710065）

1 引言

由正、負剛度效應器件并聯構成的隔振器，是HSLDS隔振器的主要形式，其中負剛度效應器件是決定隔振非線性的關鍵因素，為了獲得更好的隔振性能，已發展出種類豐富的負剛度構型[1-5]。相關研究[5-6]表明，合理地增加隔振器非線性調節參數，可以較靈活地改善隔振性能。但在工程應用中，較豐富的調節參數，通常會增加設計難度：各參數間需要進行匹配優化，否則可能導致相反的結果。現有的研究多數僅從理論層面分析隔振器相關參數單獨對隔振性能的影響關系，文獻[7]將遺傳算法引入到準零剛度隔振器優化設計中，以剛度非線性作為優化目標函數，對隔振器的相關參數進行整體優化，取得了較好的效果。但仍存在一定局限性，如：針對非線性參數的單目標優化方法，無法滿足非準零剛度狀態的HSLDS隔振器優化應用需求；同時，在工程優化設計中，受結構、材料參數限制及彈性器件規格不連續的影響，容易導致種群目標空間分布不均勻，采用經典遺傳算法，存在局部目標空間搜索效率低下的問題。

針對提升非線性隔振性能并實現工程優化設計的需求，基于一種非線性調節能力較強且結構相對緊湊的菱形連桿負剛度機構，提出了具體的HSLDS隔振器實現方案，并提出了以隔振性能與負剛度機構質量為目標函數的多參數優化模型，將不連續因素納入優化分析中。采用目標空間分區域搜索的NSGA-Ⅱ多目標遺傳算法，獲得隔振器參數Pareto最優解集；利用仿真方法對參數選擇進行分析，并采用實物樣機對結果進行驗證。為菱形HSLDS隔振器工程優化、應用探索一條可行的技術途徑。

2 隔振器分析建模

2.1 隔振器模型

菱形HSLDS隔振器方案，如圖1所示。包含四個菱形負剛度機構，每個菱形負剛度機構由兩組菱形連桿通過四根軸并聯組成，各鉸接軸處均可以靈活轉動，其中，一組呈對角關系的鉸接軸分別連接振動基座與隔振平臺，另一組鉸接軸分別連接拉簧的兩端，拉簧處于拉伸狀態時，菱形連桿機構具備負剛度特性。

圖1 菱形HSLDS隔振器模型Fig.1 Rhombus HSLDS-VI Model

菱形HSLDS隔振器原理圖，如圖2所示。以振動基座與隔振平臺間負剛度機構支點的水平距離L為基準尺寸，令：----AB=ɑL、----BC=bL、H=hL；H=0時，隔振器處于平衡位置，此時拉簧拉伸量為C=cL。為簡化分析，令ɑ≥b。主隔振器的剛度為Kp=K，阻尼系數為Cp；拉簧的剛度為Kn=eK。

圖2 隔振器原理圖Fig.2 Illustrative Diagram of Isolator

令拉簧對B點的力為f，則沿----AC方向產生的合力F為：

式中：f0—拉簧的初始拉力。

F在振動方向的作用力為：

聯立式（1）、式（3）、式（4），得到菱形負剛度機構沿平臺振動方向的彈性力，結合主隔振器彈性力因素，隔振裝置的等效彈性力為：

2.2 優化評價參數

忽略拉簧阻尼影響，菱形HSLDS隔振器的等效剛度與主隔振器阻尼是影響隔振性能的主要因素，其中，等效剛度包含兩個影響參數。

其一是零位剛度，零位剛度為隔振器等效無量綱剛度的最小值，隔振器主要工作于平衡位置、即零位剛度附近區域，零位剛度很大程度上決定著隔振器的隔振性能。一般情況下，零位剛度越小，隔振性能越好。

依據幾何關系，平衡位置處負剛度機構拉簧的變形量C0滿足式（7）。

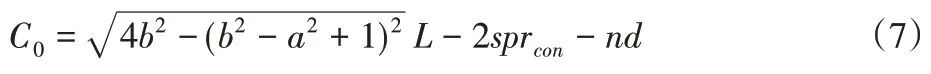
式中：sprcon—拉簧有效段兩端與鉸接軸間連接段的長度；n—拉簧有效段的圈數；d—拉簧的線徑。

由式（6）與式（7）可得：

此外，還需要考慮剛度非線性因素對隔振的影響，如圖3所示。雖然剛度曲線1與曲線2的零位剛度一致，當振動相對位移h超過一定范圍時，曲線1對應的剛度數值將超過曲線2所對應的剛度。因此，需將剛度的非線性也作為隔振性能評價參數。

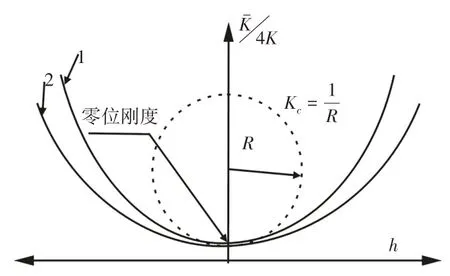
圖3 隔振性能評價參數示意圖Fig.3 Diagram of Vibration Isolation Performance Evaluation Parameters

目前，還沒有廣泛采用的剛度非線性量化評價方法，文獻[7]將剛度小于某一數值所對應的相對位移區間寬度作為非線性評價參數，但在實際應用中，非線性的變化通常難以預估，導致參考數值的選取存在一定隨意性。由于隔振平臺的相對位移主要是在平衡位置附近區域，而剛度曲線在平衡位置處的曲率可以較好地反映平衡位置附近區域的剛度非線性變化趨勢。因此，可采用剛度曲線在平衡位置點處的曲率Kc，即零位曲率，作為剛度非線性的量化評價參數。一般情況下，零位曲率Kc值越小，剛度曲線在平衡位置附近越平直，隔振性能越好。根據定義有：

除隔振性能外，HSLDS隔振器引入負剛度機構所產生的額外質量也需要納入評估范疇，特別是在一些對質量較敏感的應用中。菱形HSLDS隔振器的負剛度機構由連桿、軸及拉簧構成，在參數選擇階段，可將連桿、拉簧參數作為優化分析變量。令質量評價參數為Sf：

式中：η—連桿質量因子；d、D、n、ρ—拉簧的線徑、直徑、有效圈數及材料密度。

3 優化分析算法

菱形HSLDS隔振器優化模型涉及三個優化量，需采用多目標遺傳算法（MOGA）進行優化。NSGA-Ⅱ算法[8]采用快速非支配排序與擁擠度排序算法，將父代與子代合并處理，保留了所有精英個體，具備較高的優化效率，是目前廣泛應用的MOGA算法。

在優化分析中，為使分析貼近工程應用，設定負剛度機構拉簧的線徑d與直徑D參數符合標準[9]。由于拉簧參數不連續，同時受幾何參數以及材料極限應力限制，有效參數的分布并不是連續、均勻的。經典NSGA-Ⅱ算法的下一代個體選擇機制，并未考慮級別靠前的非支配層中精英個體分布的均勻性，若直接應用于本分析，將導致Pareto前沿搜索效率存在顯著的區域性差異。針對此問題，采用文獻[10]提出的目標空間分區域優化、搜索策略，即將目標區域分為若干個子區域，每個子區域單獨地進行遺傳運算，確保目標空間各區域獲得相似的搜索效率。

3.1 區間劃分方法

菱形HSLDS隔振器Pareto最優解在目標空間中分布并不具備對稱屬性，文獻[10]中所介紹的超球面分區方法，難以較均勻地分割解的分布空間。考慮到三個目標函數的關重差異性，可以采用降維的分區方法：以表征隔振性能的兩維數據進行目標空間劃分，如圖4所示。在一個空間象限中，依據角度，i等分歸一化數據所構成的平面象限，并以平面角度將空間象限等分為i個子空間：Q1～Qi。子空間數目可根據數據分布情況確定，本應用中選用6子空間劃分。

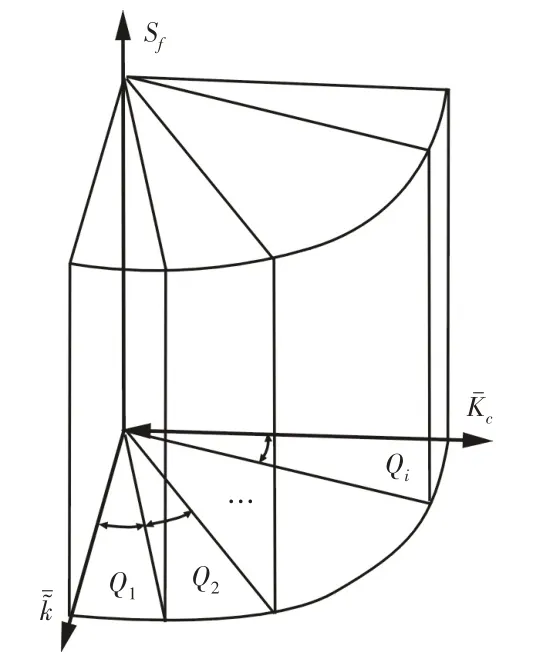
圖4 目標空間分區示意圖Fig.4 Diagram of Object Space Partition

3.2 分區遺傳算法

第一步，數據初始化，設定總初始種群數N，并根據子區域數進行等分，使每個子區域內的種群個體數目一致。

第二步，每個子區域種群內部進行交叉、變異；對每個子區域i，隨機產生數量為當前子種群數ni的20%的全局新個體，并隨機挑選子區域i內的個體，與新產生的全局個體進行交叉處理。

第三步，對所有新產生的個體進行分區，與各子區域原有的個體合并，組成新的子區域種群。

第四步，對各子區域種群分別進行非支配排序，挑選優秀個體作為下一代種群個體。挑選一下代個體過程中，存在三種情況：

（1）子區域中的非支配個體數小于子區域初始個體數。

（2）子區域中的非支配個體數不小于子區域初始個體數，且第一級非支配層個體數不大于子區域初始個體數。

（3）子區域中第一級非支配層個體數大于子區域初始個體數。

①第1種情況，多出現于初始階段計算中，處理方法是：隨機產生新個體，保證該子區域內的有效個體數不少于初始個體數。

②第2種情況，處理方法與經典NSGA-Ⅱ算法一致。

③第3種情況，當該子區域內第一級非支配層個體數不大于2N時，保留第一級非支配層的所有個體；當第一級非支配層個體數大于2N時，則對個體進行擁擠度排序，挑選間距較大的2N個第一級非支配層個體進入下一代，避免計算規模過大。

第五步，遺傳代數如未達到指定代數，轉入第二步，否則輸出當前代數據。

算法采用實數編碼方式，交叉處理采用正態交叉算子[11]，交叉概率為0.9；變異處理采用多項式變異算子[12]，變異概率為0.1。

4 優化分析算例

某應用，隔振負載為12kg，在該負載作用下，主隔振器的諧振頻率13Hz，隔振平臺最大相對位移≥12mm。拉簧參數選用標準[9]附例中的公式計算，設定拉簧為碳素彈簧鋼材質，材料的切變模量G=7.9×104MPa，初始拉力f0=0。

初始方案參數，如表1所示。

表1 初始方案參數Tab.1 Initial Parameters

對上述應用進行參數優化分析，優化數學模型，如式（11）所示。拉簧選擇標準[9]中線徑為(3～5)mm對應的所有型號，拉簧有效段圈數n的步進調節量為0.5圈；連桿采用鋁合金材料，根據形狀設定質量因子η=0.7g/mm。

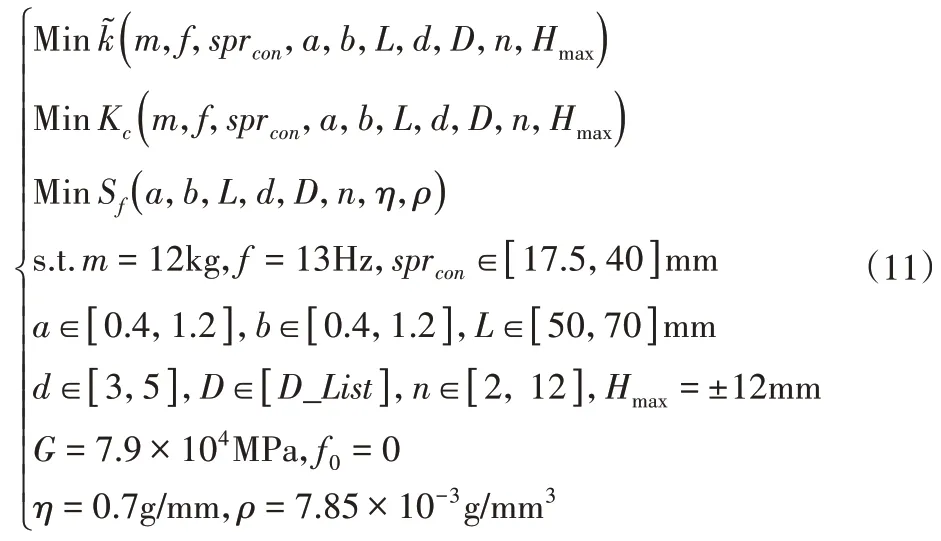
設定總初始種群數N=300，經過300 代計算后得到Pareto最優解集，如圖5所示。

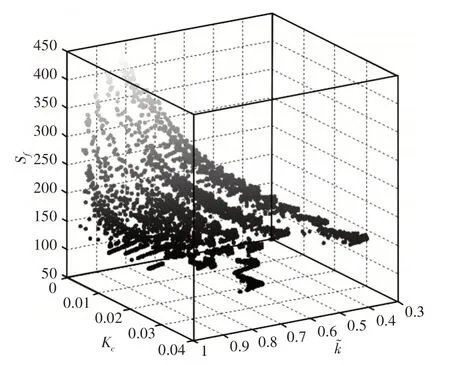
圖5 Pareto最優解圖示Fig.5 Diagram of Pareto Optimal Solutions

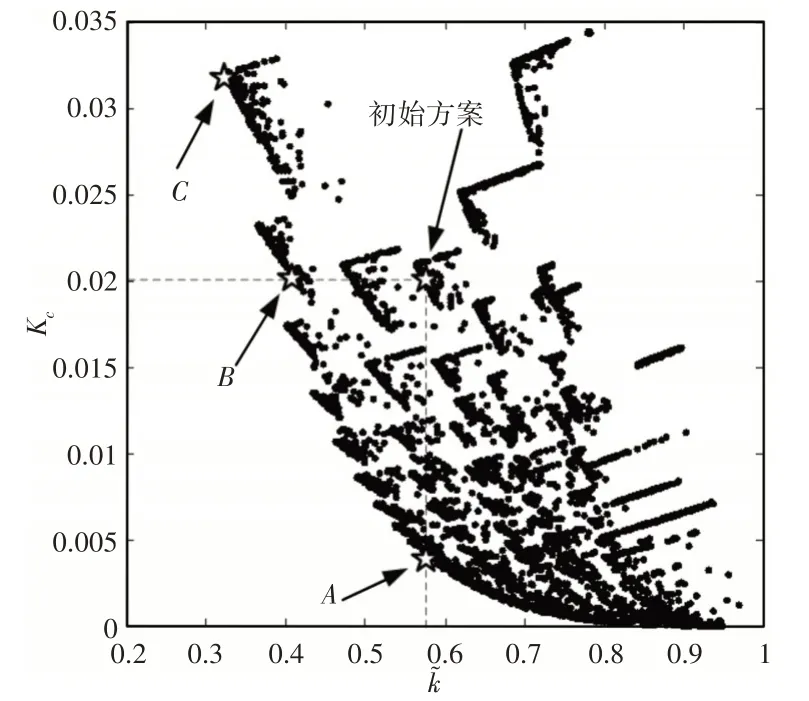
圖6 Par eto最優解-Kc平面投影圖Fig.6 Pareto Optimal Solutions Projection on -Kc Plan e

5 參數選擇分析

獲得Pareto最優解集后，需要從中選擇一個可以應用于工程設計的參數。為確定參數選擇策略，在Pareto最優解中選取三個有代表性的參數點，如圖6、表2所示。其中，A點的及B點的Kc分別與初始方案對應的數據相等，C點為Pareto最優解中最小的數據點。

表2 Pareto最優解數據Tab.2 Pareto Optimal Solutions Data

采用MSC.ADAMS 軟件對上述參數的隔振性能進行分析。鑒于HSLDS隔振器的非線性特征，分析方法是：將諧波振動施加于振動基座，采集振幅穩定后、一段時間內的隔振平臺位移量值，對數據進行均方根處理，得到隔振輸出，并以絕對位移傳遞率作為隔振性能評價參數。

設定主隔振器阻尼為0.19N.s/mm，輸入擾動加速度幅值為1.4g，對多頻點進行采樣，得到隔振器位移傳遞率圖譜，如圖7所示。諧振點參數，如表3所示。從中不難看出，Pareto最優解集中A、B、C三組方案對應的隔振性能均優于初始方案，其中方案C，零位剛度最小，隔振優化效果最佳，說明零位剛度在兩種隔振性能評價參數中起主導作用；在相同零位剛度條件下，較小的零位曲率可以獲得更好的隔振性能，方案A與初始方案參數曲線，如圖7所示。

圖7 隔振器位移傳遞率圖Fig.7 Isolator Displacement Transfer Rate Diagram

6 實驗驗證

實驗采用等效方式進行：隔振載荷為6kg，主隔振器與有效負剛度機構數量均縮減為2個且對稱分布，另一對不含拉簧的菱形連桿機構，起約束運動、實現無角位移垂向隔振的作用。實驗平臺，如圖8所示。加速度幅值為1.4g的掃頻曲線，如圖9所示。其中ɑ、b、c、d、e分別對應主隔振器、初始方案、方案A、方案B以及方案C的掃頻數據，諧振點參數，如表3所示。

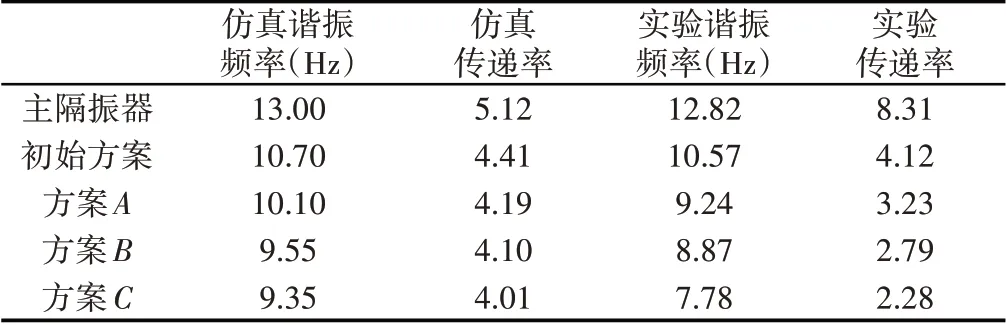
表3 諧振點參數Tab.3 Resonance Point Parameters

圖8 隔振實驗平臺Fig.8 Vibration Isolation Experimental Platform

圖9 掃頻位移傳遞率曲線Fig.9 Displacement Transfer Rate Curves of Sweep Frequency Vibration

諧振頻率的實驗與仿真數據吻合得較好。諧振頻率實驗數據小于仿真數據是由兩部分因素導致的：（1）拉簧存在一定初始應力，使實際零位剛度小于計算數據；（2）負剛度機構質量對隔振存在影響。初始方案至方案A、B、C的傳遞率實驗數據對比仿真數據依次降低，說明隨著負剛度拉簧力的增加，負剛度機構的內部摩擦力對隔振影響逐漸顯著，相關內容將在后續論文中進行討論。

7 結論

分區搜索的NSGA-Ⅱ算法，可以有效應用于參數不連續、分布不均的多參數優化問題，較好地獲得菱形HSLDS隔振器參數的Pareto最優解集；采用動力學仿真方法對最優隔振參數的選擇進行分析，并以實物樣機驗證了所提方法的有效性。得出以下結論：在表征隔振性能的兩參數中，零位剛度起主導作用，零位剛度越小，或零位剛度一致情況時，零位曲率越小，隔振器低頻段隔振性能越好；同時，選擇較小零位剛度，可兼顧降低負剛度機構所產生的附加質量。

所提出的分析方法，不僅可應用于菱形HSLDS隔振器設計優化，對其他類似非線性隔振器的工程設計及優化也較好的參考價值。