如何將笛卡兒思想融入高中平面解析幾何課堂

侯代忠 蘇元美

[摘? ?要]在新課程理念下，平面解析幾何教學應認真挖掘知識背后的數學文化，發展學生數學思維.笛卡兒作為解析幾何的創始者，其思路、思想與方法對現代的解析幾何影響深遠，更是值得我們挖掘.

[關鍵詞]數學思想;笛卡兒;曲線與方程;課堂教學

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2021）17-0014-03

新課程理念下的數學教育，要在數學本質的基礎上賦予課堂新的生命力，強調在課堂上發揚數學文化，傳承數學精神.教育家米山國藏說過：隨著時間的流逝，僵硬的數學知識點與定理會淡忘在人們的腦中，但是在接受數學過程中產生的數學思想、數學方法、數學思維、數學精神和數學情感等會伴隨人們一生，并能夠將其運用到其他領域中.

解析幾何知識作為高中數學的重要組成之一，在高考中也占有著舉足輕重的地位，是學生的重點學習板塊.解析幾何的知識中包含著許多數學思想，也承載了許多歷史.了解解析幾何的發展史對我們的幾何學習有重要的作用.

《求曲線的方程》作為解析幾何的起始內容，在教學中教師常常讓學生生搬硬套解題的步驟，不過多解釋緣由，從而忽略了一些能很好地滲透數學思想、數學素養、數學情感的好課.本文談談如何將笛卡兒思想融入高中平面解析幾何課堂.

一、笛卡兒的解析幾何思路

法國著名數學家笛卡兒是解析幾何的創始人之一.在笛卡兒創立解析幾何之前，幾何和代數這兩個學科早已獨立發展起來了，但是卻沒有交集.當時笛卡兒認為，歐幾里得幾何太過于依賴圖形，在證明過程中過分強調技巧性，過于抽象，對于想象力的要求較高;代數學卻是單純的計算，機械地進行法則和公式的運用，過于死板，不利于思維的發展.

笛卡兒看到了幾何的直觀性與代數的簡便性，他結合了兩種領域的優勢，創造性地把幾何和代數結合起來，也就是“數形結合”思想.此后，數學進入了變量數學階段，開辟了變量數學，為今后的黎曼幾何奠定了基礎.笛卡兒曾說過：“我要改革這個局面，把抽象的幾何，變成那些不需要去思考太多幾何邏輯僅用于練習思想的問題，這樣做也是為了更好地研究幾何.”

笛卡兒解析幾何的基本思路包括：

（1）引入坐標觀念，指出平面上的點和實數對（x，y）的對應關系;

（2）利用坐標法，加入極限思想.坐標上的點都可以表示成一個數，當無數個數連接到一起時，便形成了一條曲線，這樣就可以用方程去表示曲線;

（3）提出了用方程關系表示曲線的思想，具有同種關系的點，就可用一個方程表示;

（4）找到圖形中已知幾何圖形與未知幾何圖形之間的等量關系，將其用代數形式表示，用已知的量表示未知的量，構造代數方程;

（5）最后通過代數法則求解方程，最終解決幾何問題.

研究笛卡兒創立解析幾何的歷程，我們可以得到：數學思想——數形結合、特殊到一般;數學方法——變量代替不變量;數學原理——映射原理.

二、《求曲線的方程》中蘊含的解析幾何因素

曲線和方程是解析幾何中的核心概念.研究曲線與方程的目的是用代數的形式表示曲線的幾何特征，并通過代數運算法則處理相關的等量關系，進而利用代數法則去求解，從代數的結論得出相應的幾何性質.學會求曲線的方程是研究幾何性質的基礎與關鍵，即利用映射原理，將曲線上的點與方程上的解一一對應.曲線上的所有點構成集合，也就是一個方程.“數形結合”與“由特殊到一般”等是整個解析幾何的重要數學思想.

目前的教學與學習上側重于機械的算法訓練，忽視了很多幾何的特征.笛卡兒創立的對幾何簡約處理的解析幾何，現代學生并沒有感受到其科學價值與文化地位.一味的機械計算，又偏離了高中解析幾何的課標指引，同時也違背了笛卡兒創立的初衷.

本節通過笛卡兒思想由來的滲透，體會數學的本質，加深學生對數學中的代數方法的認識，鞏固求曲線的方程步驟的應用，感悟數學思想.

三、將笛卡兒思想融入解析幾何課堂的策略

1.挖掘知識深度

每個知識點的背后都隱藏著獨有的思想方法與邏輯思維，而這個知識的歷史是數學發展過程的記錄，記載了知識的發生和經過，記載了數學家研究成功與失敗的過程，其中蘊含著數學思想的傳遞及數學思維的形成.

歷史的研究主要是研究人類的思想，從歷史的認識方法論的特征中我們可以了解到，想要研究歷史，并不是單純地了解歷史，而是從歷史的起點出發，以整體的大觀去理解歷史，研究其歷史思想，并與現實社會結合到一起，在此基礎上“再創造”出新的成果.

教師在備課過程中，要對教材進行深入的研究，抓住知識的本質，積極挖掘知識背后的數學文化、思想產生過程.重新整理數學歷史材料，提煉出其思想方法，與數學知識結合在一起，為課堂教學做好充分的準備.

課前可以做以下步驟：

（1）挖掘.可以從歷史中挖掘出數學邏輯思維、思想方法的文化內涵.

（2）轉化.將歷史素材轉為數學材料，研究解析幾何的教學策略.

（3）聯系.將課堂及現實社會聯系起來.

例如，高中解析幾何就是笛卡兒所創立的解析幾何，教師在準備這個章節時可以從笛卡兒的創立的心境、環境、思維過程、思想方法和克服困難等去進行課堂各方面的滲透.

2.拓展知識廣度

知識的數學史材料包含著知識的思想方法，將數學思想融入課堂的途徑可以參考數學史融入數學課堂的途徑，使得課堂有趣、豐富起來，讓學生在“再經歷”的過程中，培養學生的創造性思維能力，同時還能學習數學家刻苦鉆研的精神.

對于將數學史材料滲透到數學課堂中，汪曉勤提出了四種方法：附加式、復制式、順應式、重構式.附加式與復制式是直接應用，較為簡單.而順應式與重構式則是較為高級的滲透方式.重構則是“再創造”知識發生的過程，讓學生置身于知識產生的過程，去感悟思想的形成與方法的建構，體會科學家在探索過程中的困難，再感受解決困難時思想發生的過程.

教師可根據不同的課型，選擇適當的方式進行教學.

例如，以一個實際問題開啟課堂.有一個半徑是1米的圓形鐵圈，有一根木棍連著圓上的一個動點和距離圓外3米的點，有一只老鼠在木棍上的中點，求老鼠移動的軌跡.

用一個實際題目，設置困難，幻想自己是笛卡兒，如何去解決這個困難？

引導學生思考：老鼠移動的軌跡，就是老鼠的各個腳步匯聚起來的點.將老鼠的各個腳步看成一些點，這些點的集合就是一條線.那么怎么去找到這樣的一條線呢？這樣的一個中點怎么可以和前面的信息搭建起聯系呢？

教師可以切換回歷史，當時的笛卡兒和大家也有一樣的困擾，這樣的問題用純幾何的方法去解決，難度似乎有點大.他為了使問題解決得更快捷，為了能夠表示這樣的位置，創造出了“笛卡兒坐標系”.他將幾何圖形搬到“笛卡兒坐標系”中，將“數”與“形”完美地結合在了一起.我們來看看題目有了怎么樣的變化？

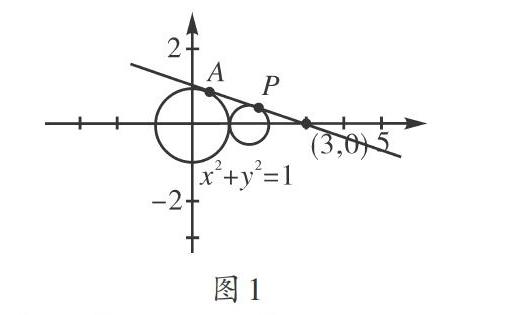
如圖1，動點A在圓[x2+y2=1]上移動時，它與定點（3，0）的連線的中點P的軌跡方程是什么？

在這里引導學生用代數的經驗去完成題目，進行總結，并展示笛卡兒的思路，進行對比，去感受笛卡兒的解析幾何給我們現代生活帶來的便利，并學習笛卡兒的創新精神.

3.提升知識高度

在教學之后，教師可升華課堂知識，將知識的傳授提升到思想方法的滲透，將理性課堂提升到人文情懷的境界，將知識的學習提升到傳承數學精神的層次.教師要善于發現與總結，要將課堂與數學材料的人文情懷與數學精神結合到一起，引導學生從理性思考跨越到感性精神上.

例如，在《求曲線的方程》的課程結尾，可以以下一段話總結，提升課堂的高度.

在今天的這一堂課里，我們“再次經歷”了當年笛卡兒的經歷，也遇到了同樣的困難;我們感受到了數學家的數學思想，感受到了他們的奮斗精神.雖然我們不能完完全全重走他們當年的道路，但是思想能夠產生思想，精神能夠影響精神.因此，我們要從他的思想中汲取有價值的營養，融入我們新的思路，我們要站在巨人的肩膀上，再創輝煌！

處于現代社會的我們不可能完完全全重走數學家所經過的路程，但是我們也不能因此冷凍歷史，而應該讓歷史鮮活起來，汲取其中的精華.教師作為教育的領路人，應注重在課堂中滲透數學文化，讓學生在感受知識的創造過程中，促進思維的發展，領悟數學精神.

[? ?參? ?考? ?文? ?獻? ?]

[1]? 中華人民共和國教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018.

[2]? 楊懿荔.從數學史視角探究“曲線與方程”教學難點的成因及克服策略[J].上海中學數學，2018（5）：3-7.

[3]? 李鐵安. 基于笛卡兒數學思想的高中解析幾何教學策略研究[D].重慶：西南大學，2007.

[4]? 宋欣然. 新課標下高中平面解析幾何教學策略研究[D].延吉：延邊大學，2019.

[5]? 國佳.高中新課程“數學史選講”應講些什么：以平面解析幾何產生為例[J].中學數學雜志，2008（7）：14-15.

[6]? 徐德明. 高中解析幾何知識中數學思想方法的教學策略研究[D].哈爾濱：哈爾濱師范大學，2019.

[7]? 丁彬.數學史的方法與中學數學教學的融合[J].數學學習與研究，2019（2）：61-62.

[8]? 王環. 數學史融入初中數學教學現狀及策略研究[D].信陽：信陽師范學院，2019.

[9]? 許苗.數學史與初中數學新課引入的應用[J].數學學習與研究，2018（3）：63.

[10]? M.克萊因.西方文化中的數學[M].上海：復旦大學出版社，2004.

（責任編輯 黃桂堅）