借助數(shù)學(xué)文化　滲透數(shù)形結(jié)合思想

韓茂芳

【摘要】勾股定理被稱為“幾何學(xué)的基石”，它揭示了直角三角形三邊之間的數(shù)量關(guān)系，體現(xiàn)了“數(shù)”與“形”的互相轉(zhuǎn)換，表明了數(shù)形結(jié)合思想在數(shù)學(xué)教學(xué)中有不可忽視的作用。基于此，本文探討了如何在“勾股定理”教學(xué)的各個環(huán)節(jié)滲透數(shù)形結(jié)合思想，旨在為中學(xué)數(shù)學(xué)教師的教學(xué)提供一些新的視角。

【關(guān)鍵詞】數(shù)形結(jié)合思想;勾股定理;教學(xué)設(shè)計(jì)

“數(shù)”與“形”是數(shù)學(xué)知識的兩種表現(xiàn)形式，“數(shù)”體現(xiàn)在用數(shù)學(xué)語言表征數(shù)學(xué)概念、數(shù)學(xué)性質(zhì)與數(shù)學(xué)定理等，而“形”是實(shí)物、圖象與圖形的表征。勾股定理是中國傳統(tǒng)數(shù)學(xué)文化代表之一，在教學(xué)中，為了讓學(xué)生更深層次地領(lǐng)悟知識、感悟數(shù)形結(jié)合的思想，教師可以借助數(shù)學(xué)文化把數(shù)形結(jié)合思想融入各個教學(xué)環(huán)節(jié)中。

一、基于滲透數(shù)形結(jié)合思想的“勾股定理”教學(xué)設(shè)計(jì)

（一）教材分析

“勾股定理”是人教版數(shù)學(xué)教材八年級下冊的內(nèi)容，學(xué)生已經(jīng)初步掌握開方、解方程、三角形等相關(guān)知識。教師可以結(jié)合八年級學(xué)生具有較強(qiáng)的好奇心和求知欲的特點(diǎn)，在教學(xué)中分層、分階段地滲透數(shù)形結(jié)合的思想。基于此，教師可以借助數(shù)學(xué)文化載體，對定理的由來、探索證明方法、應(yīng)用過程中滲透數(shù)形結(jié)合思想進(jìn)行設(shè)計(jì)，為學(xué)生后續(xù)學(xué)習(xí)平面幾何乃至立體幾何做好鋪墊[1]。

（二）教學(xué)目標(biāo)

（1）讓學(xué)生主動探索“發(fā)現(xiàn)”勾股定理的證明過程，并會用面積法證明勾股定理。

（2）在探索與證明勾股定理的過程中滲透數(shù)形結(jié)合的思想方法，培養(yǎng)學(xué)生發(fā)現(xiàn)問題和總結(jié)規(guī)律的能力。

（3）在學(xué)生動手操作過程中，培養(yǎng)學(xué)生的合作學(xué)習(xí)的能力，使學(xué)生體會到勾股定理中“數(shù)”與“形”的關(guān)系，感受到數(shù)學(xué)中的美。

（三）教學(xué)重點(diǎn)、難點(diǎn)

教學(xué)重點(diǎn)：探索勾股定理的推導(dǎo)過程。

教學(xué)難點(diǎn)：運(yùn)用數(shù)形結(jié)合的思想證明勾股定理。

（四）教學(xué)過程

【第一環(huán)節(jié)】實(shí)踐操作，提出猜想，導(dǎo)入課題

1.小組合作，感知數(shù)與形之間的奧秘

教師課前準(zhǔn)備好三張直角三角形紙片（三邊長是勾股數(shù)），通過PPT展示以下任務(wù)。

（1）用直尺量出直角三角形三邊長度，將數(shù)據(jù)填入表1。

（2）思考：你發(fā)現(xiàn)了什么規(guī)律？

預(yù)設(shè)：學(xué)生發(fā)現(xiàn)規(guī)律較困難時，教師提醒兩直角邊長的平方和與斜邊長的平方的關(guān)系。

設(shè)計(jì)意圖：設(shè)計(jì)思路改變了傳統(tǒng)的教學(xué)模式，直接讓學(xué)生主動建構(gòu)，從“直角三角形紙片”到“測量各邊長度”的過程中，直觀地感知數(shù)與形之間的關(guān)系。

2.運(yùn)用現(xiàn)代信息技術(shù)，體驗(yàn)數(shù)與形的動態(tài)關(guān)系

教師操作幾何畫板，設(shè)計(jì)大小不一的直角三角形;測量三邊長度（軟件操作）。

學(xué)生通過觀察進(jìn)一步激發(fā)探索和發(fā)現(xiàn)的欲望。

設(shè)計(jì)意圖：運(yùn)用幾何畫板動態(tài)地展示各種直角三角形，讓學(xué)生觀察直角三角形三邊長的關(guān)系，潛移默化地將數(shù)形結(jié)合思想滲透在動靜之中。

3.提出猜想，導(dǎo)入課題

教師引導(dǎo)學(xué)生大膽提出猜想結(jié)論：如果直角三角形的兩條直角邊長為a、b，斜邊長為c，則a2+b2=c2。由此導(dǎo)出課題——勾股定理。

【第二環(huán)節(jié)】探索新知，驗(yàn)證定理，證明結(jié)論

1.借助數(shù)學(xué)文化，再現(xiàn)發(fā)現(xiàn)定理的過程

教師出示PPT展示任務(wù)：（1）讓學(xué)生拿出課前準(zhǔn)備的四個全等的三角形教具;（2）讓學(xué)生分組進(jìn)行拼圖，并鼓勵他們大膽嘗試各種拼法。

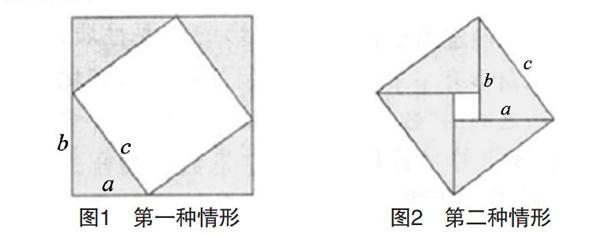
預(yù)設(shè)1：拼成第一種情形（見圖1）或第二種情形（見圖2）。

教師屏幕展示圖1和圖2，并介紹數(shù)學(xué)文化知識——趙爽弦圖。之后，教師提問：“趙爽是如何證明勾股定理的？”

學(xué)生在討論過程中總結(jié)出采用面積法得到“大正方形面積=四個全等直角三角形的面積+小正方形的面積”，從而得出結(jié)論：a2+b2=c2.

教師出示PPT展示畢達(dá)哥拉斯證明勾股定理的圖形，讓學(xué)生自己嘗試證明的過程。

設(shè)計(jì)意圖：讓學(xué)生經(jīng)歷動手操作到“再創(chuàng)造”的過程，感受中外數(shù)學(xué)家運(yùn)用數(shù)形結(jié)合思想證明勾股定理的過程。

2.自主探索，總結(jié)證明定理的方法

教師通過課件展示問題：除教材中證明勾股定理的方法，還有什么方法呢？由此拓展學(xué)生的思維，引出美國第20任總統(tǒng)加菲爾德證明勾股定理時所采用的圖形是用兩個全等的直角三角形和一個等腰直角三角形拼出一個梯形。之后，教師進(jìn)一步引導(dǎo)學(xué)生思考：運(yùn)用之前學(xué)過的方法怎樣來證明勾股定理？

設(shè)計(jì)意圖：趙爽證法有創(chuàng)意、簡潔、直觀，讓學(xué)生進(jìn)行拼、湊、補(bǔ)等實(shí)踐活動，能使他們感受到我國傳統(tǒng)數(shù)學(xué)文化的精髓。此外，通過學(xué)習(xí)勾股定理的不同證法，學(xué)生能更加深刻地理解數(shù)形結(jié)合的思想內(nèi)涵。

【第三環(huán)節(jié)】鞏固新知，拓展延伸，學(xué)以致用

為了更好地幫助學(xué)生鞏固知識、提升能力，教師可以設(shè)計(jì)一系列問題與拓展練習(xí)。

1.設(shè)問反思，知識建構(gòu)

教師可以設(shè)計(jì)以下問題：（1）勾股定理具體內(nèi)容是什么？（2）在運(yùn)用勾股定理時需要注意的前提條件是什么？（3）勾股定理主要研究直角三角形的什么關(guān)系？

2.多層訓(xùn)練，夯實(shí)基礎(chǔ)

教師利用課件展示練習(xí)題：（1）將教材24頁練習(xí)改編成搶答方式，設(shè)計(jì)一些常見的勾股數(shù)，已知直角三角形的任意兩邊長，說出另一邊長。（2）因條件有限，不能直接測量池塘的兩點(diǎn)間距離，如何運(yùn)用今天所學(xué)知識解決問題？

設(shè)計(jì)意圖：為了達(dá)到鞏固新知的目的，創(chuàng)造性地設(shè)計(jì)練習(xí)（1）。練習(xí)（2）的情境設(shè)計(jì)遵循數(shù)學(xué)源于生活并服務(wù)于生活的理念，這樣做既能提高學(xué)生的學(xué)習(xí)興趣，又讓學(xué)生體會到勾股定理蘊(yùn)含的數(shù)形結(jié)合思想的應(yīng)用價值。

3.拓展延伸，滲透思想

教師提問：“能否運(yùn)用圖形解釋公式（a+b）2=a2+2ab+b2的幾何意義？”

設(shè)計(jì)意圖：勾股定理的證明體現(xiàn)了“形”轉(zhuǎn)化為“數(shù)”的過程，為防止學(xué)生出現(xiàn)思維定式，教師設(shè)計(jì)拓展性問題——解釋完全平方公式的幾何意義，讓學(xué)生體會到“數(shù)”轉(zhuǎn)化成“形”的魅力，從而理解數(shù)形結(jié)合思想的本質(zhì)。

【第四環(huán)節(jié)】歸納小結(jié)，總結(jié)思想，作業(yè)布置

1.歸納小結(jié)，總結(jié)思想

師生共同歸納總結(jié)，不僅從知識的結(jié)構(gòu)進(jìn)行梳理，還概括了本節(jié)課數(shù)形結(jié)合思想的運(yùn)用過程。學(xué)生在總結(jié)反思過程中感受到數(shù)形結(jié)合思想貫穿于本節(jié)課的始終。

2.作業(yè)布置，運(yùn)用思想

（1）如圖3所示，一根長為10米的竹竿AB，竹竿的頂端A距離垂直地面長為8米，如果頂端A點(diǎn)下滑2米后，變成CD位置，竹竿的底端是否也滑動了2米？

（2）借助網(wǎng)絡(luò)收集新的證明勾股定理的方法。

二、對教學(xué)設(shè)計(jì)做進(jìn)一步思考

（一）在教學(xué)過程中有效利用現(xiàn)代信息技術(shù)滲透數(shù)形結(jié)合思想

以“勾股定理”的教學(xué)設(shè)計(jì)為例，教師可以通過運(yùn)用現(xiàn)代信息技術(shù)（幾何畫板），在教學(xué)中呈現(xiàn)出不同類型的直角三角形，讓學(xué)生在多變的圖形中感受數(shù)量的變化，進(jìn)一步發(fā)現(xiàn)不變的數(shù)量之間存在的規(guī)律。在教學(xué)設(shè)計(jì)中，教師從傳統(tǒng)數(shù)學(xué)文化的角度展現(xiàn)古今中外數(shù)學(xué)家運(yùn)用數(shù)形結(jié)合思想證明勾股定理的方法，使學(xué)生通過再探索、再創(chuàng)造去學(xué)習(xí)和理解了勾股定理。

（二）在問題解決過程中展現(xiàn)數(shù)形結(jié)合思想

教師應(yīng)在解決數(shù)學(xué)問題過程中，展現(xiàn)數(shù)形結(jié)合思想的關(guān)鍵——呈現(xiàn)問題中的“數(shù)”與“形”互為一體，把復(fù)雜的問題簡單化。“勾股定理”的教學(xué)設(shè)計(jì)從導(dǎo)入、定理證明及其應(yīng)用，設(shè)計(jì)了有層次、有梯度的數(shù)學(xué)問題，如從學(xué)生動手測量、觀察到動手操作拼圖，逐步滲透數(shù)形結(jié)合的思想。

（三）在教學(xué)反思過程中總結(jié)數(shù)形結(jié)合思想方法

關(guān)于反思的認(rèn)識，弗賴登塔爾認(rèn)為是建構(gòu)到反思，反思到證明的過程。教師的教學(xué)反思主要體現(xiàn)在四個方面：一是挖掘教材中蘊(yùn)含的數(shù)形結(jié)合思想;二是在教學(xué)活動的各環(huán)節(jié)滲透數(shù)形結(jié)合思想;三是數(shù)形結(jié)合思想的滲透過程伴隨知識的生長過程;四是分析例題設(shè)計(jì)習(xí)題練習(xí)，讓學(xué)生時刻受到這種方法的熏陶，從而逐步形成數(shù)形結(jié)合的意識。比如，在“勾股定理”的教學(xué)設(shè)計(jì)中，從“形”的角度看，四個全等三角形的拼湊方法主要采用了活動探究式教學(xué)方法;從“數(shù)”的角度看，勾股定理結(jié)論的呈現(xiàn)就是數(shù)形結(jié)合的思想。在教學(xué)的各個環(huán)節(jié)，教師應(yīng)始終遵循反思滲透的原則，以便有效地滲透數(shù)形結(jié)合思想。

綜上所述，在“勾股定理”的教學(xué)過程中滲透數(shù)形結(jié)合思想方法，教師應(yīng)遵循學(xué)生的思維發(fā)展特點(diǎn)，運(yùn)用現(xiàn)代信息技術(shù)動態(tài)地展現(xiàn)“形”，在解決問題的過程中靈活運(yùn)用“數(shù)”與“形”的關(guān)系，反思數(shù)形結(jié)合思想的內(nèi)在價值，從而提升學(xué)生解決數(shù)學(xué)問題的能力，提高學(xué)生的綜合素質(zhì)。

【參考文獻(xiàn)】

孫悅，劉金魁.新課標(biāo)下初中數(shù)學(xué)教學(xué)案例設(shè)計(jì)：以“探索勾股定理”為例[J].凱里學(xué)院學(xué)報(bào)，2020（12）：109-111.