基于切線不等式背景下的一類數(shù)列放縮問(wèn)題
浙江省杭州市源清中學(xué) (310015) 王 凱
在人教版A版選修2-2教材第一章《導(dǎo)數(shù)及其應(yīng)用》第1.3節(jié)《導(dǎo)數(shù)在研究函數(shù)中的應(yīng)用》的配套練習(xí)B組第一題的第三小題是研究一個(gè)指數(shù)不等關(guān)系,問(wèn)題如下:
利用函數(shù)的單調(diào)性,證明不等式ex>1+x,x≠0,并通過(guò)函數(shù)圖象直觀驗(yàn)證.
通過(guò)構(gòu)造函數(shù),借助導(dǎo)數(shù)工具,這個(gè)問(wèn)題不難解決.我們可以驗(yàn)證函數(shù)f(x)=ex在(0,1)點(diǎn)的切線就是g(x)=x+1(如圖1),所以結(jié)論可以進(jìn)一步變成ex≥1+x(x∈R),我們這里把它叫做第一切線不等式.當(dāng)x>-1時(shí),不等式兩邊同時(shí)取自然對(duì)數(shù)可得x≥ln(1+x),此時(shí)將不等式中的x用x-1替換掉后可得一個(gè)關(guān)于自然對(duì)數(shù)的不等關(guān)系lnx≤x-1(x>0),我們同樣可以驗(yàn)證函數(shù)f(x)=lnx在(1,0)點(diǎn)的切線就是g(x)=x-1(如圖2),我們這里稱其為第二切線不等式.以下我們就基于這兩個(gè)切線不等式來(lái)解決一類數(shù)列的放縮問(wèn)題.
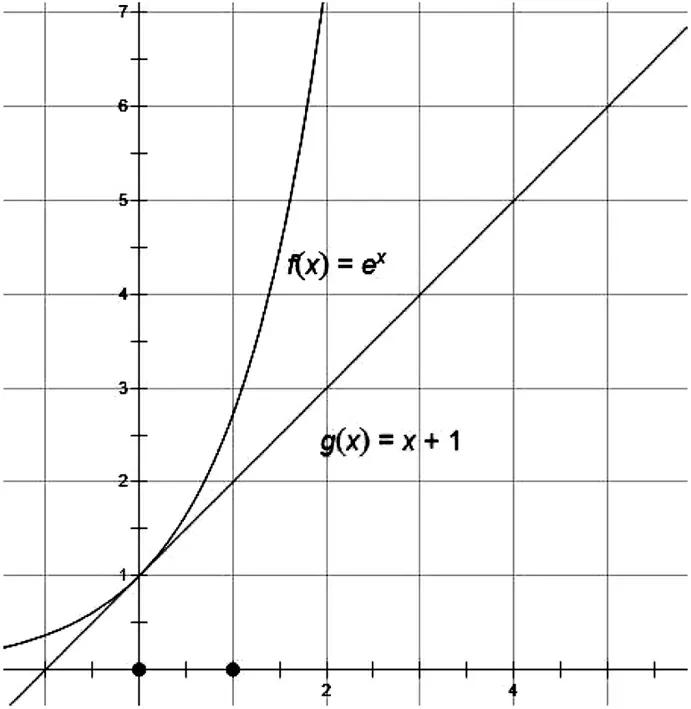
圖1
例1 已知數(shù)列{an}中,a1,a2,a3,a4成等差數(shù)列,且3a1-a2+a3+1=ea2+a3-a4.若a2<0,則( ).
A.|a1|>|a2|且|a3|>|a4|
B.|a1|>|a2|且|a3|<|a4|
C.|a1|<|a2|且|a3|>|a4|
D.|a1|<|a2|且|a3|<|a4|
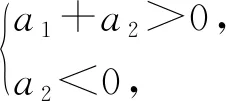
如果我們不用第一切線不等式,也可以通過(guò)構(gòu)造函數(shù),用導(dǎo)數(shù)來(lái)探究目標(biāo)函數(shù)的單調(diào)性,進(jìn)而找到不等關(guān)系解決問(wèn)題.但這個(gè)過(guò)程就會(huì)比較繁雜臃腫,小題大做也會(huì)降低解題的效率.下面我們來(lái)看2018年浙江省高考卷選擇題的壓軸題.
例2 已知a1,a2,a3,a4成等比數(shù)列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,則( ).
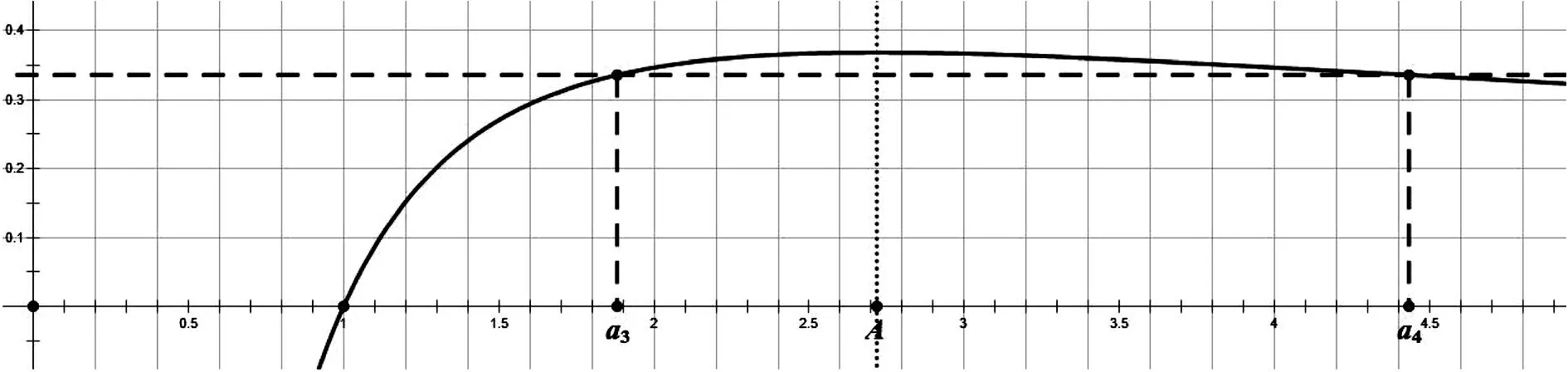
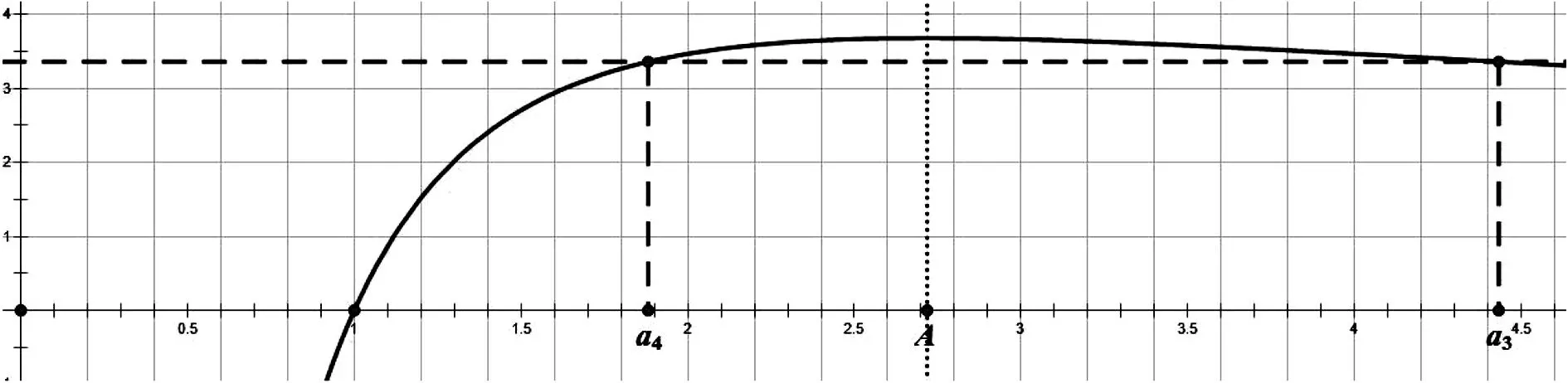
A.a1 C.a1 解析:由第二切線不等式可得a1+a2+a3+a4=ln(a1+a2+a3)≤a1+a2+a3-1,所以a4≤-1,即a1q3≤-1,可得q<0.選項(xiàng)要我們判斷a1、a3和a2、a4的大小關(guān)系,即考察這個(gè)等比數(shù)列奇數(shù)項(xiàng)和偶數(shù)項(xiàng)的單調(diào)性,本質(zhì)上就是判斷判斷q和-1的大小關(guān)系.若當(dāng)q<-1時(shí),a1+a2+a3+a4=a1(1+q)+a1q2(1+q)<0,而a1+a2+a3=a1(1+q+q2)=a1[1+q(1+q)]>a1>1,即ln(a1+a2+a3)>0,此時(shí)a1+a2+a3+a4≠ln(a1+a2+a3),所以這種情況不成立,故q∈(-1,0),那么有a1-a3=a1(1-q2)>0,即a1>a3,同理a2>a4.所以答案為B. 這個(gè)問(wèn)題借助第二切線不等式去掉對(duì)數(shù)符號(hào)后,通過(guò)選項(xiàng)的提示讓我們明確了問(wèn)題解決的方向.這樣一道高考選擇壓軸題能被我們輕而易舉的拿下,下面我們?cè)賮?lái)看一個(gè)例子. 例3 (浙江省紹興市上虞區(qū)2019年高三二模)已知數(shù)列{an}是公比為q(q≠±1)的等比數(shù)列,且a1>0,則下列敘述中錯(cuò)誤的是( ). A.若a2+a4=lna1+lna3,則q<1. B.若a2+a3=ea1+ea4,則q<-1. C.若a1ea2=a3ea4,則(a2+1)(q+1)<0. D.若a1lna4=a2lna3,則(a3-e)(q-1)>0. 先不妨假設(shè)a3 圖3 若a3>a4(如圖4),那么有a3>e得到a3-e>0.此時(shí)又有a3>a4得到q<1,所以q-1<0.結(jié)論同樣為(a3-e)(q-1)<0.故D選項(xiàng)的說(shuō)法不成立. 圖4 這類問(wèn)題的一個(gè)基本特質(zhì)是含有自然指數(shù)和對(duì)數(shù)的結(jié)構(gòu),最終的目的是要確定一種不等關(guān)系.此時(shí)我們可以嘗試一下這類源于課本的切線不等式,我們只需要一步簡(jiǎn)單的放縮,接下通過(guò)代數(shù)運(yùn)算可以幫我們快速的解決這類數(shù)列中的不等關(guān)系,所以在高三的復(fù)習(xí)教學(xué)中要給予足夠的重視.
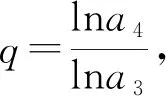
——浙江省中西醫(yī)結(jié)合醫(yī)院結(jié)核科
——張脆音

