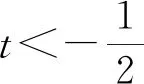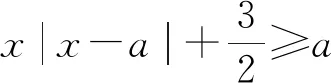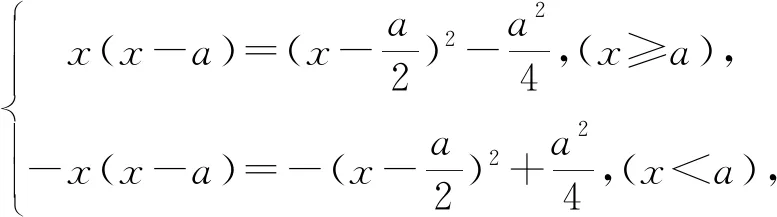例析絕對(duì)值不等式問(wèn)題的四種求解策略
江蘇省南京市漂水區(qū)第三高級(jí)中學(xué) (211200) 趙 婷
含有絕對(duì)值的不等式問(wèn)題的求解策略總的來(lái)說(shuō)有兩種:即化掉絕對(duì)值符號(hào)和利用絕對(duì)值的性質(zhì)變形化簡(jiǎn),而對(duì)于各種典型的題目來(lái)說(shuō),根據(jù)不同的特點(diǎn)又有如下四種簡(jiǎn)求策略,下面通過(guò)典型例題的分析簡(jiǎn)述這些方法,希望對(duì)讀者朋友有所幫助.
一、利用絕對(duì)值的性質(zhì)
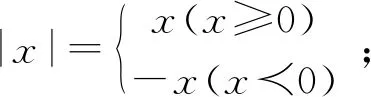
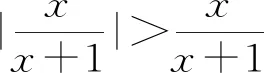
A. {x|x≠-1} B. {x|x>-1}
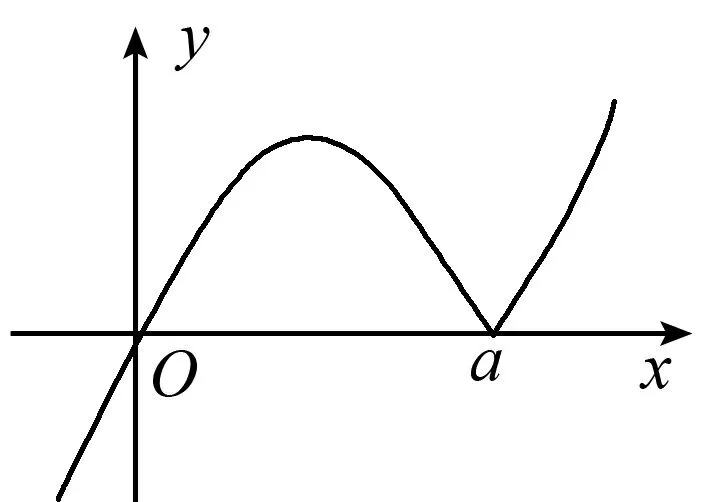
C. {x|x<0且x≠-1} D. {x|-1 評(píng)注:根據(jù)絕對(duì)值不等式的性質(zhì)直接解不等式,抓住了問(wèn)題的實(shí)質(zhì),活用絕對(duì)值的性質(zhì)解題,輕松自如. 例2 若存在x<0,使不等式x2<2-|x-t|成立,求實(shí)數(shù)t的取值范圍. 評(píng)注:通過(guò)反解不等式,使待求的參數(shù)t分離出來(lái),然后構(gòu)造函數(shù),利用不等式的值域解決了不等式有解問(wèn)題,這是求解不等式中參數(shù)范圍的常用方法,而用解不等式的方法化解絕對(duì)值問(wèn)題是解此類題的特色. 例3 求不等式|x-2|-|2x+1|>1的解集. 解析:原不等式為|x-2|>1+|2x+1|,由于此不等式兩邊都是非負(fù)數(shù),將其兩邊平方得x2-4x+4>1+2|2x+1|+4x2+4x+1,即2|2x+1|<2-8x-3x2,故3x2+8x-24x+2<2-8x-3x2,解得-2 評(píng)注:如果能確定不等式的兩邊都是非負(fù)數(shù),可直接進(jìn)行兩邊平方運(yùn)算,如果一邊是非負(fù)數(shù),另一邊不確定也可以通過(guò)分類討論后,再對(duì)適合的部分進(jìn)行兩邊平方運(yùn)用,從而達(dá)到解題目的. 例4 已知a>0且a≠1,若0 |loga(1-x)|>|loga(1+x)|. 評(píng)注:此題的解法比較多,可以分別從去掉絕對(duì)值符導(dǎo)、對(duì)底數(shù)a分類處理等方面考慮,但采用兩邊同時(shí)平方的方法可以同時(shí)解決這兩個(gè)問(wèn)題,所以是一個(gè)比較優(yōu)化的方法. 對(duì)于|x-a|±|x-b|類型的題目即可,由數(shù)軸上點(diǎn)x的位置來(lái)討論得出值域;也可用分類討論化為分段函數(shù),通過(guò)畫(huà)圖象可知其值域.而其它形式絕對(duì)值范圍問(wèn)題也可以轉(zhuǎn)化為特殊函數(shù),再利用函數(shù)圖像分析求解. 例5 已知a>0,不等式|x-4|+|x-3| 解析:設(shè)實(shí)數(shù)x,3,4在數(shù)軸上對(duì)應(yīng)點(diǎn)分別為P,A,B,則有函數(shù)y=|x-4|+|x-3| =|PA|+|PB|,當(dāng)P在A、B之間時(shí)有|PA|+|PB|=1,當(dāng)P在A、B之外時(shí),有|PA|+|PB|>1,故有y≥1,故按題意只須a>1,即a的范圍是(1,+∞). 評(píng)注:抓住題目中兩個(gè)絕對(duì)值中自變量x的系數(shù)相同這一特點(diǎn),可以得到的一個(gè)簡(jiǎn)單解法,如果系數(shù)不同,就只能通過(guò)分類討論將函數(shù)式中的絕對(duì)值化去,再利用分段函數(shù)的圖像分析幫助解決最值問(wèn)題. 圖1 圖2 評(píng)注:經(jīng)過(guò)對(duì)題目整體考察,研究其函數(shù)的特點(diǎn),即過(guò)原點(diǎn)、是奇函數(shù)等,再利用其函數(shù)圖象,建立不等式組解決了參數(shù)a范圍問(wèn)題.如果試圖通過(guò)直接解這個(gè)含有絕對(duì)值的不等式是相當(dāng)困難的. 絕對(duì)值不等式解題的一個(gè)重要思路就是化去絕對(duì)值符號(hào),將其轉(zhuǎn)變?yōu)槠胀ǖ牟坏仁剑侄斡懻撌腔ソ^對(duì)值符號(hào)的最常用的手段. 例7 解關(guān)于x的不等式|loga(ax2)|<|logax|+2,其中a>1. 評(píng)注:分段討論是解決多個(gè)絕對(duì)值和一些比較復(fù)雜的絕對(duì)值不等式的基本方法,這里要注意分段點(diǎn)的確定和最后解題結(jié)論的整體表述. 圖3 解析:設(shè)f(x)=x|x-a|,要使不等式恒成立,即使 評(píng)注:本題是不等式恒成立問(wèn)題,通過(guò)分析知道問(wèn)題的核心是絕對(duì)值函數(shù)的最小值問(wèn)題,由于函數(shù)式中有參數(shù),分類討論是化解本題難點(diǎn)的重要途徑. 絕對(duì)值不等式問(wèn)題是不等式與絕對(duì)值交匯的問(wèn)題,這是高中階段常見(jiàn)的題型,一般都是考慮先解決絕對(duì)值的問(wèn)題,然后轉(zhuǎn)化為普通不等式或不等式組的問(wèn)題,由于題目的條件與結(jié)論不同,可能出現(xiàn)多種情況,但總體的解題方針和解題方向是一致的.
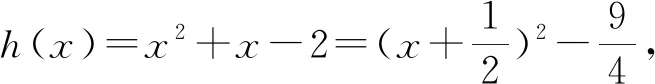
二、兩邊同時(shí)平方
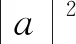
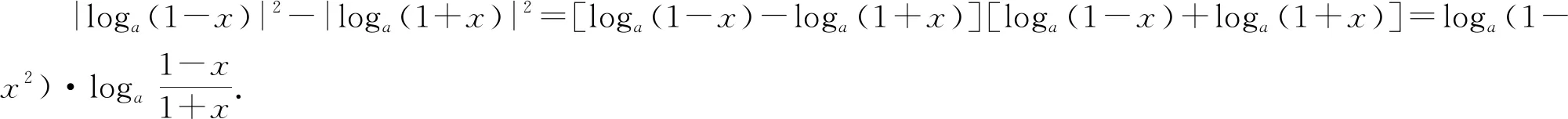
三、以形助數(shù)
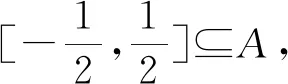
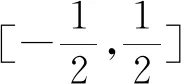
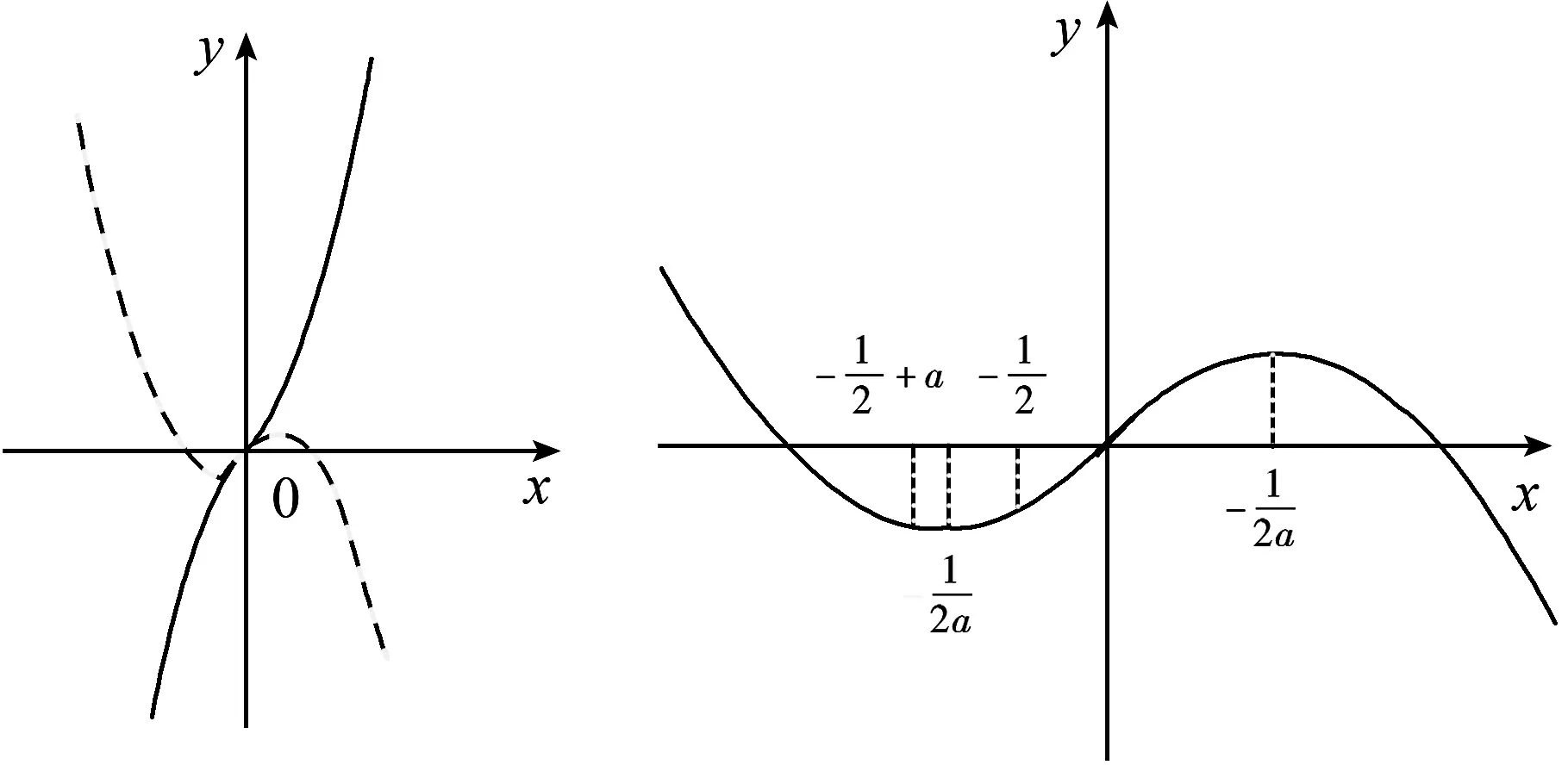
四、分類討論