基于核心素養評價框架的試題命制研究*
——以函數綜合題的命制為例
福建省莆田第十中學 (351100) 黃啟賢
基于數學學科核心素養的命題應具備以下環節:構建學科核心素養的評價框架;依據評價框架編制基于核心素養的試題;給出評分標準及相應的核心素養的水平劃分依據[1].
1 構建評價框架
以高考命題的要求:“基礎性、綜合性、應用性、創新性[2]”為標準,以數學核心素養的水平劃分為基礎,將知識學習的過程劃分為三個階段,構建如表1所示的核心素養評價框架.
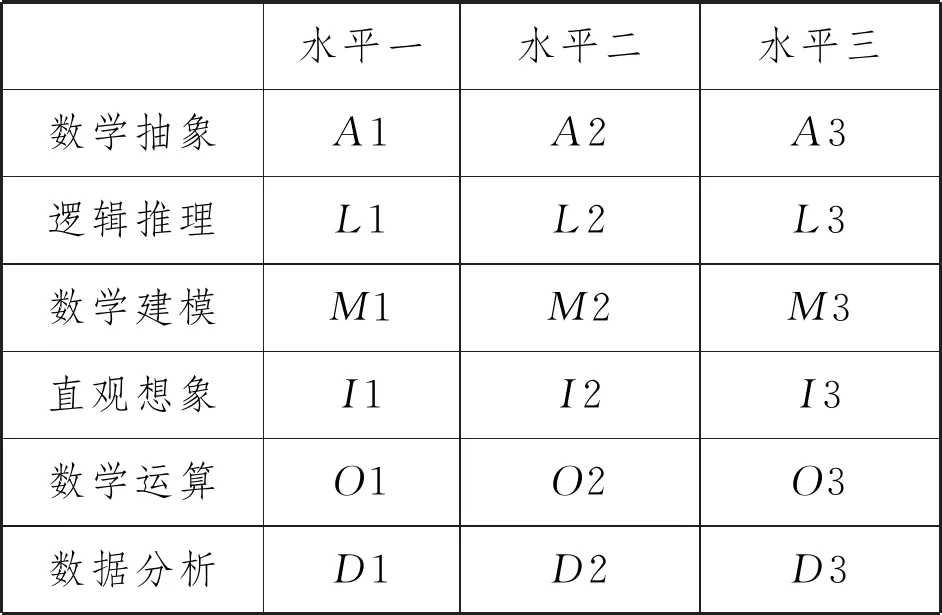
表1 核心素養評價框架
核心素養水平一是高中畢業應達到的要求,也是知識學習過程中的知識理解階段.主要是指在熟悉的情境中,選擇合適的定理、性質等解決一些簡單的相似的問題,感悟過程中的通性通法,形成良好的思維品質,會用數學直觀來有條理地解釋實際情景中與數學相關的問題.
核心素養水平二是高考應達到的要求,也是知識學習過程中的知識遷移階段.主要是指在關聯的情境中,選用合適的定理、性質,設計合理運算程序,構建恰當的數學模型等解決一些較為復雜的問題,感悟概念、命題、定理之間的內在邏輯,理解數學思想方法,形成規范化思考問題的品質,會用模型的思想闡釋生活中的隨機現象.
核心素養水平三是針對部分必修或選擇性必修的內容提出的要求,也是知識學習過程中的知識創新階段.主要是指在綜合的情境中,發現數學研究對象,能在結論的基礎上形成新的命題,能對復雜問題,構建過渡性命題,建立恰當的數學模型來解決問題.感悟數學原理,會用數學原理闡釋生活現象.
2 編制基于核心素養的試題
試題能夠啟發學生在日常生活中發現數學,學習數學,引導學生主動思考,進而提高學習興趣和解決實際問題的能力[4].基于核心素養的試題命制,圍繞數學內容主線,關注知識、方法、素養的落實與比重分布,合理設置試題普適性與區分度.文章以一道函數綜合題的命制過程為例,展示基于數學學科核心素養的試題命制過程.
2.1 意圖分析
《中國高考評價體系》通過“一核”“四層”“四翼”6個字高度概括了試題命制的目的、內容及要求,提出了命題理念從“知識立意”“能力立意”向“價值引領、素養導向、能力為重、知識為基”的轉變[2].高考的評價體系下的函數綜合題的命制應遵循以下幾個方面.從考查目的看,問題的設計應允許多角度作答,引導學生從“解題”到“解決問題”的轉變.從考查內容看,試題以指、對、冪函數與三角函數的組合運算為載體,檢測函數的圖象與性質的深入理解與綜合應用等必備知識,要求學生靈活應用各種數學思想方法來解題,同時也考查學生的數學學科素養.從考查要求看,函數綜合題置于壓軸題的位置,體現試卷的效度與區分度,強調知識的應用與創新,其中分值安排為:基礎性約占30%,綜合性約占30%,應用性與創新性約占40%.
2.2 素材選取
函數綜合題多由指數型函數、對數型函數、冪函數型函數、三角函數的運算或復合得到的,考查函數的單調區間、最值、極值、零點等性質及其應用.由于三角函數所特有的有界性與周期性,使得三角函數與其他函數相結合為載體的試題中,在考察性質或應用時,需用到放縮比較、估值分析、周期討論等,有較強的綜合性和創新性.擬選用三角函數與對數型函數組合的形式作為試題載體,取2019年全國理數I卷20題以函數f(x)=sinx-ln(1+x)為素材.
2.3 試題初擬
在2019年試題中,所選用的函數是三角函數與對數型函數組合的形式,故試題有以下改編設想.將sinx改變為asinx+bcosx,或axsinx,或axcosx,將ln(1+x)改變為aln(b+x),或aex+b,或ax2+bx+c,或幾個的組合.第一問設定為求單調區間或值域等相關問題.第二問設定為判斷或求極值點、或零點相關的問題.在問題的設計上,考慮到學生思維的整體性、連貫性、遞進性,在難度與知識的關聯度上逐層推進、逐步提高.在第二問中要求學生構建過渡性命題,構造運算程序,抓住問題的本質,以解決問題,體現命題的選拔功能.
首先,嘗試將sinx改為acosx,即f(x)=acosx-ln(1+x).當a<0時,f(x)的圖象如圖1所示(取a=-2),當a>0時,f(x)的圖象如圖2所示(取a=2).初步探究其知識點、蘊含的學科素養等,可知基本上與原題重疊,解題思維、解題方法與原題基本一致,故不予選用.
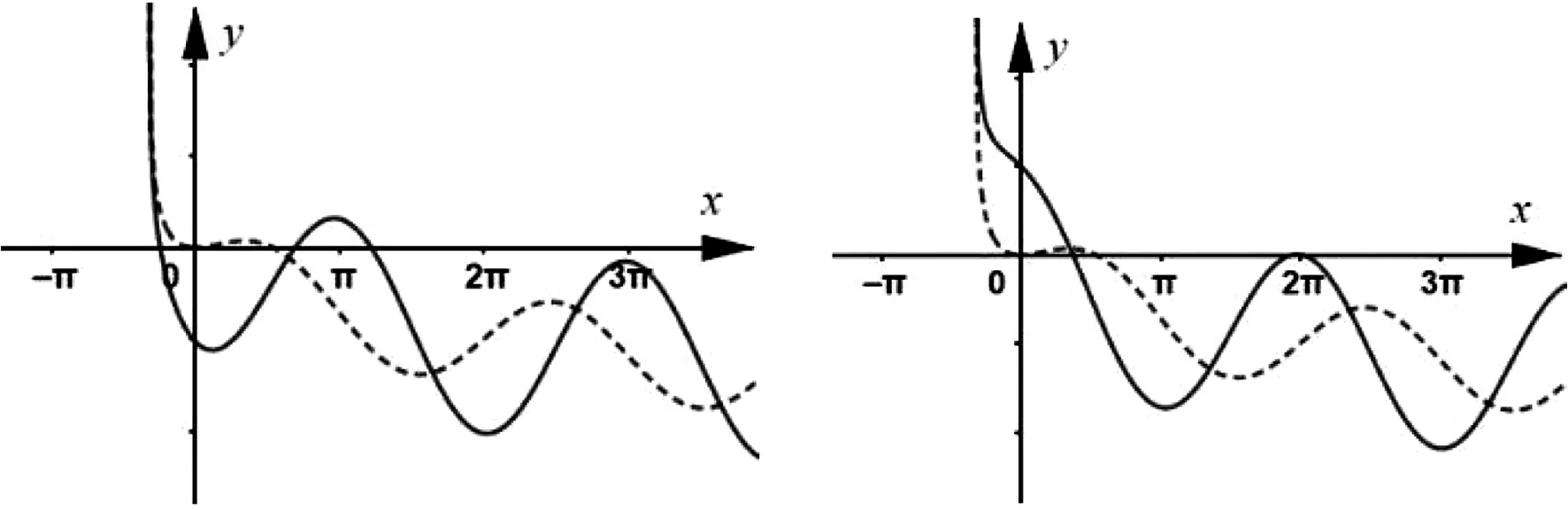
圖1 圖2
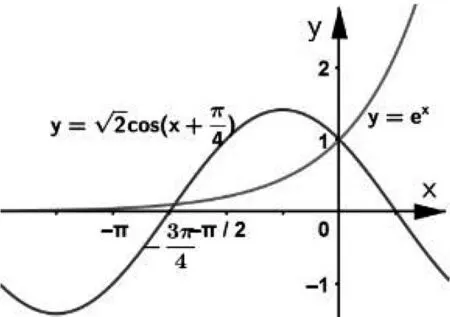
進一步設想,將f(x)=sinx-ln(1+x)中的ln(1+x)改為aex,即f(x)=sinx-aex.當a=1時其圖象如圖3所示.此時可設計第一問:當x≥0時,f(x)≤-1.嘗試證明驗證:f′(x)=cosx-ex,∵當x≥0時,cosx≤1,ex≥1,∴當x≥0時,f′(x)=cosx-ex≤0,∴f(x)在[0,+∞)上遞減,∴f(x)≤f(0)=-1.如圖4,觀察y=sinx與y=ex的圖象的關聯度以及從設問的驗證過程,可以看出雖然題目的切入點低,但條件的約束性可進一步加強.
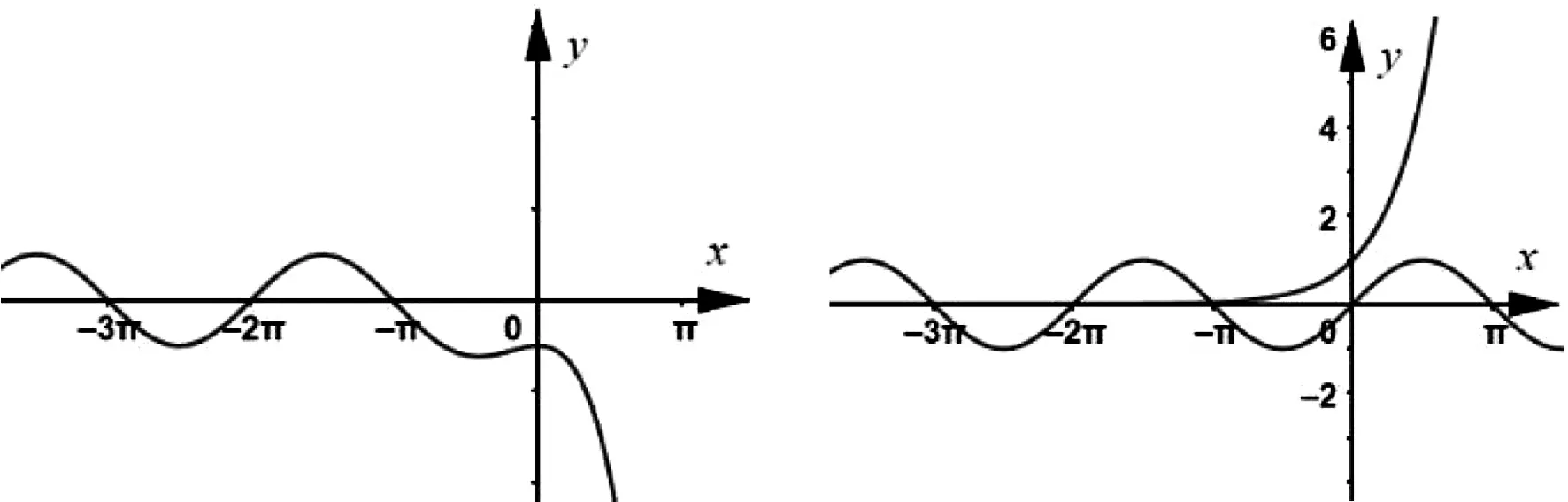
圖3 圖4
考慮到y=xex過原點,嘗試將ex替換為xex.觀測圖5中的y=sinx與y=xex的圖象,以及圖6中函數f(x)=sinx-xex的圖象特征,初步能達到預期目標.

圖5 圖6
當x≥0時,y=sinx與y=xex兩圖象恰有公共點為O(0,0),且當x∈[0,+∞)時,y=xex的圖象始終在y=sinx的上方.當x∈(-∞,0)時,y=xex的圖象在x軸的下方.觀察圖象可知,y=sinx與y=xex的交點落在((2k-1)π,2kπ),k∈Z且k≤0上,且每個區間有2個零點.依據命題預設,初擬試題如下:已知函數f(x)=sinx-xex,證明:(1)當x≥0時,f(x)≤0;(2)當-π 對初擬試題第(1)問的嘗試證明可知,題干中的函數改為f(x)=sinx-xex之后,試題的切入點沒有顯著提升,但考查的角度、考查的知識點更豐富,蘊含的思想方法更多樣性,其中包含了導數運算法則的使用、三角函數的有界性、(x+1)ex≥ex≥1的放縮運算、單調區間的判斷、根據單調性求值域等. (1)解法1:∵當x≥0時,cosx≤1,(x+1)ex≥ex≥1,∴當x≥0時,f′(x)=cosx-(x+1)ex≤0,∴f(x)在[0,+∞)上遞減,∴f(x)≤f(0)=0.命題得證. 解法2:∵當x≥0時,ex≥1,∴-xex≤-x,∴sinx-xex≤sinx-x.設g(x)=sinx-x(x≥0),g′(x)=cosx-1≤0,∴g(x)在[0,+∞)上遞減, ∴g(x)=sinx-x≤g(0)=0,∴當x≥0時,f(x)=sinx-xex≤0.命題得證. (2)解法1:f′(x)=cosx-(x+1)ex,f″(x)=-sinx-(x+2)ex. 綜上,當-π 圖7 以下從試題參數的引入、知識的交匯、以及命題的等價轉換等方面可對試題作拓展研究. 拓展1(引入參數探究)已知函數f(x)=sinx-axex,(1)若a=1,證明:當x≥0時,f(x)≤0;(2)當-π 拓展2(與數列交匯命題)已知函數f(x)=sinx-xex,證明:(1)當x≥0時,f(x)≤0;(2)f(x)在(-∞,0)上的零點從大到小排列為:a1,a2,…,an,…,求使得|a1|+|a2|+…+|ak|<100π成立的k的最大值. 該題是函數綜合題,是數學試卷中的壓軸題,屬于知識綜合運用的題目,借助數學軟件GeoGebra實驗探究,將指數型函數與三角函數巧妙結合考查函數恒成立及零點問題.在數學對象的數學運算過程中考查學生新數學情景下知識遷移、知識創新能力.兩步的分值分別設定為5分、7分. 第(1)問是探究函數的最值問題.解法一是借助求導法判斷函數的單調性,再其利用比較大小,其間用到了放縮(x+1)ex≥ex≥1、引入中間值等.解法二是用分析法,先以放縮法得到sinx-xex≤sinx-x,再結合單調性的應用得最值,屬于知識遷移層面.體現了學科的基礎性與綜合性,其涉及的核心素養水平劃分為L2、I2、O2. 從邏輯推理素養方面看,涉及到函數y=ex,y=xex,y=sinx的圖象與性質的理解,并利用其性質進行論證.如果論證途徑清晰,推理過程表述嚴謹,根據加分原則,可以認為達到L2的要求,得2分.從直觀想象素養方面看,導數與單調性的轉化,單調性的圖形表示,要求學生明確代數與幾何的關聯,并依此解決問題.如果函數與圖形轉換合理,問題得以解決,根據加分原則,可以認為達到I2的要求,得1分.從數學運算素養方面看,涉及到導數的運算,三角函數的有界性,(x+1)ex≥ex≥1的放縮運算,單調區間的判斷,根據單調性求值域等.此處若運算過程合理,結論正確,根據加分原則,認為達到O2的要求,得2分. 第(2)問是探究函數零點的存在性問題,學生在經歷第(1)問的基礎上,對函數有了從數到形,從抽象到直觀的認識,屬于知識創新層面.體現了知識的綜合性與創新性.其涉及的核心素養水平劃分為A3、L3、I3、O2. 從數學抽象素養方面看,由于三角函數與y=(x+n)ex,n∈N+的單調區間不同,需要分類討論.若能分類合理,討論嚴謹當,抽象合理,根據加分原則,可以認為達到A3的要求,得2分.從邏輯推理素養方面看,要求能夠將二次導函數作為過渡性命題,再回到一節導函數,最后到原函數的探討上,進而解決問題.如果命題構建合理,推理過程嚴謹,結論符合預期,根據加分原則,可以認為達到L3的要求,得2分.從直觀想象素養方面看,要求能夠將零點問題轉化為交點問題,結合零點存在定理實現數形之間的轉換,形成解決問題的思路.如果數形轉換合理,目標達成,根據加分原則,可以認為達到I3的要求,得1分.從數學運算素養方面看,要求能夠結合三角函數的單調區間分布特點,對現有函數的區間作嘗試性分段探討,在運算過程能根據需要引入二階導數,進而解決問題,根據運算結果判斷單調性,進而求得最值,認為O2的要求,得2分.2.4 試題打磨
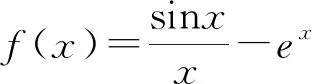
2.5 解法探究
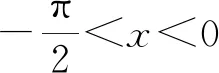
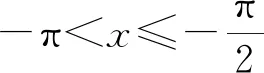
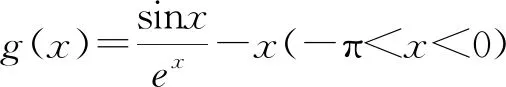
2.6 試題拓展
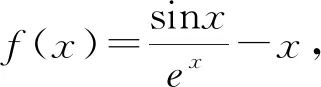
3 評分標準及核心素養的水平劃分
3.1 第(1)問的核心素養水平劃分
3.2 第(2)問的核心素養水平劃分

