數學教學中要重視數據處理能力的培養*

廣東省中山市龍山中學 (528471) 李云章

數據處理能力是現代社會發展中對學生提出的一項新要求．《普通高中數學課程標準(實驗)》對數學能力的要求有所提高,增加了數據處理能力．數據處理能力是指會收集、整理、分析數據,能從大量數據中抽取對研究問題有用的信息, 從而作出正確的判斷與決策的能力．

每一個數學問題都是由數據組成的,提高數據處理能力,能夠幫助學生找出正確的解題思路．完善的數據處理能力包含多個方面的內容,它要求學生在正確審題的基礎上能運用相關的數學方法分析數據，能利用圖象和數字等整合數據，同時能夠熟練應用計算機等輔助工具處理數據，并能夠通過計算準確得出結果等．數據處理能力不只是一般的數據統計問題，它在高中數學的很多分支上都體現出來，能夠對題目中所給的數據由識別、理解，到篩選、歸類，再到運用、發揮作用，就有可能比較完美的解決這道題．下面分類舉例介紹數據處理能力的體現和要求，供讀者朋友參考．

一、統計問題中的數據處理

統計問題在小學、初中、高中的教材都有，而高中的要求更為具體，涉及的內容也比較多，是對數據處理能力的培養的集中體現之一．

例1 某個班級的四個小組的人數分別為12、12、x、10，若已知這組數據的中位數與平均數相等且有一個眾數，試求這組數據的平均數．

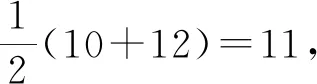
評注：本題對平均數、中位數、眾數的概念進行了考查，是較為簡單的問題，但如果對概念理解不清，數據處理能力不強，尤其是沒有分類，就會發生錯誤．

二、立體幾何問題中的數據處理

雖然說立體幾何問題是與幾何圖形相關，但有的題目中含有角的大小的計算，距離的計算和面積、體積的計算，也有的需要通過數據處理來判斷線面關系．

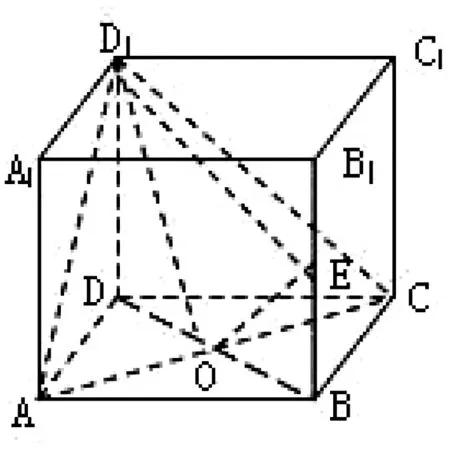
圖1

例2 如圖1，在正方體ABCD-A1B1C1D1中，E是BB1的中點，O是底面ABCD的中心.求證：OE⊥平面ACD1.

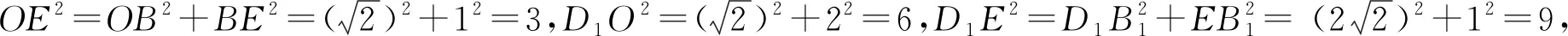
評注：正方體和正四面體等是一些特殊的幾何體，有許多的數量關系，應該利用好這一點．本題中雖然沒有給出具體數據，但通過賦值，然后再計算處理，使問題獲得解決．

三、函數問題中的數據處理

一些函數問題的題目中，會出現含有一定規律的數據出現，通過對這些數據變形和化歸處理，可以挖出當中所隱含的條件，揭示其中規律．

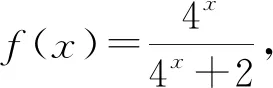
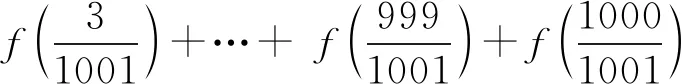
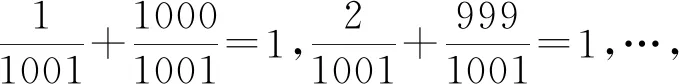
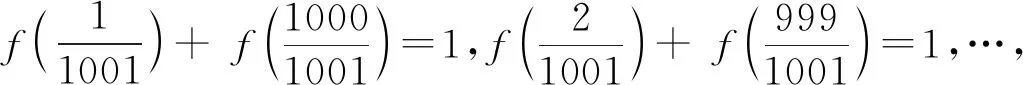
評注：有些給出的數據中隱含著等式關系，它就提示了該數學問題的本質，挖掘出這些隱含的等式關系，就是我們解答此問題的切入點．

四、解析幾何問題中的數據處理

一般的解析幾問題都是與大量的字母運算有關，但有時對一些特殊數據進行分析處理，才能抓住機會巧妙破題．

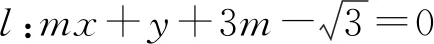
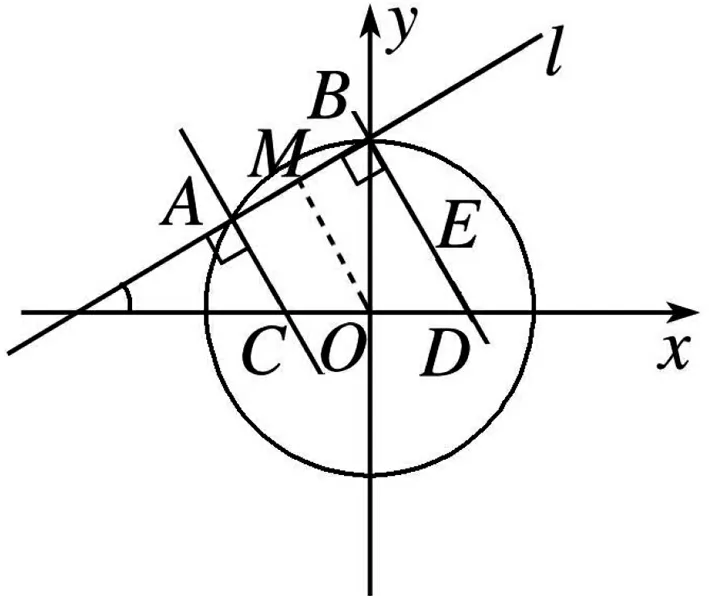
圖2

解析：如圖2，設AB的中點為M，由題意知，圓的半徑

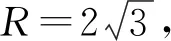
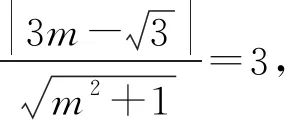
評注：在本題中抓住弦長的值分析出△OAB為等邊三角形是成功解題的重要一環，而后續解題就是圍繞如何求C,D兩點坐標進行的努力，也是比較容易達到解題目的的．

五、數列問題中的數據處理

數列中的數據比較精致，某一個數據有時都能起很大作用，如數列的下標、數列中的項和某一些表達式中的數據，我們不可輕視它的作用．

例5 在等差數列{an}中，若前n項和記為Sn，已知a3=12，S12>0，S13<0，當n為何值時，Sn最大？

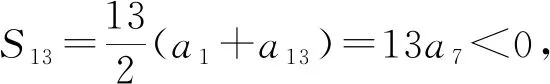
評注：本題中通過分析條件S12>0，S13<0，得出相鄰兩項a6>0，a7<0，雖然做的是數列下標的數字游戲，但問題就在這些下標變化中解決了．

六、基本不等式問題的數據處理

用基本不等式解決最值問題是高頻率的題目，其中題目條件的不同，解題方法也多種多樣，而利用數字“1”就是常用方法，必須熟練掌握．

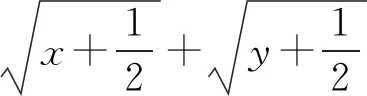
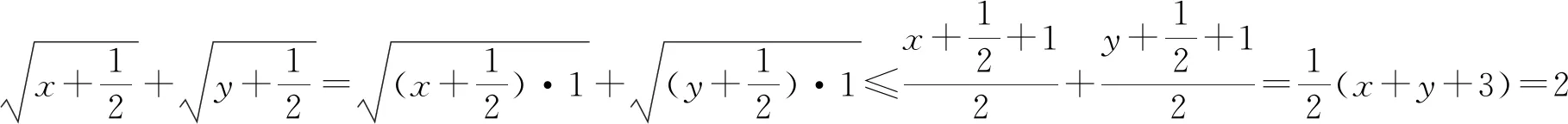
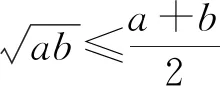
七、三角函數問題中的數據處理

三角函數中對角的數值處理比較多，要善于發現和運用某些特殊角的關系，將問題化歸分類解決．

例7 求(1+tan1°)(1+tan2°)(1+tan3°)…(1+tan44°)的值．

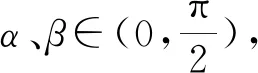
評注：通過觀察給出角的特點，尋找熟悉的三角公式的模型是分析題意的要點，靈活地將tanα+tanβ轉化為tanαtanβ的關系，這樣就為后續解題排除了障礙．

通過以上各例的分析求解我們可以知道，正確有效的數據處理有時是解決問題的關鍵，我們必須正視發展數據處理能力在高中數學中的重要性，而作為教學人員必須提醒同學們，在做題時嚴肅對待每一個數據的處理，通過足量的練習，就能使數據處理能力得到提高．