諧振接地配電網電弧接地故障暫態分析方法與辨識

楊 帆，任 偉 ，沈 煜，雷 楊 ，薛永端，徐丙垠

（1.國網湖北省電力有限公司電力科學研究院，武漢 430077；2.中國石油大學（華東）新能源學院，青島 266580；3.山東科匯電力自動化股份有限公司，淄博 255087）

受線路老化、外力破壞或暴風、暴雨等惡劣天氣影響，中壓配電網常因導線破損、墜地、絕緣子閃絡等發生單相電弧接地故障[1]。近年來，隨著配電網接地故障分析與保護算法研究的深入，經非線性電阻接地故障，尤其是電弧接地故障的建模分析、辨識、保護等已逐漸成為業內眾多專家學者研究的熱點問題[2-6]。而按照實際分析需要，在不同精度要求下對電弧接地故障合理建模并定量分析其故障特征是研究相關問題的基礎與關鍵之一。

考慮到建模分析時的復雜程度，以及實際配電網工況條件下電弧放電間隙不長、電弧電流一般偏小等因素，在中壓配電網電弧接地故障的建模分析中，傳統方法多基于描述電弧外部電氣特性的黑盒模型[7-10]。例如：文獻[7]結合電弧電流變化規律，構造一種組合的Mayr-Cassie模型，通過仿真計算分析得出電弧電壓、電流等參量的動態變化特征；文獻[8]利用仿真軟件研究Mayr、Cassie、Schwarz等模型特性，分析不同弧長對電弧阻抗、電弧接地故障暫態和穩態諧波特性的影響；文獻[9]基于中壓電纜網絡仿真驗證，對電弧黑盒模型的參數進行改進，進而得出電弧模型的電壓電流特性；文獻[10]通過仿真軟件分析控制論電弧模型參數變化對模型造成的影響等。

然而在研究配電網接地故障暫態過程及故障特征時，故障暫態電流等電氣量的定量分析嚴重依賴于故障等值電路的微分方程的求解。由于電弧黑盒模型的數學表達式同為電弧電導的微分方程形式，多適用于仿真迭代，若將其直接應用于故障等值電路，則求解方程中將出現多個微分表達式，利用現有數學工具難以求解。因此，為定量求解電弧接地故障暫態過程，現有方法多將電弧電阻簡化為線性過渡電阻后代入故障暫態等值電路，其求解結果不能體現電弧的非線性特征且誤差偏大。

針對上述問題，本文在保留電弧黑盒模型主要非線性特征的前提下，對其適當簡化，并結合故障復合等值網絡，提出一種適用于諧振接地系統電弧接地故障的暫態分析方法。首先，定量計算諧振接地配電網在不同過渡電阻下的電弧接地故障暫態電流解析表達式；然后，根據簡化模型及電弧電壓的線路衰減特性，給出一種綜合電弧電流與線路電壓諧波信息的穩定電弧接地故障辨識原理；最后，通過對比電弧動態模型仿真與人工接地實驗的結果，驗證了所提方法的有效性。

1 諧振接地系統電弧接地故障建模

1.1 非線性電弧模型的建立與簡化

基于能量守恒原理，根據不同的假定條件及參量等效方式，相關學者提出了包括Mayr模型、控制論模型、Emanuel電弧模型[11]、對數電弧模型[12]等多種電弧模型。

在Mayr電弧模型中，電弧柱表示為直徑始終不變的圓柱體通道，假設弧柱壓降與電弧電壓相等，重點考慮弧柱徑向傳導散熱，其表達式為

式中：g為電弧電導；t為時間；ih為電弧電流；τs為電弧模型時間常數；eh為弧柱中的場強；P1為單位長度電弧耗散功率；其中τs和P1均為定值。

控制論電弧模型是在Mayr電弧模型的基礎上引入電弧長度參量l，假設單位長度電弧壓降及電弧電阻為定值，且假定電弧柱中場強處處相等，其表達式為

式中：Is為金屬性接地故障穩態電流的幅值；Vs0、β′為常量系數，β′影響電弧零休時間長短，Vs0為弧隙單位厘米的壓降；l為電弧長度，cm。

Emanuel電弧模型由接地介質為沙地的高阻接地故障實驗錄波數據推導而來。圖1為Emanuel電弧模型示意，其中，VP、VN一般為幅值存在稍小差異的直流電源，可影響正負半波燃弧電壓，并與對應二極管DP、DN構成電流通路；X、R為等效電感與電阻，主要影響接地故障零序電流相量。

圖1 Emanuel電弧模型示意Fig.1 Schematic of Emanuel’s arc model

對數電弧模型可由描述低氣壓、短氣隙放電過程的湯遜原理簡化推導得到，其表達式為

式中：u為電弧電壓；UT、為常數，UT一般選取為線路電壓的10%，依據線路參量確定。

相較于中、低頻故障特征，由于實際電弧高頻特征含量偏少且極易受各類噪聲的干擾，則對于電弧接地故障辨識、保護等工程實際問題，現有算法往往選用含量多、幅值大的中、低頻帶作為相關判據的特征頻帶，工程實用效果良好。因此，為解決黑盒模型應用至等值電路后難以求解的問題，當進行電弧接地故障暫態電氣量的工程計算時，同樣可以在不影響電弧主要特征的前提下，以電弧中、低頻特征為主，合理弱化含量較少的高頻特征，從而簡化動態電弧模型，以便于后續分析。

對于多數的黑盒電弧模型，當忽略部分電弧高頻動態變化特征時，電弧電壓靜態特性一般可表示為式（3）所示的u(ih)形式，即電弧電壓可表示為電弧電流的函數。該形式無積分運算，在電路分析或仿真計算中可通過設置電流控制的受控電壓源實現。例如，控制論電弧模型靜態特性可表示為

式中，u(ih)為靜態特性的電弧電壓。

現有研究成果表明，電弧電壓諧波含量一般遠遠大于電流諧波含量，且電弧電壓諧波含量的占比隨電弧長度的變化并不明顯[8]。因此，為充分對比不同電弧模型特征，當不考慮弧長變化對電弧電壓諧波的影響時，設定適宜電弧參數[8，10]，使電弧穩定燃燒時的電壓近似相等以便于對比。對數電弧模型、控制論電弧模型、Emanuel電弧模型及控制論模型靜態表達的電弧電壓對比如圖2所示。經傅里葉變換后，主要頻次諧波對應函數式的幅值常量系數對比如表1所示。

圖2 電弧電壓波形對比Fig.2 Comparison among arc voltage waveforms

表1 電弧電壓諧波含量對比Tab.1 Comparison of arc voltage harmonic content

模型簡化會導致部分諧波信息丟失，對模型的精度產生影響。由圖2和表1對比可知，雖然各模型對電弧電壓的細節表現略有差異，但其波形形態及主要頻域特征相近，且將控制論動態電弧模型轉換為相對應的靜態模型后，電弧電壓趨似于矩形波。雖然高頻燃弧、熄弧電壓略微變小，但是穩定燃弧過程的平穩電壓波形得到有效保留，該特征與對數電弧模型、Emanuel電弧模型的表現相似（對數模型對應電弧電壓波形畸變稍小，故主要頻次諧波的幅值常量系數亦小于其他模型）。此外，由于電弧高頻特征含量較少，且平穩電壓波形中所含中低頻特征諧波分量明顯多于燃弧、熄弧過程中所含中低頻諧波分量，故其仍能反映電弧接地故障的非線性特征[13]。因此，為提高原線性過渡電阻模型在分析電弧接地故障時的準確度，本文對電弧黑盒模型進行合理簡化，采用靜態模型進行后續分析計算。

1.2 基于故障復合網絡的諧振接地系統電弧接地故障等值電路

故障等值電路通過激勵、電阻、電感及電容等元件的適當組合建立相關約束關系，可用于模擬、量化計算故障暫態主要諧振過程中的電氣量特征。文獻[14-15]分析建立的諧振接地系統接地故障暫態等值電路如圖3所示，其中，Uf為故障點虛擬電源；Lp為3倍的消弧線圈電感；C為系統所有出線對地分布電容之和；電阻R、電感L均包含故障點兩側的線模與零模信息。本文與文獻[15]不同的是R在等效過程中考慮了電弧非線性電阻。等值電路其他各參數的化簡、等效原則與計算方法亦可參照文獻[15]，此處不再贅述。

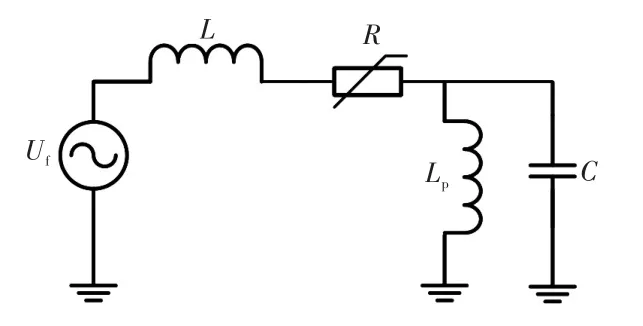
圖3 諧振接地系統電弧接地故障暫態等值電路Fig.3 Transient equivalent circuit of Peterson coil grounded system under arc grounding fault

靜態模型表現為電弧電壓與電流的函數，在電路分析或仿真計算中可通過設置電流控制的受控電壓源實現。結合電路理論與實際物理含義，將電弧電阻從總的非線性過渡電阻中分離，等效為受控電源（其在電路中仍呈阻性）與固定的線性電阻，由此可得基于受控電壓源模型的電弧接地故障等值電路如圖4所示。其中，R為固定的線性電阻，其他參數與圖3中相同。由于阻抗中流過的零序電流為3倍的單相零序電流，因此原電弧電阻亦須放大3倍，故等效后阻性的受控源電壓uarc可表示為

圖4 基于受控電壓源模型的電弧接地故障等值電路Fig.4 Equivalent circuit under arc grounding fault based on the controlled source model

在圖4所示的故障等值電路中，雖然已簡化了電弧黑盒模型的復雜積分運算，但由于等效后為受控電源形式，屬于非線性電路，仍很難直接通過現有算法定量求解非線性的故障暫態過程。因此在理論計算時，在誤差允許的范圍內，按照不同過渡電阻下的故障暫態過程分別對受控電源模型進行簡化。

由傅里葉級數可知，任何周期函數f（t）都可由正弦和余弦函數無窮級數之和表示，即

式中：a0為常數項；n為級數；an、bn分別為余弦、正弦項的系數；ω為角頻率。

而在靜態控制論模型中，由于電弧電流參量僅控制電弧電壓方向，不對電壓幅值產生影響，故在故障穩態及部分暫態過程中，電弧電壓將表現為正、負半波相等的矩形波，其幅值由弧長、弧隙單位厘米的壓降等參數決定。將靜態控制論模型的幅值h、角頻率ω的矩形波進行傅里葉級數分解可得

在故障穩態及部分暫態分析過程中，可將靜態控制論電弧模型等效為若干個不同幅值、不同奇數倍頻的電壓源串聯形式，以實現解耦，且此時各奇頻次的諧波占比顯然與表1所示分布規律相近。此外，由于不同過渡電阻下的接地故障暫態過程并不完全相同，組合的獨立交流電壓源并不能反映所有情況，當分析特定故障暫態過程時，仍需增加1個直流電壓源以滿足實際。

適用于諧振接地配電網電弧接地故障分析等值電路如圖5所示。該故障等值電路在突出電弧中頻、低頻段主要非線性特征的同時，仍保留了大部分高頻特征，大幅簡化了相關運算，并可根據需要利用疊加原理對電弧引入的不同頻次諧波進行獨立、組合分析計算，相較于傳統利用線性過渡電阻的暫態分析電路具有一定的優越性。

圖5 適用于定量分析的電弧接地故障等值電路Fig.5 Equivalent circuit under arc grounding fault for quantitative analysis

2 諧振接地系統電弧接地故障暫態分析

圖5所示的故障等值電路為三階電路，很難對故障電流進行求解，應根據實際情況將其分為高阻接地、低阻接地兩種情況進行降階處理。

2.1 高阻接地

當發生接地故障時，過渡電阻超過工頻下系統容抗的1/10稱為高阻接地，高阻接地故障一般不忽略消弧線圈的作用，又因線路的線模與零模阻抗小于過渡電阻，可以忽略不計。因此，高阻接地時故障暫態過程主要為系統電容與消弧線圈間的并聯諧振[15]，故可將圖5簡化為圖6所示的二階等值電路。

圖6 高阻接地時的電弧接地故障等值電路Fig.6 Equivalent circuit under arc grounding fault with high resistance

圖6所示的二階等值電路的微分方程特征根p1,2為

2.1.1 過阻尼

由式（9）可知，在高阻接地過阻尼條件下，原有接地故障電流表現為帶衰減直流分量的工頻電流，其在暫態過程持續時間內大多不改變方向。進而由式（4）可知，電弧電壓在暫態過程中表現為恒定的直流電壓。因此，將圖6中串聯復奇頻電壓源置0，除故障虛擬電源外僅保留直流電壓源。

當僅有直流電壓源作用時，計算可得流經故障點的電流ifDC（參考方向與if0相反）為

最后，利用疊加定理得出流經故障點的電流if為if0與ifDC之差，故障電流暫態仍為帶衰減直流分量的工頻電流形式。

2.1.2 欠阻尼

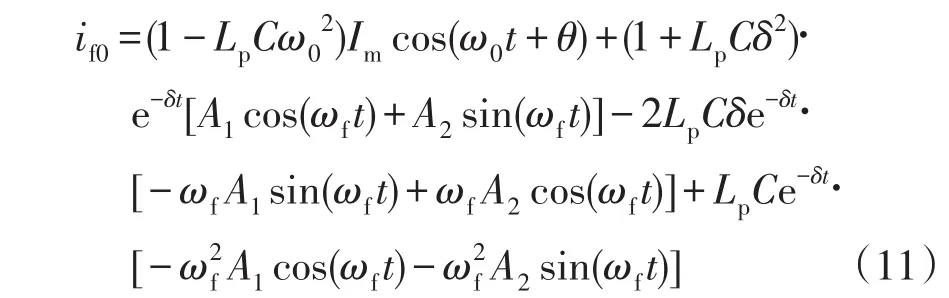
此時，故障暫態過程為以ωf為主諧振頻率的衰減振蕩過程，考慮電弧的非線性影響，則在欠阻尼暫態過程中，圖4所示模型的受控源將對外表現為周期T=2π/ωf且正、負半波相等的矩形波，其電壓方向與串聯回路電流方向相同。對該方波進行傅里葉分解，同時將直流電壓源置為0，則對于圖6所示的復奇頻電壓源串聯電弧模型，電壓源基波角頻率可近似等效為暫態主諧振角頻率，即ω=ωf。

當僅有角頻率為ω的電壓源作用時，其故障暫態電流if1表達式與式（11）類似；當僅有3次諧波（3ω）電壓源作用時，其故障暫態零模電流if3為

在高阻接地欠阻尼條件下，包含全奇頻次諧波（疊加后包含高頻段）的故障暫態零模電流if為

式中：

由式（11）～（13）可知，考慮電弧產生的非線性影響，故障暫態仍為衰減的振蕩過程。

2.2 低阻接地

當發生接地故障時，過渡電阻小于工頻下系統容抗的1/10稱為低阻接地，諧振接地系統發生低阻接地故障時，消弧線圈等效阻抗遠大于并聯的對地分布電容容抗，暫態過程主要為線路的線模、零模電感與對地電容間的串聯諧振，通常忽略消弧線圈對故障暫態過程的影響進而簡化分析[15]。結合復奇頻電壓源串聯電弧模型，得出簡化等值電路如圖7所示。

圖7 低阻接地時的電弧接地故障等值電路Fig.7 Equivalent circuit under arc grounding fault with low resistance

對圖7所示模型建立二階微分方程，可求得低阻接地時原故障暫態為衰減的振蕩過程。與第2.1.2節同理，可得僅考慮故障虛擬電源作用時的if0與包含全奇頻次諧波的故障暫態零模電流if分別為

同樣，考慮電弧產生的非線性影響，故障暫態仍為衰減的振蕩過程。由所建模型與式（15）可知，隨著疊加電壓源頻次不斷增加、幅值不斷減小，高頻次電壓源產生的零模電流亦不斷減小，即高頻次諧波電源對故障原有暫態的影響逐漸減弱，這也從側面反映了在工程實際問題中多以中頻、低頻段特征為主要分析部分的合理性。

由上述分析可知，電弧會向原有故障電流中疊加了其他頻段信息，在一定程度上改變了原故障電流波形形態，但考慮原故障虛擬電源與電弧模型等效電源幅值差異與頻率差異，電弧對原有固定過渡電阻故障暫態主諧振過程的影響較弱。從工程應用角度來看，適用于諧振接地系統固定過渡電阻接地的暫態保護算法（例如，利用不同出線電壓、電流波形相似性等）仍適用于電弧接地故障。

此外，本文所提暫態分析方法使用的簡化模型基于控制論電弧靜態特性模型與傅里葉級數理論，比較適用于工程應用。由表1可知，各類電弧模型諧波含量雖差別不大，但由于假定條件、適用場合均有所不同，在應用本文方法分析時，亦可通過調整各頻次諧波在簡化模型中對應的幅值系數實現如式（9）～（15）所示的計算，適應性較強。

3 穩定電弧接地故障辨識原理

現有電弧接地故障辨識多依賴于人工神經網絡、支持向量機、模糊理論、小波變換等單一或多種算法相結合的方法[16-19]，主要對電弧電流奇異信號即諧波進行檢測。但受實際故障環境中溫度、濕度、風速等條件影響，當發生電弧接地故障特別是低阻接地電弧電流較大時，可能存在電弧電流零休過程不夠明顯，奇異性不易檢測等問題。

近年來，在電網企業推廣應用的一次、二次融合成套設備，具備了零序電壓、電流的采集功能，為配電網單相接地故障的檢測創造了技術載體。由于電弧電壓諧波含量一般遠遠大于電流諧波含量[8]，將電弧電壓信息與電流信息結合后進行故障類型辨識，其辨識準確度顯然優于僅利用電流信息進行辨識的相關算法。

由分析可知，當發生穩定的電弧低阻接地故障時，故障點處的電弧電壓主要由基波與3次、5次、7次等奇次諧波構成。各頻次諧波在線路上逐漸衰減，其衰減特性受線路參數影響，理論上各不相同。但考慮到實際配電線路長度一般較短，加之受電壓互感器傳變精度與設備采樣精度等因素影響，故在工程應用中，各頻次諧波的衰減特征差異可忽略不計。

因此，當發生電弧低阻接地故障后，將故障線路上游各電壓獲取點的故障相電壓或零序電壓進行傅里葉分解，可得其主要奇次諧波（7次諧波以內）對應函數式的幅值常量系數比值與故障點處的幅值常量系數比值近似相等，該比值近似等于3次諧波∶5次諧波∶7次諧波=1/3∶1/5∶1/7，由于電弧電流非線性，則高阻接地時該比例可能稍有差異。該特征可作為電弧接地故障類型辨識的輔助判據之一（簡稱為電壓判據），與現有辨識算法判據（簡稱為電流判據）相結合以提高相關辨識準確度。以故障相電壓為例，其辨識的主要步驟如下（零序電壓情況類似）。

步驟1接地故障發生后，當零序電壓大于算法啟動門檻值時，算法啟動，首先利用故障電氣參量進行故障選相。

步驟2計算不同位置的故障相電壓各頻次諧波含量比值（主要是基波與3次、5次、7次諧波），以及相關電流判據所需的各項參數。

步驟3對各項參數與數據進行集中對比，判別多個周期內的各項參數是否分別滿足電壓、電流判據的誤差裕度要求。該裕度會影響算法處理除電弧電阻外的固定過渡電阻的能力。

步驟4根據辨識準確度要求，給出辨識結果。

4 仿真與現場數據驗證

4.1 仿真模型

在Matlab/Simulink中建立典型10 kV諧振接地配電網仿真模型如圖8所示。其中，消弧線圈LP經接地變壓器接入系統，其過補償度為8%；系統包含3條純電纜線路（出線L2，L3，L4），1條架空電纜混合線路（出線L1），1條純架空線路（出線L5），并假定出線L4中間有一處三相電壓及電流獲取點P，各出線口有三相電壓及電流獲取點N1～N5。各段線路的長度、類型及電弧接地故障發生位置等信息見圖8。不同類型線路阻抗參數見表2。主變壓器參數設定為額定電壓比UN1/UN2=110/10.5、額定容量SN=50 MV·A、空載損耗P0=35 kW、短路損耗Pk=205 kW、短路電壓比為10.5%、空載電流比為0.52%。另外，根據文獻[8，10]的研究成果，結合本文搭建仿真模型的具體參數，利用控制論電弧模型仿真電弧接地故障，其參數設置為初始迭代電導g0=10 000 S、Is=3.34 A、Vs0=45 V/cm、l=1 cm、β′=7.5×10-6。

圖8 諧振接地系統仿真模型示意Fig.8 Schematic of simulation model of Peterson coil grounded system

表2 仿真模型線路參數Tab.2 Line parameters of simulation model

4.2 簡化電弧模型與動態模型故障過程對比

圖9給出了當相電壓達到最大值時發生3種電弧接地故障，分別采用控制論電弧靜態特性模型與受控源模型的故障點電流對比情況。其中，控制論電弧使用圖8所示拓撲的分布參數模型，受控源電弧使用對應系統的故障復合等值電路。

圖9 不同接地情況下電流波形對比Fig.9 Comparison of current waveform under different grounding conditions

可見，兩種方法的故障電流動態過程稍有差異，但主要特征可認為近似相同，即在誤差允許的范圍內，為提高傳統故障等值電路在計算電弧接地故障時的能力，可以將動態電弧模型轉化為靜態模型并得出相應的定量計算分析結果，驗證了本文對電弧接地故障暫態過程的分析方法的正確性。

4.3 電弧接地故障辨識原理驗證

利用圖8所示諧振接地系統仿真模型及控制論動態電弧模型進行電弧接地故障辨識算法驗證，對波形數據進行傅里葉分解，可得電弧低阻接地（10 Ω）時不同故障點、監測點的故障相電壓主要奇 次諧波對應函數式的幅值常量系數如表3所示。

表3 故障相電壓主要頻次諧波的幅值常量系數Tab.3 Amplitude coefficient of main frequency harmonics of fault phase voltage

經傅里葉分解后，此時故障點3次、5次、7次諧波對應函數式的幅值常量系數分別約為0.333 1∶0.211 4∶0.141 7。結合表3數據可知，在系統發生電弧低阻接地故障后，母線或線路上的故障相電壓各奇頻次諧波含量比值與故障點處的各奇頻次諧波含量比值近似相等，驗證了本文利用母線及線路電壓進行電弧故障類型辨識原理的正確性。

4.4 現場數據驗證

通過仿真驗證可知，電弧黑盒模型與本文所用靜態模型對電弧接地故障的動態模擬差異不大，可以將動態電弧模型轉化為靜態模型并得出相應的定量計算分析結果。通過現場數據進一步驗證本文的簡化模型較傳統線性過渡電阻模型的優越性。

在FJ省LY市110 kV變10kV的HB站HY線進行人工接地實驗，實驗變電站中性點經消弧線圈接地，HY線所在Ⅰ段母線共有7條線路投入使用。將現場記錄的經2.5 mm球隙（過渡電阻為10 Ω）接地故障電流波形與本文所提簡化模型、傳統線性過渡電阻模型分別進行對比，如圖10（a）～（b）所示。

圖10 現場實驗波形與模型仿真波形對比Fig.10 Comparison between field waveform and simulation waveforms

對比故障后的電流暫穩態電氣量特征可知，本文所提簡化分析模型對現場暫穩態電流的模擬精度均優于傳統的線性過渡電阻模型，更接近原故障錄波。同時，簡化分析模型表現為獨立電壓源串聯形式，可結合疊加原理與原等值電路求解思路定量計算各故障電氣量，在不增加分析復雜度的同時，能較好體現電弧非線性特征的影響，具有一定優越性。此外，將以上兩次電弧接地實驗所獲取的母線處故障相電壓做傅里葉分解，其中3次、5次、7次諧波對應幅值常量系數的比值分別約為0.332 2∶0.189 8∶0.129 4與0.334 6∶0.195 4∶0.131 8，可驗證本文所提電壓判據的有效性。

5 結語

針對線性過渡電阻等值電路在模擬電弧非線性特征方面的局限性，本文合理簡化電弧黑盒模型，結合故障復合等值網絡，提出一種諧振接地系統電弧接地故障暫態分析方法，并定量計算高阻接地過阻尼、高阻接地欠阻尼及低阻接地等情況下弧光接地的暫態電流解析表達式，有效提高了原故障等值電路分析計算電弧接地故障的能力。同時，根據電弧電壓諧波衰減特性，提出一種綜合電弧電流與線路電壓信息的穩定電弧接地故障辨識原理。通過對比不同過渡電阻的簡化電弧模型與傳統線性過渡電阻模型、電弧黑盒模型的故障電流特征以及不同電弧接地故障位置的線路電壓諧波含量，驗證了本文簡化模型、故障類型辨識算法的正確性，為后續諧振接地配電網電弧接地故障保護的研究提供了相關的理論依據。