帶Allee效應的混合單種群模型解的存在性

張彩琴，郭琳琴

(呂梁學院 數學系，山西 離石 033001)

的解的存在唯一性。

0 引言

帶有Allee效應[1]的隨機微分方程在不同種群的生存分析中有著廣泛的應用，進而受到國內外學者的廣泛關注[2-5].文獻[6]研究了單種群間的競爭系統(1):

(1)

其一般化為(2):

(2)

當θ=1時，(2)退化為(1).文獻[7]提出如下帶有Allee效應的模型(3):

(3)

文獻[7]考慮到環境對模型的影響，給出了帶有隨機擾動的模型(4):

(4)

但模型(4)中的白噪聲只能刻畫小型的波動對種群的影響，對于自然界中大型的、災難性的沖擊等可以通過有色噪聲來進行表示，文獻[8]對方程(5)：

(5)

的生存情況進行分析.

受上述文獻的啟發，本文將研究下列方程：

(6)

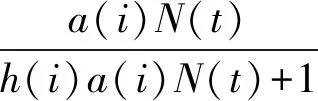
1 預備知識

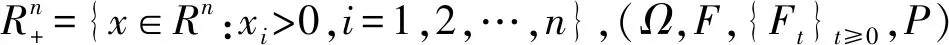
假設條件

(H1)ξ(t)是Ft適應的且獨立于布朗運動；

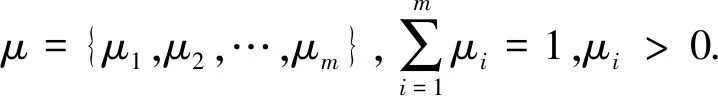
(H3)令C2(Rn;R+)表示Rn上所有二階連續可微的非負函數V(x)的集合.對于任意V∈C2(Rn;R+)，若(x(t),λ(t))是方程(7)：

dx(t)=f(x(t),λ(t))dt+g1(x(t),λ(t))dB1(t)+g2(x(t),λ(t))dB2(t)

(7)

的解，則可定義算子：

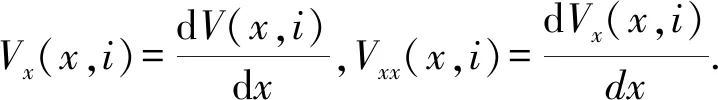
2 主要結果

定理給定初值(N(0),ξ(0))∈(0,+∞)×M，方程(6)存在唯一解(N(t),ξ(t))∈ (0,+∞)×M,t≥0.

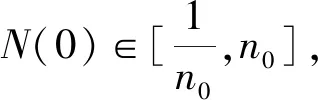
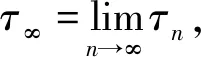
系統(6)的系數滿足局部Lipschitz條件，由文獻[9]中的定理3.15知，系統(6)存在一個唯一局部解N(t)(t∈[0,τe))，若τe=∞意味著方程(6)有全局解.下證τe=∞.

假設τ∞=∞不成立，即P{ω:τ∞(ω)=∞}≠1，則P{ω:τ∞(ω)=∞}<1，即P{ω:τ∞(ω)<∞}=1-P{ω:τ∞(ω)=∞}>0，因此，?T>0,ε∈(0,1)，n≥n0使得P{τ∞≤T}>ε，故P{τn≤T}≥ε.

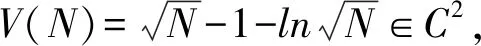
(8)

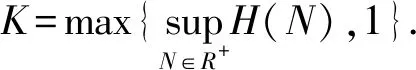
對式(8)兩端積分取期望可得：

EV(N(τn∧T))≤V(N(0))+KE(τn∧T)≤V(N(0))+KT.

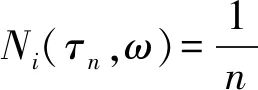
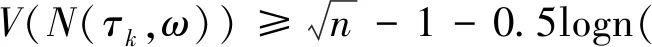
所以

(9)

式(9)兩端取極限t→∞得：

∞>V(N(0))+KT>∞

矛盾，故有τ∞=∞，即τe=∞.

3 結束語

本文研究了帶Allee效應的隨機微分方程(6)的解的存在唯一性，推廣了文獻[8]中的結果.