基于差分法的水波動畫模擬

楊 艷，范示示，王艷永

(呂梁學(xué)院 數(shù)學(xué)系，山西 離石 033001)

水波動畫的模擬主要分為三類[1]：第一類是基于波的分析方法，其中最簡單的一種是用正弦函數(shù)來進(jìn)行仿真，模擬水波表面.這種方法只是從形態(tài)上模擬了水波的特性，并沒有考慮水波在運動過程中外部與內(nèi)部環(huán)境以及其他現(xiàn)實因素的影響.第二類是基于粒子的分析，將流體看作是離散的粒子集，每個粒子按照一定的規(guī)則不斷的運動.第三類是基于物理模型的方法，研究流體的運動，最典型的是通過求解粘性不可壓縮流體的動量守恒方程：Navier-stokes方程，得到流體完整的速度場.

本文采用二維水波方程，設(shè)定水滴落下的初值條件，得到方程的差分解，并且通過穩(wěn)定性討論，得到參數(shù)的取值范圍，模擬水面蕩漾動畫.

1 模型的建立

本文選用二維水波方程[2]：

(1)

(1)式中z表示水面高度，x,y為空間變量，t為時間變量，其中c、μ均是非負(fù)的常數(shù)，c表示單位時間內(nèi)水波位移的距離，μ表示流體的黏度.

由于在模擬水滴湖面波動的過程中，波面是從滴落位置(x0,y0)開始呈直徑為w的圓環(huán)擴(kuò)散的，在垂直方向的最大位移為h.為了能夠產(chǎn)生水滴湖面造成的湖面的波動這一狀態(tài)，先獲取湖面下落的初始圓環(huán)的高度h和寬度w，設(shè)定:

(2)

為方程的初始條件，表示圓環(huán)內(nèi)部曲面向下凹陷，同時圓環(huán)外水面的垂直位移都為零，如圖1.

圖1 初始條件圖像

同時初值條件包括:

(3)

邊界條件選取

(4)

2 差分法求解模型

將區(qū)間[a,b]和[c,d]分別n等分，步長分別為Δx,Δy(為了討論方便，取方形區(qū)域，此時記相同步長為Δd)，得到空間結(jié)點(xi,yj)(0≤i≤n,0≤j≤n).令Δt為時間步長，并用z(xi,yj,tk)表示tk時刻點(xi,yj)的水面高度.

2.1 方程的離散

將方程(1)中各個導(dǎo)數(shù)用如下二階格式離散，

(5)

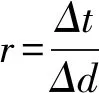
(6)

代入(5)式整理，得方程的差分解為:

(7)

2.2 初始條件的離散

將

舍去誤差項，代入初始條件(3)，得:

(8)

(7)式中取k=0，得：

將(8)式代入整理，得:

(9)

綜合(7)式和(9)式，得方程的差分解為:

(10)

3 解的穩(wěn)定性分析

黏性阻尼力μ為與溫度有關(guān)的量，可以通過經(jīng)驗得到，數(shù)量級為10-3.為了討論穩(wěn)定性，需確定波速c和Δt的關(guān)系.

故

(11)

由(6)式，得a2>0,a3<0(由于μ為10-3，Δt取充分小，即假設(shè)μΔt≤2)，故：

此時，(11)式可寫為：

假設(shè)a1>0，即：

(12)

又由于a2>0，上式可寫為：

同理，k=0,1,2,…時，由(7)式可得：

(13)

故有：

記，

要使(13)式穩(wěn)定，需矩陣A的譜半徑ρ(A)≤1+C0Δt,其中C0為常數(shù).

進(jìn)一步計算A的特征值為：

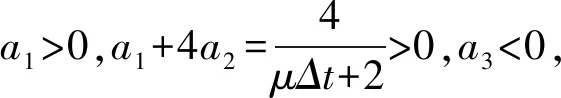
以下證明存在常數(shù)C0，使得ρ(A)≤1+C0Δt，即存在常數(shù)C0，使

用反證法，假設(shè)對于認(rèn)識常數(shù)C0，都有

成立，按C0降冪整理得：

Δt2(μΔt+2)2C02+2μΔt2(μΔt+2)C0+2μ2Δt2-8<0，

4 模擬結(jié)果

圖3 波面蕩漾開畫面

圖4 整個水域波動

圖5 水面趨于平靜

以上四幅圖是隨著時間增加，水面的各個不同時間運動圖，從水滴反彈到波面趨于平靜的狀態(tài).

5 結(jié)束語

通過有限差分法求解二維的水波方程，模擬了隨機(jī)的水滴滴落從而引起湖面波動的動畫.討論了滿足穩(wěn)定條件的參數(shù)取值范圍，并分析了初值和邊界值的選取.結(jié)果表明，該方法可以真實的模擬水滴湖面波動的現(xiàn)象.本文是作為本科生的數(shù)值分析課程的擴(kuò)展實驗項目.在文獻(xiàn)[2][3]中均有類似討論，創(chuàng)新點是從數(shù)學(xué)角度對穩(wěn)定的條件進(jìn)行推導(dǎo).下一步工作類似于文獻(xiàn)[2][3]，可以結(jié)合計算機(jī)圖形學(xué)課程光照模型，使得動畫具有真實感，提高學(xué)生實驗?zāi)芰?