讓函數考查回歸本質*
——對廣州市中考數學第25題的思考

廣東省東莞市東莞中學松山湖學校(523808) 嚴 明

廣州市中考數學第25 題的設計一直以來都頗具特色,近二年來,都是以含參二次函數為主體,無圖呈現的綜合壓軸題,解決這類問題應當如何尋找思路的突破口? 給我們的教學帶來怎樣的思考? 本文以2019 年、2020 年的問題解答為例,談些自己的思考,供大家參考.

1 2019 年原題呈現

已知拋物線G:y=mx2?2mx ?3 有最低點.

(1)求二次函數y=mx2?2mx ?3 的最小值(用含m的式子表示);

(2)將拋物線G向右平移m個單位得到拋物線G1.經過探究發現,隨著m的變化,拋物線G1頂點的縱坐標y與橫坐標x之間存在一個函數關系,求這個函數關系式,并寫出自變量x的取值范圍;

(3)記(2)所求的函數為H,拋物線G與函數H的圖象交于點P,結合圖象,求點P的縱坐標的取值范圍.

1.1 思路分析

函數綜合題不給出函數圖象,這對考生無疑構成為一種強大的心理壓力, 需要他們冷靜分析試題中的每一個條件,根據解題的需要,自行繪制出函數的圖象,運用數形結合的方法分析問題.

對于此題的題干條件,含參數m的二次函數有最低點,可以判定二次項系數m ＞0,在第(1)中求二次函數的最小值,可以運用公式法,也可以運用配方法,而運用配方法將函數解析式轉化成頂點式更好.

第(2)問中,將拋物線平移,根據坐標系平移特征,平移m個單位后拋物線G1可以表示,其頂點坐標也可以表達,利用消元思想求函數解析式.

第(3) 問, 研究拋物線G與一次函數H之間的交點P, 一般思路是將兩函數解析式聯立組成方程組,解方程組, 但面對一個含參的方程組, 消元后, 得到:mx2+ (?2m+ 1)x ?1 = 0, 在不能使用因式分解的情況下接下來要用公式法解,計算量顯然會很大,是不是要硬著頭皮進行呢? 一時思維受阻.根據題目提示:“結合圖象,判定點P的縱坐標的取值范圍”,嘗試性地畫函數圖象,但由于拋物線G含有參數m,圖象似乎也很難準確確定.

當然,還是可以確定一些相關要素的,比如拋物線對稱軸為x= 1,與y軸交點坐標C(0,?3),畫出示意圖等.觀察圖象,可知拋物線過點C的對稱點D(2,?3),得到交點P的縱坐標肯定小于?3,而大于?m ?3,但接下來要更精確地鎖定點P縱坐標的取值范圍,這是有一定挑戰的,發現點E,借助于點E的縱坐標是關鍵.

1.2 解答參考

(1)由題意得:y=mx2?2mx ?3=m(x2?2x)?3=m(x ?1)2?m ?3,∵拋物線有最低點,∴m ＞0,二次函數的最小值為?m ?3.

(2)由題意得,G:y=m(x ?1)2?m ?3 向右平移m個單位后得G1:y=m(x ?1?m)2?m ?3(m ＞0),∴頂點坐標為(1+m,?m ?3),則消去m,得y=?x ?2,∵m ＞0,∴x=1+m ＞1.即隨著m的變化,頂點的縱坐標與橫坐標之間存在的函數關系式為:y=?x ?2,且取值范圍是x ＞1.

(3)由y=mx2?2mx?3可知: 對稱軸為x=1,與y軸交點坐標為C(0,?3),由拋物線的對稱性可知,其圖象必過對稱點D(2,?3).∴拋物線的頂點坐標為(1,?m ?3),對于函數H:y=?x ?2(x ＞1),當x=1 時,y=?1?2=?3,∴點F(1,?3),當x=2 時,y=?2?2=?4,∴E(2,?4),∴函數圖象交點P必在線段EF之間,即點P縱坐標yP取值范圍是:?4＜yP ＜?3.

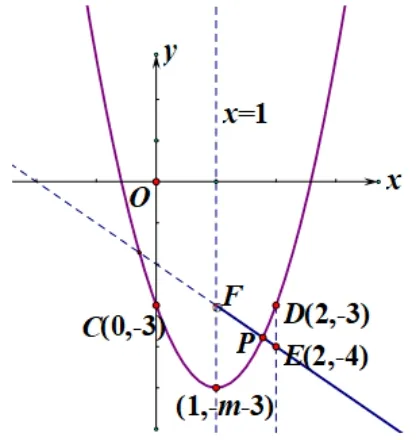
圖1

2 2020 年原題呈現

在平面直角坐標系xOy中,拋物線G:y=ax2+bx+c(0＜a ＜12)過A(1,c ?5a),B(x1,3),C(x2,3),頂點D不在第一象限,線段BC上有一點E,設ΔOBE的面積為S1,ΔOCE的面積為S2,S1=S2+

(1)用含a的式子表示b;

(2)求點E的坐標;

(3)若直線DE與拋物線G的另一個交點F的橫坐標為+3,求y=ax2+bx+c在1＜x ＜6 時的取值范圍(用含a的式子表示).

2.1 思路分析

這也是沒有圖形呈現的函數綜合題,需要仔細分析問題題干中給出的條件,盡可能地尋找問題的突破口.

第(1)問要用含a的式子表示b;二次函數解析式含a、b、c三個參數,所給的A、B、C三點坐標也都殘缺不全,剛開始真的并不一定很明確要如何走, 但可以嘗試著將點A的坐標代入解析式,結果運氣好化簡時消去了c,得到一個關于a、b的關系式,問題得到解決;

第(2)問是在第(1)基礎上進一步研究.題目已知中C,B兩點的橫坐標不確定,但縱坐標相同,可知B、C兩點是拋物線上關于對稱軸對稱的點,(1)的結論,實質是研究拋物線的對稱軸,得到對稱軸為x= 3,再研究ΔOBE、ΔOCE的面積,這是兩個不同底,但高都為3 的三角形,由題目中S1、S2的關系式,可轉化得到BE=CE+1,如何認識這個關系式是一個難點,可放在數軸上,也可由線段及中點的知識推導.

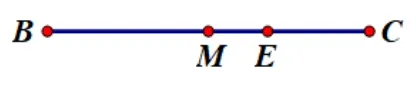
圖2

如圖2, 線段BC及中點M, 得到BM=MC, 由BE=EC+1,∴BM+EM=EC+1,∴MC+EM=EC+1,∴MC+EM ?EC= 1,∴EM=在坐標系中,點M坐標為(3,3),由此推理得到點E的坐標,當然,需要注意的是點B不一定在左邊,所以點E的位置在坐標系中,可能在對稱軸右邊,也可能在左邊,分二種情況;

第(3)問,肯定是問題的制高點,首先還是要確定一下圖象,哪怕是某些元素不確定的大致圖象,這一問中,點D是頂點,點F的橫坐標說明點F在對稱軸右邊,所以點E只能是對稱軸右邊點,接下來如何思考呢? 由D、E、F三點的橫坐標都已確定或可表示,所以,思考這三點的縱坐標,構造由平行線組成的兩三角形相似來尋找突破口,經過比較大的運算之后,可得到c、a之間的關系式c= 9a,這樣二次函數解析式就可以都用含a的式子表示,再由對稱軸為x= 3,研究1＜x ＜6 可知,這是需要研究拋物線上非對稱區間y的取值范圍,分別求出界點(即x=1、x=6 時)對應的函數值,再綜合得到函數值的取值范圍.

2.2 解答參考

(1)由A(1,c ?5a)代入解析式y=ax2+bx+c,得到:a+b+c=c ?5a,∴b=?6a;

(2) 由題意, 可得對稱軸x== 3; 再由B(x1,3),C(x2,3) 可知:BC//x軸, 且關于對稱軸對稱.由S1=∴EB=CE+1,再由對稱性可知,點E到對稱軸的距離為

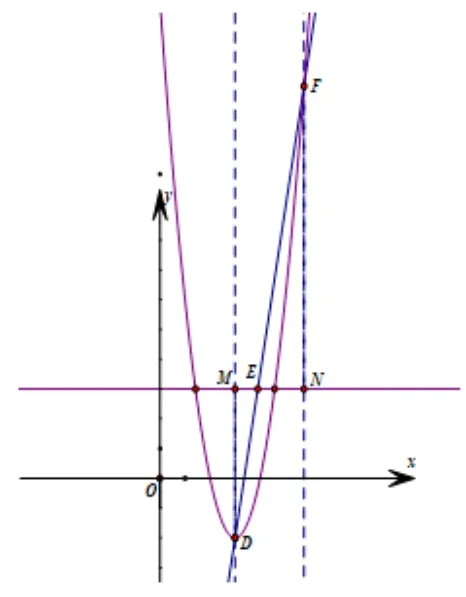
圖3

(3) 由交點F的橫坐標為+ 3＞3, 可 見點F在對稱軸右邊, 如圖3,過點F作FN ⊥x軸交于直線BE于點N, 當x=時,y=?6a×∴FN=?9a+c ?3,EN=由(1)可知,當x=3 時,y=9a?18a+c=c?9a.∴D(3,c?9a),MD=3?c+9a,由題意, 可得: ΔMDE∽ΔFEN.得到:化簡得到c=9a,∴拋物線的解析式為y=ax2?6ax+9a,∴由1＜x ＜6,a ＞0,對稱軸為x= 3,可知: 當x= 3 時,y最小為c ?9a= 0;當x= 6時,y=36a ?36a+c=9a,∴0 ≤y ＜9a.

3 試題思考

3.1 關注函數壓軸考查回歸本質

長期以來, 充斥于中考卷中二次函數類的綜合壓軸題,大都是把函數圖像與幾何圖形結合起來, 考查圖形的屬性,這類試題因其過分注重技巧套路,有將未來高中要學的解析幾何的有關研究放在初中探究傾向,不夠自然,偏離了函數研究的本質,其命題導向一直飽受詬病.什么是函數? 函數就是刻畫現實世界運動變化規律的一種數學模型,在初中范圍內,函數本質是“變量說”,指向的是兩個變量之間的一種單值對應關系,而函數的單調性,才是中學學習的函數最基本、最核心的性質,所以,在初中數學領域,最重要的知識就是函數的概念、圖像和性質,最重要的思想就是模型思想、變化和對應的思想.考查的重點就是利用數形結合的研究方法,既從解析式來確定圖像的意義,又從圖像來獲取對應與變化規律.廣州市這二年函數綜合題可謂是正本清源,回歸本質.從所涉及到的知識點來看,主體是二次函數,專注于二次函數的頂點、對稱軸、交點坐標、函數圖象平移特征等基礎知識,前一題從拋物線頂點坐標變化規律的角度,研究縱坐標與橫坐標兩個變量之間的對應關系,并應用函數圖象,直觀想象研究交點縱坐標的變化規律;而后一題,則以圖像上若干點的坐標之間的依賴關系, 研究拋物線上一部分的變化規律.這種考查抓住了函數的本質,體現了知識之間內在聯系.

3.2 回應當下的命題趨勢

函數中含參問題是近年來各地中考數學試題的一個亮點.研究這兩年各地的中考試題, 不難發現, 以含參數的形式來研究數學問題有增多趨勢,比如2019 年的揚州卷第27題、宜昌卷第24 題、泰州卷第26 題、天津第25 題、浙江舟山卷第24 題,2020 年上海第24 題、北京第26 題、長沙第24題、揚州第28 題等.其實,廣州卷早在2016 年中考中就有類似的設計,在2018 年中考卷第24 題也是如此.參數問題,因其抽象不具體、參變量不確定而引起圖像相應地產生某些變化特征,對學生解題能力要求較高,一直以來都是學生不易把握的難點,但同時,這也是初、高中知識銜接的一個切入口,廣州卷堅持這種導向,既是對當下命題亮點趨勢的一種回應,也是對教學導向的一種堅守.

4 教學啟示

4.1 堅持數學學科核心素養的深度教學

從數學學科核心素養的角度,文中的兩道綜合題都是重點考查了學生的數學運算、邏輯推理、直觀想象、數學抽象等核心素養.首先是學生的運算能力.解決有關綜合題,沒有高超的運算能力,肯定是行不通的.而參數的加入,使得運算要求變得更高了.含參的頂點坐標、含參的交點坐標、含參的點的坐標、含參式子的因式分解等等,都會增加運算的難度,影響學生運用運算結果進行推理、歸納和發現,阻隔學生的思維,當然這也說明,在初一初二的代數教學中,其實也需要適當滲透一些字母運算的機會的.

其次是數形結合的研究方法受到了挑戰, 參數的加入,使得連畫函數圖像都成了一件很困難的事情,題目中沒有圖像呈現,自然就會影響到學生觀察圖像,直觀想象的能力.由此,在平時的教學過程中,仍然要立足數學學科的核心素養,堅持抓住函數本質的教學,運用圖形和空間想象的意識,發展學生的數學抽象,邏輯推理,規范表達,形成學生一般性思考、程序化思考問題的習慣,發展學生的思維.

4.2 加強含參二次函數解題反思

對于含參數的二次函數綜合題難度往往很大,但也有其相應的學習方法.首先是在日常教學中,教師要引導學生深入探究問題的本質特征,提高解后反思,比如追問“三個一”即一題多解、一題多變、多題歸一,“你知道一道與它有關系題目嗎? ”“你能在別的什么題目中利用這個結果或這種方法嗎? ”而不是盲目追求解題的數量.其次,要深刻理解含參數的二次函數中各參數的含義,克服因參數的不確定性帶來的困難,尋找其變化中的不變量,這通常就是問題的切入點.比如可以嘗試通過含參的二次函數的解析式進行“圖像六追”: 拋物線的開口方向有沒變化、對稱軸有沒有變化、頂點坐標有沒有變化、增減性有沒有變化、有沒有過某個定點、與坐標軸的交點坐標有沒有變化等,從中挖掘其中的隱含信息,尋找不變量,把握圖像的變化規律,并注意積累解題經驗.實際上,對于含參的二次函數y=ax2+bx+c,如果a、b、c之比為定值時,與x軸的交于定點;如果a、b的比為定值時,對稱軸或頂點橫坐標一定不變;解析式如果能夠因式分解成兩個一次式的乘積,就意味著對稱軸以及與x軸兩交點間的距離可研究,觀察解析式,看有沒有哪組值代入,剛好令相關參數全部消除,這就說明圖像過某個定點.