有關三角形的內心與外心基本圖形探究

湖北省武漢市魯巷中學(430074) 熊 燕

初中數學中幾何知識涉及面廣、知識點多,幾何圖形紛繁復雜、千變萬化,一直以來都是初中生學習的重點和難點.然而復雜的幾何圖形往往卻是由一些簡單的基本圖形組合而成.初中數學教材中有不少內涵豐富、具有很強探究性的基本圖形,如果能進一步有效挖掘,不但能鞏固基礎知識,增強學生變式能力,提高數學素養,還能培養學生的抽象思維、邏輯思維、形象思維、發散思維和創新思維.因此,筆者在日常教學中有意識地對一些基本的幾何圖形模型進行提煉和探究,并對這些基本的圖形模型和基本結論的應用進行專題訓練,以提高學生解決幾何綜合題的能力.

1 經典習題展示

練習1.(2013 年武漢市元月調考第10 題) 如圖1, 點I和O分別是ΔABC的內心和外心, 則∠AIB和∠AOB的關系為( )

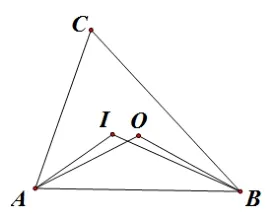
圖1

A.∠AIB=∠AOB

B.∠AIB /=∠AOB

C.2∠AIB ?=180°

D.2∠AOB ?=180°

簡解點O是ΔABC的外心, 所以∠C=又因點I是ΔABC的內心, 所以∠IAB=進而得到結論.

評析遇到三角形的外心,聯想到圓心角與圓周角的兩倍關系,遇到三角形的內心,聯想到內心的定義,即三條角平分線的交點,進而靈活運用相關性質解決數學實際問題.本題主要考查圓周角定理和三角形內心和外心的相關性質,以及三角形內角和定理,解決初中數學中的計算問題.

練習2.(人教版九年級上冊教材習題24.2 第14 題)如圖2,在RtΔABC中,∠C= 90°,AB、BC、CA的長分別為c、a、b,求ΔABC的內切圓半徑r.

簡解一如圖2, 過點O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F, 連接OA,OB,OC.因為圓O是三角形的內切圓, 所以OD=OE=OF=r, 又因為SΔABC=SΔAOB+SΔBOC+SΔAOC=在RtΔABC中,SΔABC=所以進而得到結論

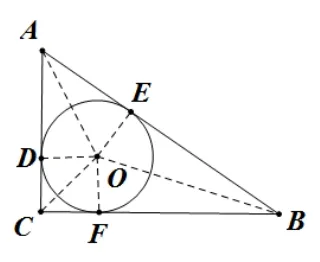
圖2

簡解二如圖2, 過點O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F, 則∠ODC=∠OFC= ∠C= 90°, 所 以 四邊形ODCF是矩形, 又因為OD=OF, 所以四邊形ODCF是正方形, 由切線長定理可知,AD=AE,CD=CF,BF=BE, 所以BC+AC ?AB= 2CD= 2OD, 即a+b ?c= 2r,進而得到結論r=

補充如圖3 求RtΔABC的外接圓半徑R.

簡解取線段AB的中點G,連接CG, 在RtΔABC中,AG=BG=CG=A、B、C三點在以點G為圓心的圓上,所以圓G是ΔABC的外接圓,其半徑R=

圖3

評析遇到直角三角形的內心問題,聯想到三角形面積公式和切線長定理,善于運用割補法計算三角形的面積,遇到直角三角形的外心問題,聯想到“直角三角形斜邊上的中線等于斜邊長的一半”和“三點共圓”等初中數學幾何性質,解決數學問題.本題通過兩種不同的解法, 得到直角三角形內切圓半徑r的兩個數學表達式, 其本質是一樣的.(注: 要證r=成立, 只需證(a+b+c)·(a+b ?c) = 2ab成立, 即證a2+b2=c2成立,以上結論顯然成立)本題是對教材上的習題的再創造,充分體現新課程標準中數學試題來源于教材又高于教材.

練習3.(人教版九年級上冊教材復習題24 第13 題) 如圖4, 點E是ΔABC的內心,AE的延長線和ΔABC的外接圓相交于點D.求證:DE=DB.

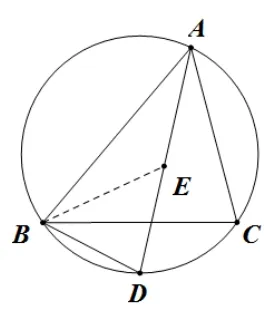
圖4

簡解連接BE, 因為點E是ΔABC的內心, 所以∠DAC= ∠DAB, ∠ABE= ∠CBE, 又因為弧CD=弧CD, 所以∠DAC= ∠DBC, 即∠DAB= ∠DBC, 又∠DBE= ∠DBC+∠CBE, ∠DEB= ∠DAB+∠ABE,所以∠DBE=∠DEB,進而得到結論DE=DB.

評析初中數學幾何中遇到三角形的內心,聯想到內心的定義,即三條角平分線的交點,進而靈活運用相關性質解決數學實際問題.本題根據內心定義和圓周角的相關性質,解決初中數學幾何中的證明問題.

2 基本圖形提煉

基本圖形一:如圖5,ΔABC中,∠A=α,點I是ΔABC的內心,則∠BIC=90°+如圖6,ΔABC中,∠A=α,點O是ΔABC的外心,則∠BOC=2α.

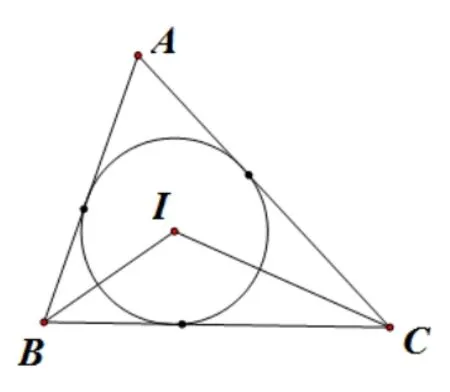
圖5

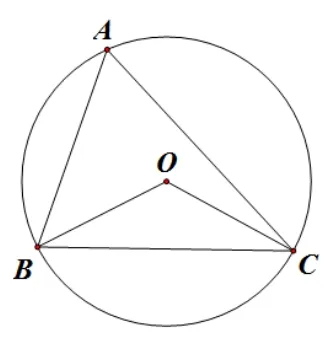
圖6

基本圖形二: 如圖7, 在RtΔABC中,∠C=90°,⊙O為ΔABC的內切圓, 切點分別為D、E、F,若邊BC、CA、AB的長分別為a、b、c, 則ΔABC的內切圓半徑r=外接圓半徑

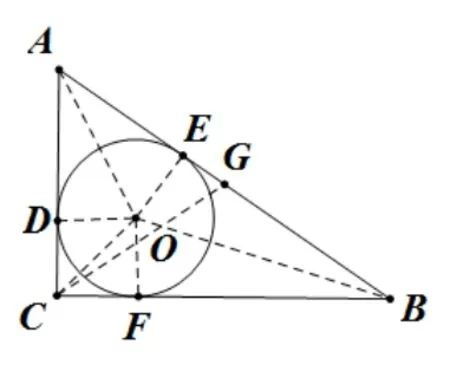
圖7

推廣: 如圖8, 在ΔABC中, 邊BC、CA、AB的長分別為a、b、c, 先用割補法或雙勾股法求出ΔABC的面積S,再計算ΔABC的內切圓半徑

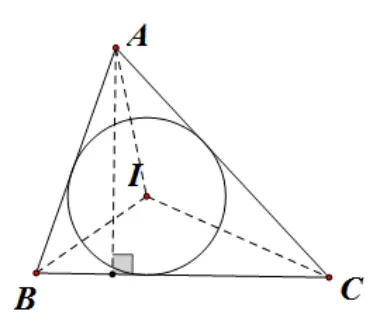
圖8

基本圖形三: 如圖9, 點E是ΔABC的內心,AE的延長線和ΔABC的外接圓相交于點D, 則DE=DB=DC.(B、E、C三點在以D為圓心,DB長為半徑的⊙D上)

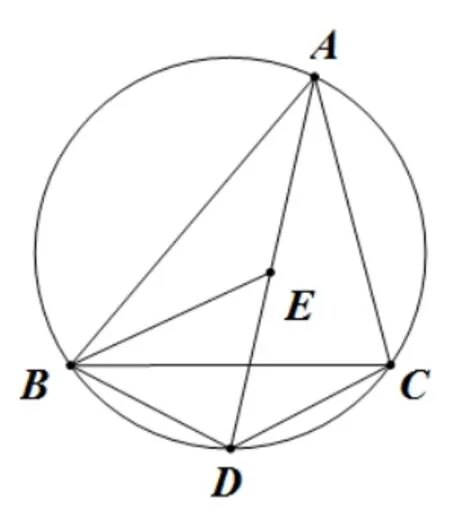
圖9

3 基本圖形應用

例1(人教版九年級上冊教材24.2.2 練習第2 題)ΔABC的內切圓半徑為r,ΔABC的周長為l,求ΔABC的面積.(提示: 設ΔABC的內心為O,連接OA,OB,OC.)

圖10

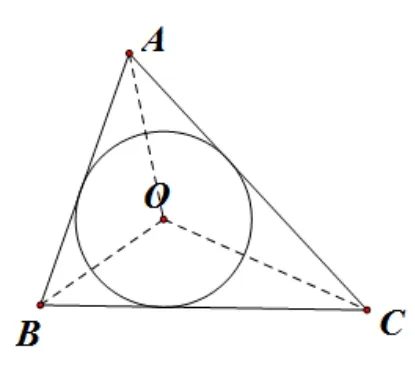
圖11

分析問題中要求解ΔABC的面積,根據上述基本圖形二,很自然地聯想到連接OA,OB,OC,將大三角形分割為三個小三角形,因此,這里采用割補法求面積.

解析如圖11, 設ΔABC的內心為O, 連接OA,OB,OC,則OA=OB=OC=r,SΔABC=SΔAOB+SΔBOC+

評析本題屬于教材中的練習題,主要考查三角形的周長、面積和內切圓半徑之間的數量關系,運用基本圖形二的推廣,可以快速解決.

例2(2019 年武漢市中考第9 題)如圖12,AB是⊙O的直徑,M、N是弧AB(異于A、B) 上兩點,C是弧MN上一動點,∠ACB的角平分線交⊙O于點D,∠BAC的平分線交CD于點E.當點C從點M運動到點N時, 則C、E兩點的運動路徑長的比是( )

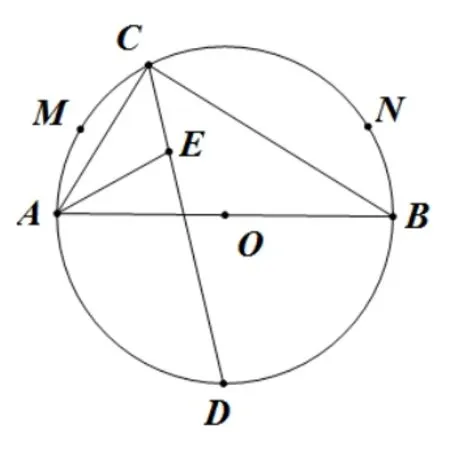
圖12

分析如圖13, 連接EB, 根據上述基本圖形三, 易知點E在以D為圓心DA長為半徑的圓上, 其運動軌跡是弧GF, 點C的運動軌跡是弧MN, 由題意∠MON= 2∠GDF, 再利用弧長公式計算即可解決問題.

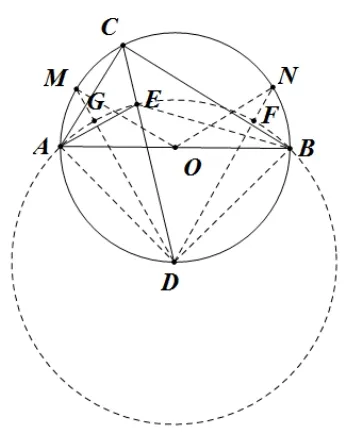
圖13

解析如圖13,連接EB、AD、BD、OM、ON、DM、DN,DM、DN分別與⊙D交于點G、F,設OA=r,則因為AB是直徑,所以∠ACB= 90°,因為CE、AE分別是∠ACB、∠BAC的角平分線,所以E是ΔABC的內心,根據上述基本圖形一,易知∠AEB= 135°.因為∠ACD= ∠BCD,所以弧AD=弧BD, 即AD=BD, 因為AB是直徑, 所以∠ADB= 90°, 所以AD=BD=根據上述基本圖形三, 易知點E在以D為圓心DA長為半徑的圓上, 其運動軌跡是弧GF, 點C的運動軌跡是弧MN, 由題意可知∠MON= 2∠GDF, 設∠GDF=α, ∠MON= 2α, 故弧MN長=弧GF長=所以弧MN長/弧GF長=

評析本題考查弧長公式,圓周角定理,三角形內心的有關性質,解題的關鍵是理解題意,正確尋找到點的運動軌跡,屬于中考選擇題中的壓軸題.

例3(2012 年武漢市元月調考改編)如圖14,BC是⊙O的直徑,半徑為R,A為半圓上一點,I為ΔABC的內心,延長AI交BC于D點, 交⊙O于點E, 作IF ⊥BC, 連接AO,BI.下列結論: ①∠BAE=45°; ②4∠AIB?∠BOA=360°; ③BC=為定值,其中正確的結論有_______.

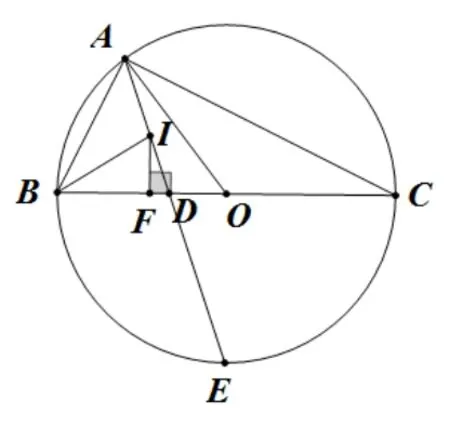
圖14

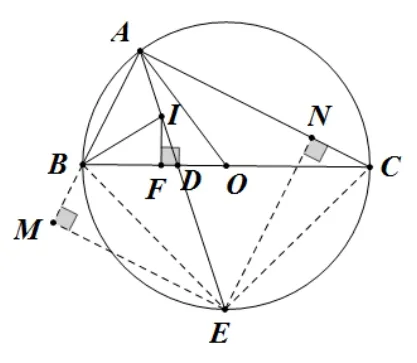
圖15

分析①利用三角形內心的定義解答即可; ②根據上述基本圖形一和圓周角定理可得結論; ③根據上述基本圖形三和等腰直角三角形性質可得正確性; ④過E點作角兩邊的垂線, 可以由三角形全等及等腰直角三角形性質, 得到AB+AC=可得④正確; ⑤根據上述基本圖形二得到直角三角形內切圓半徑公式,再結合④的結論,可證得⑤正確.

解析①因為BC是⊙O的直徑, 所以∠BAC=90°, 又因為I為ΔABC的內心, 所以AE平分∠BAC,即∠BAE= 45°, 正確; ②根據上述基本圖形一, 因為I為ΔABC的內心, 所以∠BIA= 90°+即4∠BIA= 360°+ 2∠C, 又因為∠BOA= 2∠C, 所 以4∠AIB?∠BOA=360°,正確; ③如圖15,連接BE、EC,根據上述基本圖形三,易知BE=EI=EC,因為BC是⊙O的直徑, 所以∠BEC= 90°, 所以BC=正確; ④過點E作EM⊥AB于M,EN⊥AC于N,則四邊形ENAM是矩形,∠ENC= 90°,∠EMB= 90°,由①可知, ∠BAE= 45°, 所以AM=EM, 所以四邊形ENAM是正方形, 所以AM+AN=√EM=EN, 又因為∠CEN+ ∠NEB= 90°,∠MEB+ ∠NEB= 90°,所以∠CEN= ∠MEB, 所以ΔCEN∽= ΔBEM, 所以CN=BM, 所以AB+AC=正確; ⑤根據上述基本圖形二, 易知IF為RtΔABC內切圓半徑,IF=即AB+AC=BC+2IF=2R+2IF,即IF+R=由④可知,AB+AC=所以,正確.

評析本題是中考數學填空題中多結論試題,綜合考查了與圓有關的知識,直角三角形內切圓的半徑公式,利用直角三角形的內切圓的圓心是內角平分線的交點,并作出輔助線構造全等三角形是解決本題的難點.靈活應用上述三個基本圖形的有關結論,對解決本題提供了幫助.

4 結語

著名數學家波利亞曾經說過:“解題的成功,要靠正確的轉化.”在教學中,特別是在復雜的幾何圖形分析的過程中,幫助學生從典型題目中總結提煉出基本圖形,學會從復雜的幾何圖形中拆分出基本圖形,或者需要添加輔助線來解決問題時,構造基本圖形能快速地解決問題,同時培養學生的識圖能力和邏輯推理能力.