“十字”模型及其應(yīng)用

江蘇省南京市板橋中學(xué)(210039) 紀(jì)明亮

幾何是初中數(shù)學(xué)的重點(diǎn)和難點(diǎn),有的時候?yàn)橐坏缼缀晤}苦思冥想很久還是無法解答,有時為一道幾何題能巧妙的作出一種輔助線使問題解決而感到欣喜若狂,那么幾何題究竟為何這樣難以駕馭? 其實(shí)幾何題看似變幻莫測,但每道題都是有章可循的,可從中抽象出基本模型,抓住基本模型就可以抓住幾何題的本質(zhì),方能以不變應(yīng)萬變,“十字”模型就是一類重要的幾何模型,但此種幾何模型的研究并不多,本文對“十字”模型做了一些思考和研究,并將思考和研究的結(jié)果與大家分享.

1 模型分析

(1)正方形中“十字”模型1

如圖1, 在正方形ABCD中,E、F、G、H分別為AB、CD、BC、AD上的點(diǎn), 若EF⊥GH于點(diǎn)O, 結(jié)論:EF=GH.

證明: 如圖1, 過點(diǎn)E、G分別作EN⊥CD、GM⊥AD于N、M, 則∠ENF= ∠GMH= 90°,EN⊥GM于點(diǎn)P,EN=GM則∠EPG= 90°.由EF⊥GH于點(diǎn)O, 則∠EOG= 90°.由∠EPG+∠NEF= ∠MGH+∠EOG,則∠NEF= ∠MGH, 故ΔEFN∽= ΔGHM(ASA), 則EF=GH.

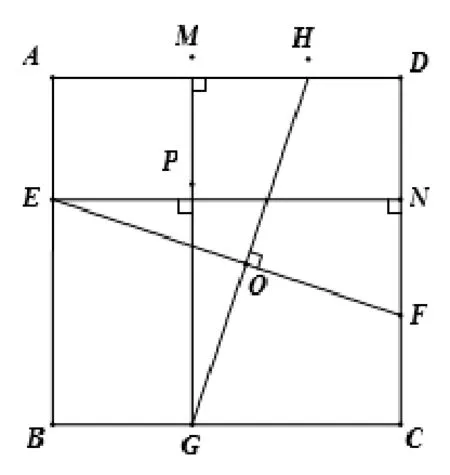
圖1

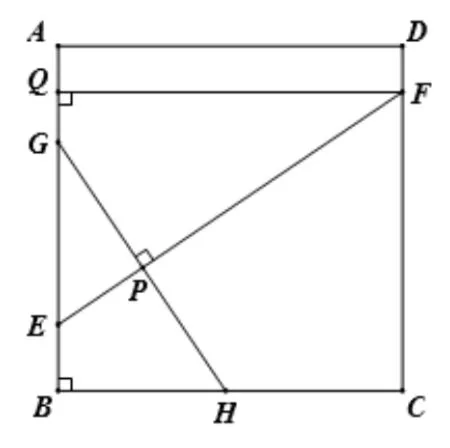
圖2

(2)正方形中“十字”模型2

如圖2, 在正方形ABCD中,E、F、G、H分別為AB、CD、AB、BC上的點(diǎn), 若EF⊥GH于點(diǎn)P, 結(jié)論:

證明: 過點(diǎn)F作FQ⊥AB于Q, 則∠EQF= 90°, 則∠EQF= ∠B, 由EF⊥GH于點(diǎn)P, 則∠GPE= 90°, 則∠GPE= ∠B, ∠QEF+ ∠EGP= ∠BHG+ ∠EGP則∠QEF= ∠BHG, 故ΔQEF∽ΔBHG, 則即

(3)矩形中“十字”模型

如圖3, 在長方形ABCD中,E、F、G、H分別為AB、CD、BC、AD上的點(diǎn), 若EF⊥GH于點(diǎn)O, 結(jié)論:

證明: 如圖3, 過點(diǎn)E、G分別作EN⊥CD、GM⊥AD于N、M,則∠ENF= ∠GMH= 90°,EN⊥GM于點(diǎn)P,則∠EPG= 90°, 由EF⊥GH于點(diǎn)O, 則∠EOG= 90°,由∠EPG+ ∠NEF= ∠MGH+ ∠EOG, 則∠NEF=∠MGH,故ΔEFN∽ΔGHM,則

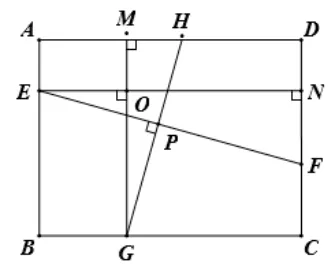
圖3

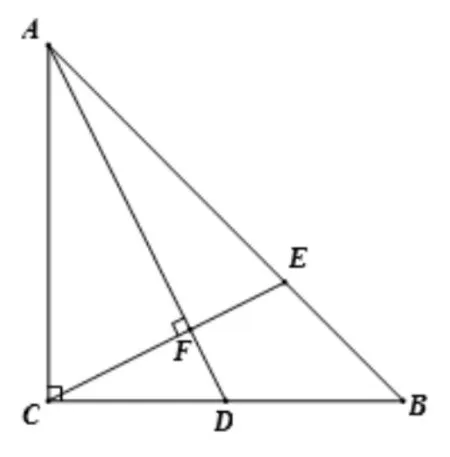
圖4

“十字”模型是以線段“垂直”為基礎(chǔ),在正方形、矩形里構(gòu)建直角三角形,再借助“垂直”關(guān)系證明所構(gòu)建的直角三角形全等或相似得到相應(yīng)的邊之間的數(shù)量關(guān)系,這是對“垂直”這一條件作用的升華,使其在解題中發(fā)揮更大作用.那么什么題目符合“十字”模型?“十字”模型在解題中的關(guān)鍵作用是什么? 下面通過幾道題目回答這兩個問題.

2 模型應(yīng)用

題1如圖4, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC= 4, 點(diǎn)D是BC中點(diǎn),CE⊥AD于點(diǎn)F, 交AB于點(diǎn)E,求CE的長.

分析: 因?yàn)镃E⊥AD于點(diǎn)F,且ΔABC是等腰直角三角形,這是正方形中的“十字”模型1,可根據(jù)此模型作輔助線構(gòu)建圖形解題.

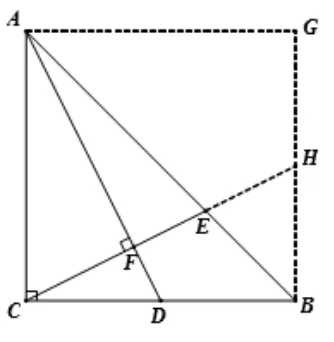
圖5

解如圖5, 以CA、CB為鄰邊構(gòu)造正方形ACBG,延長CE交BG于點(diǎn)H.由四邊形ACBG是正方形,則∠ACD= ∠CBH= 90°,AC//BG,由BC=4,點(diǎn)D是BC中點(diǎn), 則CD= 2.在RtΔACD中根據(jù)勾股定理, 可得AD=由CE⊥AD于點(diǎn)F,則∠AFD= 90°,則∠CAD+∠ACF=90°, 由∠ACF+ ∠BCH= 90°, 則∠CAD= ∠BCH,再 由AC=CB, 故RtΔACD∽= RtΔCBH(ASA), 則CH=AD=BH=CD= 2(“十字”模型) .由AC//BG,故ΔACE∽ΔBHE,則則即CE=

點(diǎn)評: 幾何計(jì)算一般采用勾股定理(建方程)、三角形相似、三角函數(shù)、等積法等方法, 而題中CE不在直角三角形中,則不能直接用勾股定理和三角函數(shù)求解,其所在三角形在原圖中也很難找到與之相似的三角形,等積法也很難行得通,這就需要作輔助線,那么輔助線如何作? 這里“CE⊥AD于點(diǎn)F,且ΔABC是等腰直角三角形”就是突破口,這是正方形中“十字”模型1 的典型特征,由此引領(lǐng)本題如何作輔助線構(gòu)建圖形解題.

變式1如圖6, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC= 4, 點(diǎn)D、M分別是BC、AC上的點(diǎn), 且滿足BD=CM= 1,CE⊥DM于點(diǎn)F,交AB于點(diǎn)E,求CE的長.

分析: 因?yàn)椤癈E⊥DM于點(diǎn)F,且ΔABC是等腰直角三角形,點(diǎn)D、M分別是BC、AC上的點(diǎn)”,這是正方形中的“十字”模型2,可根據(jù)此模型構(gòu)建圖形解題.

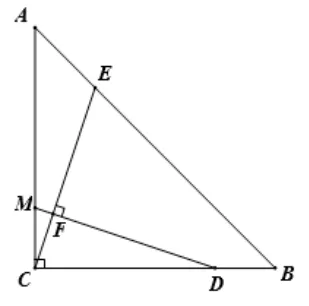
圖6

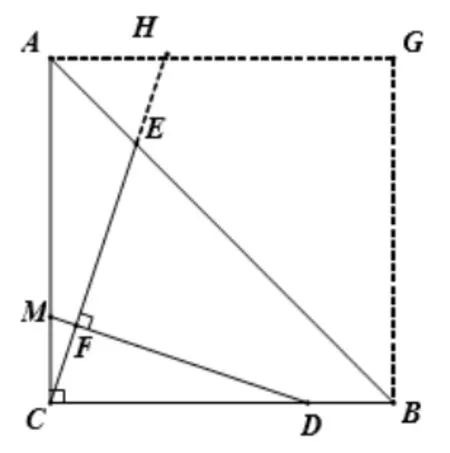
圖7

解如圖7, 以CA、CB為鄰邊構(gòu)造正方形ACBG,并延長CE交BG于點(diǎn)H.由四邊形ACBG是正方形, 則∠ACB= ∠CAG= 90°,BC//AG, 由BC= 4,BD= 1, 則CD= 3, 在RtΔCDM中 根 據(jù) 勾 股定 理得DM=由CE⊥DM于點(diǎn)F, 則∠CFD= 90°, 則∠CDF+ ∠FCD= 90°, 并由∠FCD+ ∠ACH= 90°, 可得∠ACH= ∠CDF, 故ΔACH∽ΔCDM, 則可 得CH=由BC//AG,故ΔBEC∽ ΔAEH, 則= 3, 則

點(diǎn)評: 本題情況和題1 類似,CE的長度很難求出,需要作輔助線,構(gòu)建圖形.同樣這里“CE⊥AD于點(diǎn)F,且ΔABC是等腰直角三角形”,顯然這是正方形中“十字”模型,通過構(gòu)造出正方形,發(fā)現(xiàn)這是正方形中的“十字”模型2,根據(jù)這個模型,將所求線段化歸到三角形中利用相似關(guān)系求出.

變式2如圖6, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC=4,點(diǎn)D在BC上的點(diǎn)(不與點(diǎn)B、C重合),點(diǎn)M在AC邊上,滿足BD=CM,CE⊥DM于點(diǎn)F,交AB于點(diǎn)E,求的值.

分析: 因?yàn)镃E⊥DM于點(diǎn)F,且ΔABC是等腰直角三角形,這是正方形中的“十字”模型2,可根據(jù)此模型構(gòu)圖解題.

解如圖7, 以CA、CB為鄰邊構(gòu)造正方形ACBG,延長CE交BG于點(diǎn)H.由四邊形ACBG是正方形, 則∠ACB= ∠CAG= 90°,且BC//AG.設(shè)BD=CM=x,由BC= 4,則CD= 4?x,在RtΔCDM中根據(jù)勾股定理得DM=由CE⊥DM于點(diǎn)F,則∠CFD= 90°,則∠CDF+∠FCD= 90°,再由∠FCD+∠ACH=90°,則∠ACH=∠CDF,故ΔACH∽ΔCDM, 則即則CH=由BC//AG, 故ΔBEC∽ ΔAEH, 則即, 則CE=

點(diǎn)評: 本題是變式1 當(dāng)中問題的一般化,D、M都是動點(diǎn),但任滿足BD=CM,從變式1 可以發(fā)現(xiàn)CE=DM,那么本題中關(guān)鍵就是求出CE、DM的數(shù)量關(guān)系,如果僅從原有圖形思考很難有所進(jìn)展,顯然要作輔助線構(gòu)圖,這與變式1的模型相同,也是正方形中的“十字”模型2,可根據(jù)此模型構(gòu)建圖形,由于D、M都是動點(diǎn),可設(shè)BD=CM=x,便于求出CE、DM的數(shù)量關(guān)系,解決問題.

變式3如圖8,在ΔABC中,AB=AC,∠ABC=60°,點(diǎn)D在AB邊上(不與點(diǎn)A、B重合),點(diǎn)E在AC邊上,滿足CE=AD,過點(diǎn)A作AH⊥DE于點(diǎn)F,交BC于點(diǎn)H,求值.

分析: 因?yàn)椤包c(diǎn)D在AB邊上(不與點(diǎn)A、B重合),點(diǎn)E在AC邊上AH⊥DE于點(diǎn)F,且ΔABC是等邊三角形,”,這是矩形中“十字”模型,可根據(jù)此模型將問題劃歸到矩形中借助矩形中“十字”模型來解決問題.

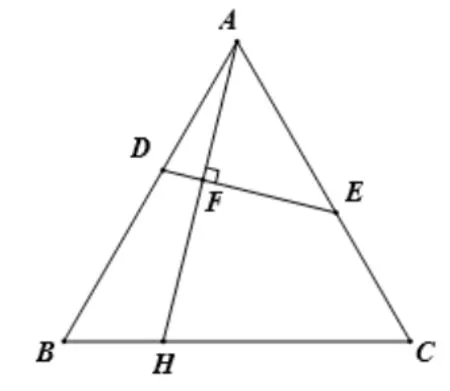
圖8

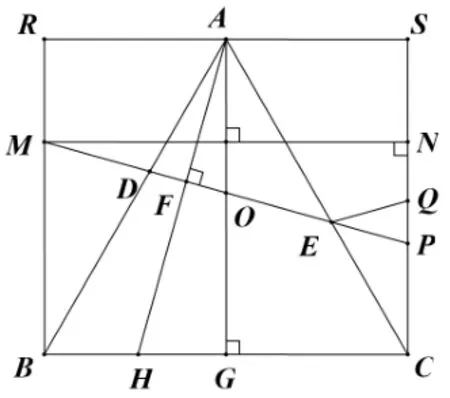
圖9

解如圖9, 以BC為邊, 點(diǎn)A對邊上一點(diǎn)構(gòu)造矩形BCSR, 延長DE交BE、CR于M、P, 過點(diǎn)M, 作MN⊥CS于點(diǎn)N, 在CS上取點(diǎn)Q, 使EP=EQ, 過點(diǎn)A作AG⊥BC于點(diǎn)G.由于AG⊥BC于點(diǎn)G, 則AG⊥MN, 則∠OMN= ∠OAF, 由于MN⊥CS于點(diǎn)N,則∠MNP= 90°, 則∠MNP= ∠AGH, 則ΔMNP∽ΔAGH, 則由AG//CS, 則∠AOD= ∠EPQ.由EP=EQ,則∠EPQ= ∠EQP,則∠AOD= ∠EQP.由∠DAO= ∠ECQ= 30°,AD=CE,故ΔDAO∽= ΔECQ(AAS),則OD=EQ,則OD=EP.由OM=OP,則OD+MD=OE+EP,即MD=OE,則MD+EP=OD+OE, 則DE=

點(diǎn)評: 本題和變式2 類似,也是動點(diǎn)問題中求邊的比值,直接求非常困難, 因此要依托于圖形, 而點(diǎn)D在AB邊上(不與點(diǎn)A、B重合),點(diǎn)E在AC邊上AH⊥DE于點(diǎn)F,且ΔABC是等邊三角形,這是矩形中“十字”模型,則根據(jù)此模型構(gòu)造出矩形和直角三角形,再根據(jù)圖形關(guān)系求出值.

3 結(jié)語

在解題中模型的作用實(shí)際上是解題思路的引領(lǐng),每一種模型都可以推導(dǎo)出確定的結(jié)果,借助模型能更好的發(fā)現(xiàn)題目中的規(guī)律, 能透過現(xiàn)象看本質(zhì).在幾何問題中有的條件(圖形)給的非常隱晦,很難明白其用意,不知如何轉(zhuǎn)化,那么問題就難以解決,像以上四道題,每道題都給了“垂直”,而“垂直”是“十字”模型的必要條件,這樣可以試用“十字”模型構(gòu)建圖形,通過“十字”模型引領(lǐng)輔助線作法,巧妙構(gòu)圖,化難為易,將四道題都解決了.