常量替換再探究
——一節研究性學習課的教學實錄與反思

廣東省廣州市番禺中學(511400) 黃 殷

《數學通報》2011 年第10 期第30 頁刊登了李愛生老師的《常數替換 精彩迭現》[1]一文,筆者讀后受益匪淺.該文從一道例題出發,利用“常量替換法”探究出圓錐曲線的多個結論.筆者認為該文章里的一些定理,還值得作進一步的探究推廣,于是挑選了其中的定理7、8、9,在學校高二數學研究性學習課堂里,進行了探究教學,取得了不錯的效果.以下是本節課的課堂實錄與反思.

1 原問題呈現

定理7P(s,t)是橢圓=1(a ＞0,b ＞0)上一點,直線l與該橢圓相交于A、B兩點,且PA⊥PB,則直線l過定點

定理8P(s,t)是雙曲線=1(a ＞0,b ＞0,a/=b)上一點,直線l與該雙曲線相交于A、B兩點,且PA⊥PB,則直線l過定點

定理9P(s,t)是拋物線y2=2px(p/=0)上一點,直線l與該拋物線相交于A、B兩點,且PA⊥PB,則直線l過定點(s+2p,?t).

對于定理8,筆者在黑板上展示了李老師給出的證明過程:

設A(x1,y1),B(x2,y2), 直 線l:y=kx+m, 即雙曲線即

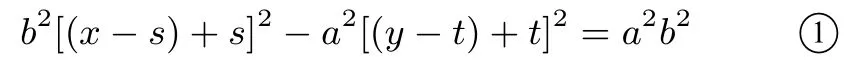
又因P(s,t) 在雙曲線上, 故有= 1, 即b2s2?a2t2=a2b2, 所 以①可化為b2(x ?s)2?a2(y ?t)2+2[b2(x ?s)s ?a2(y ?t)t]·1=0,即

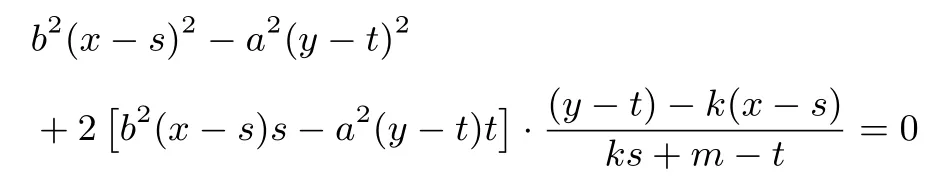
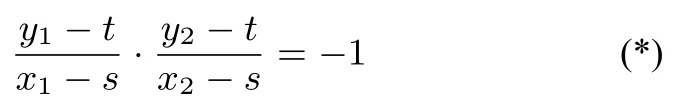
得:=?1, 即m=故直線l的方程為該直線經過定點當直線的斜率不存在時,驗算可知,結論仍成立.

2 教師引導探究

在展示了以上證明過程后,筆者提出了以下問題,引導學生進行探究.

欣賞了剛才的推導過程, 學生聽到老師所提的問題后,均躍躍欲試,在做一番推導和討論交流后,有一位學生舉起了手,我讓他上臺板書.

師: 很好! 參考剛才這位同學推導的結論,我們是不是可得到以下精彩的結論呢?

結論1P(s,t) 是雙曲線= 1(a ＞0,b ＞0) 上 一 點, 直線l與 該 雙 曲線相交 于A、B兩 點, 且kP A · kP B=n,n為常數且n /=則直線l過定點

學生紛紛點頭表示認同.看著自己推導出來的結論,學生的成功感油然而生!

師: 結論1 其實是定理8 的一般形式.對于定理7,我們能不能也得出它的一般形式呢?

學生異口同聲地回答: 能!

師: 怎樣得到呢?

師: 不錯! 這是一種常規的思路,但過程會繁瑣一些.大家再想想,有沒有其他的方法呢?

生3: 其實只要把雙曲線方程中的“?b2”改為“b2”, 就變成橢圓的方程了.那我覺得把結論1 中所有的“?b2”改為“b2”就行了.

生3 話音剛落,課室里發出了一陣討論聲,不少學生都在點頭,并向生3 投去敬佩的眼光.

師: 很好! 看來生3 這位同學確實是動了腦筋思考的.不錯, 剛才我們用“=n”替換了(*) 式的=?1”,得到了一個精彩的結論,現如果用“?b2”替換結論1 中的“b2”,我們同樣可以得到另一個精彩的結論.

結論2P(s,t) 是橢圓= 1(a ＞0,b ＞0)上一點, 直線l與該橢圓相交于A、B兩點, 且kP A ·kP B=n,n為常數且n /=則直線l過定點

這時,筆者明顯感覺到課室的“溫度”上升了,有在討論推導過程的, 也有在嘖嘖贊嘆的, 還聽到有學生討論定理9的一般形式.

師: 大家再想一想,能否進一步得出定理9 的一般形式呢?

幾個學生不約而同地說: 可以用“kP A ·kP B=n”代替定理9 中的“PA⊥PB”.

師: 非常好! 看來同學們已經感受到“替代”的威力了.下面給大家一點時間推導,然后請一位同學上臺來為大家板演.

生4: 證明: 設A(x1,y1),B(x2,y2),直線l:y=kx+m,即拋物線y2=2px可變為拋物線

又因P(s,t) 在拋物線y2= 2px上, 故有t2= 2ps, 所以②可 化 為(y ?t)2+ 2[t(y ?t)?p(x ?s)]·1 = 0, 即(y ?t)2+2[t(y ?t)?p(x ?s)]·整理,得因 為kP A · kP B=n, 所 以=n, 則=n,解得m=

故直線l的方程為y=?t,該直線經過定點當直線的斜率不存在時,驗算可知,結論仍成立.

師: 通過推導探究,我們不難發現,通過“替代”,在拋物線中也可以得到精彩的結論.

結論3P(s,t)是拋物線y2=2px(p/=0)上一點,直線l與該拋物線相交于A、B兩點,且kP A·kP B=n,n為常數且n/=0,則直線l過定點

3 層層推進,拓展探究

話音剛落,課室中開始“騷動”起來,討論聲、爭辯聲時起彼伏.

師(微笑,投去肯定的眼光): 你們可以大膽地試一試.

這兩位同學分別就雙曲線與橢圓、拋物線進行探究并上臺板書.

師: 根據同學們的推導,我們可得到以下一組更精彩的結論:

結論4P(s,t)是雙曲線上一點,直線l與該雙曲線相交于A、B兩點,且kP A+kP B=n,n為常數且n/=0,則直線l過定點

結論5P(s,t)是橢圓=1(a ＞0,b ＞0)上一點,直線l與該橢圓相交于A、B兩點,且kP A+kP B=n,n為常數且n/=0,則直線l過定點

結論6P(s,t)是拋物線y2= 2px上一點,直線l與該拋物線相交于A、B兩點, 且kP A+kP B=n,n為常數且n/=0,則直線l過定點

至此,學生們都雀躍地沉浸在自己探究所得的這些結論中.

師: 從一個問題出發,結合其產生的背景,通過探究推理,展望其未來的發展,這過程雖艱辛,但卻是快樂的! 只要我們抱著一顆不斷探索、不斷追求的恒心,其收獲一定是豐富而精彩的!

4 課后反思

4.1 關于數學研究性學習

數學研究性學習是一種實踐性較強的教育教學活動,學生應通過自己親身參與的探究活動來獲取知識、得出結論,而不是由教師將現成的知識、結論通過傳遞式教學直接教給學生.數學研究性學習所探究的問題不一定是課本上的,亦可充分利用課外的資源.除此,教師還要了解學生已有知識,學生能達到“最近發展區”等.本節研究性學習課就是在學生學習完“圓錐曲線”這一章,掌握了橢圓、雙曲線、拋物線的方程、圖像和性質等問題后開展的.

4.2 教師主導地位與學生的主體地位

新課程標準強調教學過程中學生的主體地位,因此教師要發揚民主教學,要鼓勵學生積極參與探究.更重要的是,教師應注意鼓勵學生提出獨立見解,還應認真聆聽學生的提問,引導學生從不同角度思考和探究問題,使學生的思維和創造性在課堂中發光.如本節課中學生2 的證明方法雖然比較麻煩,但卻是很多學生首先會想到的方法.教師此時就要發揮主導作用,一方面要給予充分的肯定,另一方面要引導學生思考其他的方法,喚醒學生的探究意識.

4.3 教師的設問是關鍵

本節課設置了一些列的啟發性問題, 如:“...改為...”、“能不能得出它的一般形式”、“有沒有其他的方法”這些問題都具有很大的發散性,從而激發了學生的求知欲望和創新熱情.學生通過參與探究過程,培養了自身的發散思維能力和創造性、開拓性思維品質.學生也能很好地感受到由探究所得帶來的成功感和喜悅感.