案例教學在自回歸模型教學中的應用

凌 云

（成都文理學院 四川·成都 610401）

0 前言

時間序列分析是統計學專業學生必修課程之一，在諸多領域都有著廣泛的應用。自回歸模型是時間序列分析的經典模型之一，強調其在實際中的應用，并將應用案例引入到日常教學中，將比較枯燥的數學模型與實踐緊密結合，不但能加強學生對自回歸模型的理解，豐富教學內容，擴大課堂信息量，而且能激發學生探索與學習的興趣，提升學生的專業能力。本文通過自回歸模型在人口預測中的應用，對案例教學在時間序列分析中的應用進行了粗略的探討。

1 重要概念

構建AR(p)模型的步驟：

步驟1：對序列作平穩性檢驗，若經檢驗判定為非平穩，用平穩化方法將序列作平穩化處理；

步驟2：對平穩的序列作白噪聲檢驗，若經檢驗判定序列為白噪聲，建模結束；否則，轉步驟3；

步驟3：對模型進行識別，估計其參數，轉步驟4；

步驟4：檢驗模型的實用型，若估計的參數通過檢驗，殘差為白噪聲，則得到擬合模型并可以對序列作預測；否則轉步驟3。

在步驟1中，判斷一個時間序列是否平穩的最簡單也是最直觀的方法就是時序圖法。將一個時間序列按時間順序繪成連線圖，若其始終在一個常數值上下隨機波動，波動強度隨時間變化不大，沒有明顯的趨勢性和周期性，則認為該序列是平穩的。若序列不平穩，常用的平穩化方法有差分、趨勢擬合、移動平均和指數平滑。

在步驟3中，通過自相關系數、偏自相關系數的截尾性與拖尾性作為模型識別的依據。若自相關系數拖尾，偏自相關系數p階截尾，則可建立AR(p)模型。需要注意的是，如果識別出的不只一個模型，則需要根據AIC等準則來進行比較并選出最合適的模型。

在步驟4中，殘差為白噪聲是判斷模型有效性的標準之一。時間序列分析的目的之一就是要將序列中的相關信息充分提取出來，一旦被充分提取，那么剩余的殘差序列就應該是白噪聲序列。

筆者在進行自回歸模型的教學中發現，僅從理論的角度進行講解，并不能引起學生的興趣，同時使得學生難以用于實際問題中，不利于培養學生的專業能力。針對這個問題，結合自回歸模型的廣泛應用案例，在理論概念講解之后，將其運用于實際問題——人口預測中，引導學生探索問題—收集數據—建立模型—預測，同時通過Eviews軟件上機操作，加深學生對這部分知識的理解，培養學生的專業技能，提高教學效果。

2 案例分析

人口問題依然是目前世界普遍關心的重大問題之一。中國總人口數是指中國在某一時間點上的人口總數，人口眾多、人均資源少依然是我國的基本國情，人口與經濟、社會、資源和環境等各方面的不夠協調仍是我國目前發展面臨的重要問題之一。因而，利用數據探究我國人口總數的變化趨勢、預測人口總量的變化，對與民生政策、經濟政策、人與自然的和諧發展具有重要意義。本文根據上述理論，對1952-2018年中國總人口數序列進行分析。

2.1 中國總人口數序列的平穩性分析

對給定的時間序列，在建模時，序列應滿足平穩性，故對1952-2018年中國總人口數序列作時序圖進行觀察，以此獲得序列值的趨勢和走向以及不同時刻序列值之間的相關關系。其時序圖如下圖1：

圖1：1952-2018年中國總人口數時序圖

由時序圖可以得出，1952-2018年中國總人口數序列是非平穩的。于是，我們需要對該序列作平穩化處理。

1952-2018年中國總人口數序列有明顯的線性增長趨勢。因此可以考慮對該序列作一階差分：

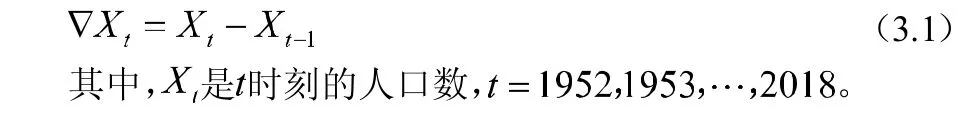
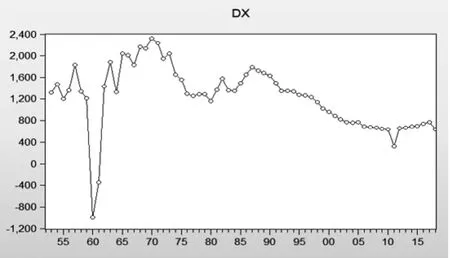
圖2：1952-2018年中國總人口數一階差分后的序列時序圖

由時序圖，該序列沒有明顯的趨勢與周期，可以認為該序列是平穩的。

2.2 中國總人口數一階差分后的序列的純隨機性檢驗

對給定的時間序列，在建模時，序列除了滿足平穩性，還需要滿足非白噪聲。故對中國總人口數一階差分后的序列作純隨機性檢驗，見圖3。

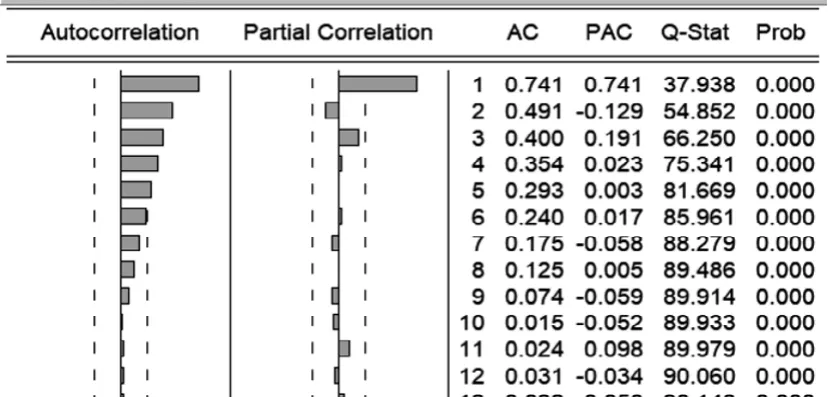
圖3：一階差分后的序列的純隨機性檢驗結果

由圖3可知，在任意滯后階數下，該序列的Q統計量檢驗的伴隨概率均顯著為0，因此拒絕其是純隨機序列的假設，可以認為該序列不是隨機序列，滿足序列是非白噪聲的要求。可以對該序列建立時間序列模型。

2.3 構建模型

通過觀察圖3中的自相關系數、偏自相關系數，可以得出該序列的自相關系數拖尾，偏自相關系數1階截尾，因此可以建立AR(1)模型。

圖 4：AR（1）擬合相關參數圖

構建的模型結果如下：

結果顯示，AR(1)的p值小于0.05，通過了顯著性檢驗。

通過殘差序列進一步對模型的有效性作檢驗：

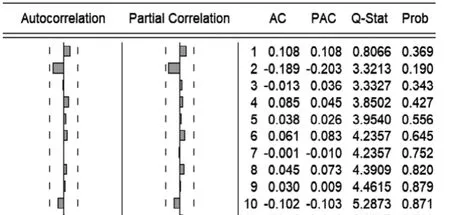
圖5：AR（1）擬合殘差的純隨機性檢驗結果

由圖5可得，殘差序列全部在二倍標準差的范圍中，顯示出良好的擬合效果。最后建立AR（1）模型如下：

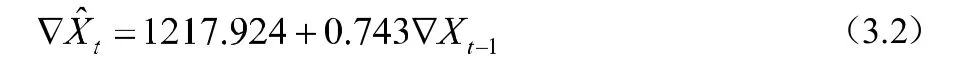
根據（3.1）與（3.2）建立我國1952-2018年總人口數的組合模型：

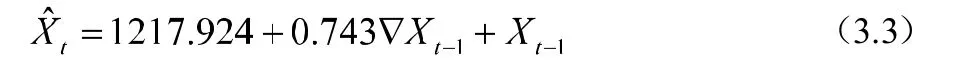
該組合模型的擬合效果是比較好的，見圖6。

圖6：組合模型的真實值x與擬合值DF的擬合效果

2.4 基于構建模型的人口預測

根據（3.3）式對2019年我國人口總數進行預測，預測值為140961.986萬人。2019年我國人口總數的真實值為139772萬人，真實值與預測值的相對誤差為0.85%。該模型的預測效果是比較好的。

3 總結

自回歸模型是時間序列分析的重要教學內容之一，其概念、性質和建模流程相對比較枯燥，教師僅從理論部分進行講解，學生會難以與實際問題相聯系。引入人口預測案例，通過Eviews軟件上機實踐，用完整的實際問題建模，能夠幫助學生理解自回歸模型的概念、應用及軟件實現，更好的達到學以致用的目的。當然，自回歸模型在實際中的的應用非常廣泛，可引用的教學案例較多。例如，旅游人數預測問題、國內生產總值預測問題、氣溫預測問題等等。教師在教學過程中，可以選擇更貼近學生學習基礎，更能引起學生的興趣的案例。同時，教師在將自回歸模型用于人口預測中，可引導學生自主建模，完成探索問題—收集數據—建立模型—預測以及利用Eviews軟件實現建模的過程，培養學生的專業能力。