淺析Matlab在線性代數教學中的應用

陳朝敏

（陸軍步兵學院 江西·南昌 330100）

0 引言

線性代數是高等院校理工專業學生必修的一門重要的數學課程，其主要的數學工具，即矩陣理論，在眾多領域都有應用。同時，線性代數也是學習其他課程的基礎課程。近十幾年來，隨著我國信息化的不斷深入，線性代數應用的廣度和深度都有很大的提升，在這個大背景下，給線性代數的教學提出了更高的任務和要求，如何使學生在現有學時較少的條件下不僅掌握線性代數的系統知識，還能著重培養學生的代數思維和應用能力，成為新的教學研究方向。

線性代數具有基礎概念多、理論邏輯性強、計算過程較繁瑣等特點，但當前線性代數教學沒有很好的平衡系統知識教學與案例式教學之間的關系，一是偏重于從數學問題到數學問題的解，教學實例較少，脫離實際應用背景；二是教學中涉及到的計算方法，如行列式計算、可逆矩陣求逆矩陣、求矩陣特征值和特征向量等，在低階情況下，學生尚能接受，但對于高階情況，手動計算顯得較為困難，這導致線性代數較難應用于涉及高階和復矩陣問題的后續課程，后果就是產生“數學無用論”的錯誤觀點，無法提升學習的內動力，基于此研究現狀，提出將Matlab應用于線性代數教學，論證對破解當前教學障礙、提升教學效果的可行性。

1 Matlab應用于線性代數教學的可行性

Matlab的產生與發展與計算機密不可分。1980年，美國計算機教授Cleve Moler在講授線性代數時，為解決學生在高級語言編程上的難題，編寫了Fortran子程序庫接口程序，并命名為Matlab（取MatrixLabroary前三個字母，即矩陣實驗室）。Matlab這一強大的科學計算軟件越來越受到高校師生和廣大科研人員的認可，在國內，部分高校也開設了Matlab相關課程。基于 Matlab強大的科學計算能力和圖形處理功能，可以簡化線性代數中涉及的復雜計算，對難以理解的概念通過可視化的方式加深理解，對線性代數的理解從感性認識提升到理性認識，培塑學生理論結合實際的素養，激發學習內動力。

2 Matlab應用于線性代數教學應注意的問題

Matlab應用于線性代數教學的益處不再贅述，但在運用中，需要考慮以下幾個方面的問題：

（1）教學重點不能偏移。線性代數的“三個基本”仍是教學重點，只有掌握了系統全面的理論知識，才能更好的理解代數思維，Matlab只是輔助教學工具，不能將線性代數教學變成數學軟件學習。

（2）適當補充必要的基礎知識。Matlab的運用不止在第一課堂教學，更重要的是讓學生在第二課堂利用Matlab解決學習中遇到的困難，所以應適當補充必要的軟件基礎知識，包括推薦整理Matlab學習資料給學有余力的學生，為接下來的數學建模競賽打下良好的數學軟件基礎。

（3）針對學生的個體差異性設置不同難度的數學實驗，Matlab應用于線性代數教學的最終目的是訓練學生的代數思維與實操能力。因此，可根據學生的個體差異性設置不用難度的數學實驗，并要求學生撰寫實驗報告，以檢驗教學效果。

3 Matlab應用于線性代數教學的具體探討

在研究了線性代數課程地位、特點、教學現狀、Matlab應用于線性代數教學的可行性和需要注意的問題后，就降低計算復雜度、顯化概念理解、提升應用能力三個方面展開Matlab應用于線性代數教學的具體探討。

3.1 功能強大的eig函數

矩陣特征值和特征向量在很多工程問題都有應用。根據特征值和特征向量的定義和性質，求矩陣A特征值和特征向量的方法如下：

因此，通過手工計算求高階方陣的特征值和特征向量顯得十分困難。正確的做法是在低階情形下研究特征值和特征向量的性質，在此基礎上，運用Matlab強大的數值計算能力簡化高階情形下的特征值和特征向量的求解。

Matlab提供了一個求矩陣特征值和特征向量的函數eig，其具體用法見下表1。

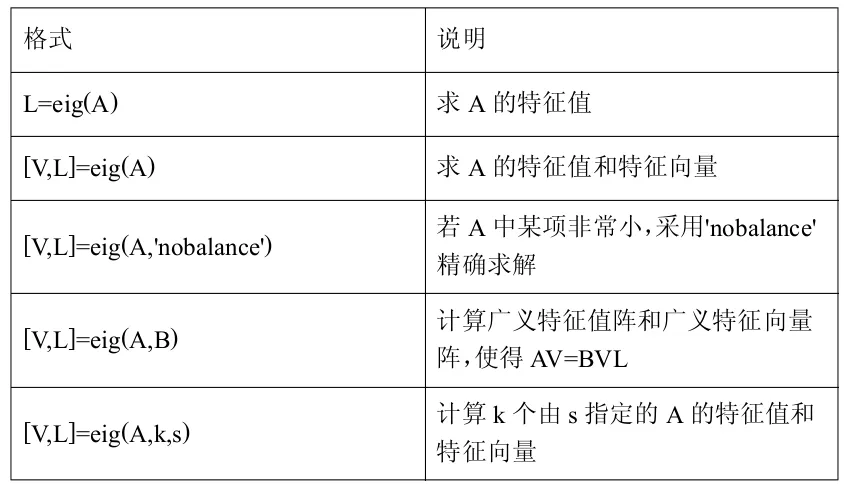
表1：eig函數的用法

3.2 可視化的力量

當前，教材中通常是利用坐標旋轉變換介紹二次型這一知識點，這種從代數角度去理解二次型較為抽象，利用Matlab強大的可視化功能，采用數形結合的方法，將二次型以圖形演示的方式展現出來，顯化抽象概念，提升教學效果。

得到圖形，如圖1所示。

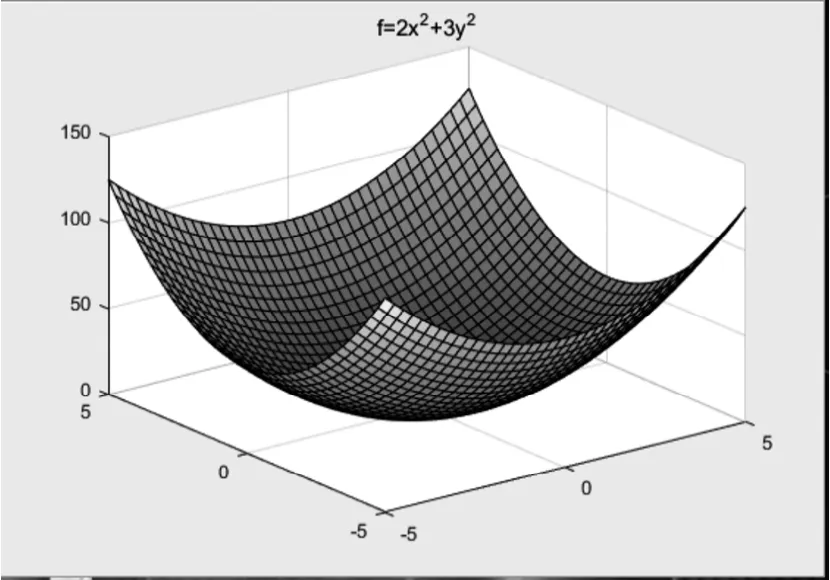
圖1：正定二次型

由圖1可知，正定二次型的圖形都位于xoy平面上方。

3.3 矩陣運算的妙處

Leonado Fibonacci在其提出的兔子問題中引出斐波那契數列。與斐波那契數列有關的應用還包括著名的楊輝三角、黃金數等，那么該如何求出斐波那契數列的通項呢？

這里采用矩陣理論來研究斐波那契數列。

由斐波那契數列的定義和性質可得到如下差分方程組：

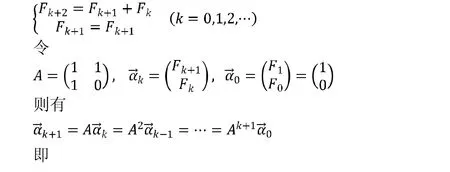
相比于運用矩陣對角化來求解要簡便快捷，更能凸顯線性代數的應用價值。

4 總結

本文主要就如何提升線性代數教學效果進行了研究，提出了將Matlab應用于線性代數教學的觀點，并剖析了在具體運用實施時應注意的幾個問題，最后就降低計算復雜度、顯化概念理解、提升應用能力三個方面展開Matlab應用于線性代數教學的探討。