充分發揮導學作用　構建高效數學課堂

邱言貴

[摘 要]數學課堂中，教師要充分發揮自身的引導作用，使學生學會分析類比、好中選優、修正錯誤、獨立思考，促進學生數學思維的發展，實現“不同的人在數學學習上得到不同發展”的目的，真正構建高效課堂。

[關鍵詞]導學;數學課堂;類比;錯誤;思考

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）06-0028-02

真正高效的數學課堂，每一位學生都全身心地投入其中。要做到這一點，教師就要充分發揮自身的導學作用，引導學生動手、動口、動腦，發展學生的數學思維，使學生真正習得數學知識。

一、聯系知識，分析類比

數學學習的目的在于理解和掌握數學知識，然后在此基礎上通過分析類比，體會數學知識與方法之間的聯系。通過分析類比，學生可進一步整理和歸納所學的數學知識與方法;反之，能夠深化學生對所學數學知識與方法的理解。

多媒體出示題目1：東街小學師生35人，帶土筐40只，幫助工地運土。教師每人挑2只土筐，學生兩人抬1只土筐。那么，教師和學生各有多少人？

師：我們以前有沒有見過類似的題目？對于類似的題目，我們是怎么解決的？

生1：這道題目感覺并不陌生。

師：如果我們把題中的人換成動物呢？

生2：這道題類似我們學過的“雞兔同籠”問題。

師：讓我們一起來復習“雞兔同籠”問題。（多媒體出示題目2，如下）我們通常用什么方法來解題的？

題目2：已知籠里有若干只雞和兔。從上面數有35個頭，從下面數有94只腳。那么，雞和兔各有多少只？

生3：我們一般用假設法來解答“雞兔同籠”問題。首先，假設全是雞，即根據雞和兔的總數，可以算出假設條件下一共有多少條腿;其次，把計算出來的腿數和題中的腿數相比較，看看相差多少，每差兩條腿就有一只兔，將所差的腿數除以2就可以知道共有多少只兔;最后，反過來求雞的只數。

師：這位同學的解題思路非常清晰，請同學們用假設法來解答題目1。

生4：假設35人都是教師，則一共需要2×35=70（只）土筐，實際上只有40只土筐，多出了70-40=30（只）土筐;教師一人用2只土筐，學生一人用1÷2=0.5（只）土筐，把一個學生當作教師，便多出了2-0.5=1.5（只）土筐，所以學生的人數是30÷1.5=20（人），教師的人數是35-20=15（人）。

師：這位同學的解答過程完全正確。

生5：看來，“雞兔同籠”問題不一定與雞和兔有關聯，還可能和別的動物以及人有關。這類問題真是多變啊！但是，我們可以用假設法來解決這類問題。

……

在學習過程中，學生會遇到各種各樣的新問題，將新問題和舊問題進行分析類比，找到相似之處，便可以用舊方法解決新問題。如上述教學，教師引導學生把題目和“雞兔同籠”問題進行類比，使學生能運用假設法解決問題，培養了學生的邏輯推理能力。

二、探求解法，好中選優

數學課堂中，為了培養學生的開放性思維，教師在新課導入和習題講解時會鼓勵學生探究同一問題的多種解法，也就是常說的一題多解。一題多解能夠給學生提供多種選擇，讓學生有更多的方法解決問題，但是學生要有能力選擇解決問題的最佳方法。因此，教師和學生要一起探究問題的多種解法，使學生學會好中選優，提高學生解決問題的能力。

多媒體出示題目：公立小學五年級共有學生270人，其中女生人數是男生人數的4/5，那么男、女生各有多少人？

生1：270×4/9=120（人），270×5/9=150（人）。

生2：270÷9=30（人），30×4=120（人），30×5=150（人）。

生3：270÷（1+4/5）=150（人），150×4/5=120（人）。

生4：270÷（1+5/4）=120（人），120÷4/5=150（人）。

師：請同學們想一想，這四種方法中的算式是怎么來的？一會兒，老師會依次請同學上來講述解題過程，然后同學們比較這四種方法，選擇一種自己喜歡的方法。如果有時間，我們還可以開展投票活動，選出大家公認的簡便解法。

……

上述教學，教師沒有直接對各種解法進行評價，而是讓學生比較后選擇自己喜歡的解法。因為同一道題目，不同的學生解題的角度不同;同一種算法，不同的學生給出的判斷也不同。那為什么還要開展好中選優這樣一個活動呢？一方面可讓學生接觸到多種多樣的解題方法，培養學生的發散性思維;另一方面能使學生找到最適合自己的解題方法，提高學生解決問題的能力。

三、反思錯題，修正錯誤

實踐證明，讓學生修正錯誤并不難，困難的是讓學生明晰錯誤的原因。因此，教師在教學中要盡可能地給予學生反思錯誤的時間，和學生一起找錯、糾錯，使學生真正理解與掌握所學的數學知識。

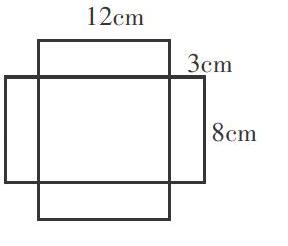
例如，有這一道數學題：“這是一個長方形紙盒的展開圖（如右），做這個紙盒需要多少材料呢？”看似一道比較簡單的計算題，學生卻出現了三種答案，只有一種答案是正確的。教師沒有直接否定錯誤的答案，而是讓學生分享自己的解題思路。

生1：這道題的問題是“做這個紙盒需要多少材料呢”，那么只需要計算出長方體的表面積即可。同時，這道題給出了長方體的長、寬、高，可以分別計算出每個面的面積后再相加，所以我求出的答案是312平方厘米。

師：這位同學的解題過程非常流暢！那你能畫出這個長方體的展開圖嗎？（生1畫圖，如右）

生2：這兩個展開圖并不一樣呀！

生1：我忽略了題中的圖形，只需要算出五個面的面積就夠了，而我多算了一個面的面積。

師：這位同學受思維定式影響，導致解題出現錯誤，所以同學們今后一定要注意審題。

生3：我覺得這個長方體紙盒前后兩個面和下面的面可以看作一個大長方形，左右兩個面看作兩個小長方形，所以我求出的答案是180平方厘米。

師：這位同學在計算長方體紙盒的表面積時，對圖形進行了調整，本來要算五個面的面積，調整后只需要算三個面的面積，對計算過程進行了簡化，老師非常欣賞這位同學。但是，老師也產生了一個問題，就是這個大長方形的長和寬分別是多少呢？

生3：這個大長方形的長是12厘米，寬是11厘米。

生4：不對！這個大長方形的長應該是8+3+3=14（厘米），寬是12厘米。

生3：哎呀，我在計算過程中漏算了，真是馬虎大意！

師：看來，這位同學是由于計算不仔細出錯的，真是讓人感到非常可惜呢！所以，同學們解題后要進行驗算，這樣可以提高計算的正確率。

……

上述教學，教師在幫助學生認識到自己錯誤的同時，挖掘了學生身上的閃光點，使學生更加喜歡上數學。有些心理比較敏感的學生非常害怕出錯，教師在教學中多進行這樣的溝通，能夠讓學生認識到出錯并不可怕。同時，教師對學生的提示和表揚，能夠幫助學生樹立學好數學的信心，使學生更加積極主動地探究數學。

四、引導觀察，促進思考

觀察能力是學生必須具備的一種能力，可以提高數學學習的效率和質量。因此，數學課堂中，教師要想方設法培養學生的觀察能力，引導學生多角度觀察，促進學生深入思考問題。

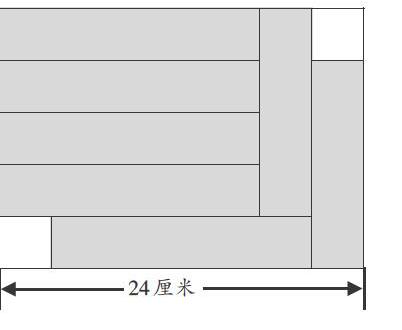
例如，有這樣一道組合圖形的“找規律”題（如右圖）：“7個完全相同的長方形拼成了圖中的陰影部分，圖中空白部分的面積是多少平方厘米？”面對這道題，很多學生都非常頭疼，不知道該如何分析解題。

師：首先，我們分析整個圖形。這個大長方形里有什么呢？

生1：這個大長方形總共有7個小長方形，且這7個小長方形相同。

師：那題目中給出的24厘米表示什么意思呢？同學們還能不能觀察到其他信息？

生2：我發現一個小長方形的長等于4個小長方形的寬。

師：這位同學觀察得很仔細，一下子找到了題目中一個非常關鍵的信息。

生3：我還發現24厘米等于一個小長方形的長加上兩個小長方形的寬，這樣就可以算出一個小長方形的寬是多少，即24÷6=4（厘米）。可是，空白部分的面積又該怎么計算呢？

生4：觀察圖形下面的空白部分，可以知道它的寬等于一個小長方形的寬，它的長等于總長24厘米減去一個小長方形的長和寬，而總長24厘米由6個小長方形的寬組成，減去4個小長方形的寬后，再減去一個小長方形的寬，還剩下一個小長方形的寬。所以，這個空白部分是一個正方形，這樣就可以計算出兩個空白部分的面積了。

師：看來，同學們的觀察能力還是比較強的。純數字類的規律題與圖形類的規律題相比更難，因為解答圖形類的規律題不僅要分析數字，還要分析不同圖形的組合。

……

上述教學，教師逐步引導學生分析組合圖形，即先分析組合圖形的構成，如“由幾個小圖形組成的”等，再找出題目中隱藏的數量關系，分析數字變化的規律，最后解決問題。這樣教學有效地培養了學生的數學思維，提高學生解決問題的能力。

總之，在數學課堂中，教師要充分發揮自身的引導作用，如引導學生分析類比、選擇解題方法等，使學生學習的數學能力和數學思維都能夠得到有效培養，在數學學習上獲得不同的發展，真正構建高效課堂。

（責編 杜 華）