單調(diào)變分不等式的改進次梯度外梯度算法

張雙德， 夏福全， 黃 瑕

（四川師范大學 數(shù)學科學學院，四川成都610066）

設H是Hilbert空間，其內(nèi)積和范數(shù)分別表示為〈·，·〉和‖·‖.變分不等式（VI）問題是求x*∈C，使得對?x∈C，都有

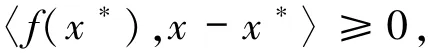
其中C是H中的一個非空閉凸子集，f：C→H是一個映射.變分不等式問題和它的解集分別用VI（C，f）和SOL（C，f）表示.變分不等式問題是優(yōu)化理論中的一個基本問題，同時在結構分析、工程科學、經(jīng)濟科學、運籌學、自動控制等領域也具有廣泛的應用［1-5］.

為了解決變分不等式問題，Korpelevich［1］提出Rn空間中的外梯度算法（EG）：

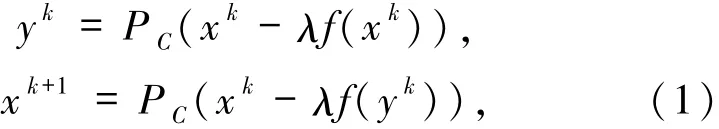
其中λ＞0，PC是H→C的投影.在f是單調(diào)和Lipschitz連續(xù)且Lipschitz系數(shù)為的條件下，證明了算法所生成的序列收斂到解集中的一點.

在上述外梯度算法（EG）的每次迭代過程中，需要計算兩次向C的投影，其中C是一個一般的非空閉凸集，這樣的投影不容易實現(xiàn).為了克服這個困難，Censor等［2］提出一種次梯度外梯度算法，該算法將（1）式中的投影換成向一個特殊結構的半空間Tk的投影：

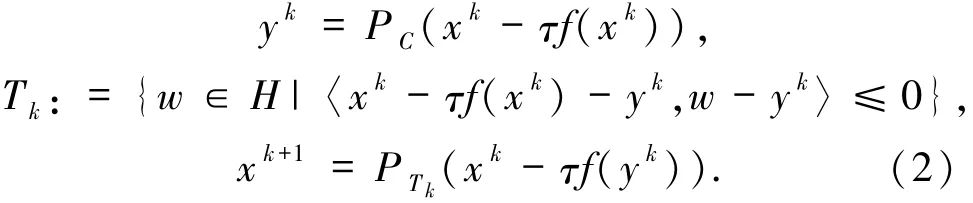
在映射f是單調(diào)和Lipschitz連續(xù)且Lipschitz系數(shù)為的條件下，證明了上述算法在Hilbert空間中的弱收斂性.接著，為了得到強收斂性，Censor等［6］又提出一種新的次梯度外梯度算法：

其中Tk與（2）式中相同.在f是單調(diào)和Lipschitz連續(xù)且Lipschitz系數(shù)為的條件下，證明了算法在Hilbert空間的強收斂性，但這個算法仍然需要計算一次向閉凸集C的投影，同時對映射f的Lipschitz系數(shù)的大小也有要求.

最近，He等［7］提出一種修正次梯度外梯度算法：

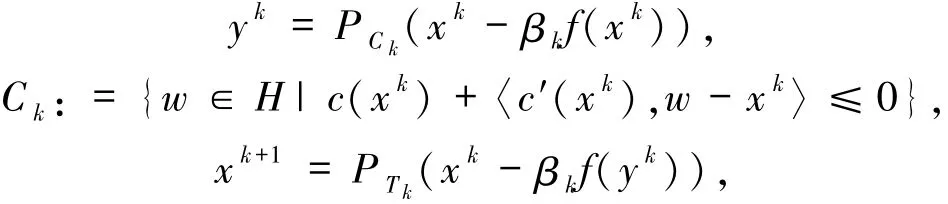
其中Tk與（2）式中相同.這個算法的兩次投影均是向特殊結構的半空間投影，同時要求其中的βk滿足恰當?shù)木€性搜索條件，從而不需要知道映射f的Lipschitz系數(shù)的大小，但只能得到該算法在Hilbert空間中的弱收斂結果.

受到文獻［6-7］的啟發(fā)，本文在文獻［6］的基礎上，將（3）式中向C的投影換成向文獻［7］中的Ck投影，并選取與文獻［7］相同的線性搜索條件，得到一種改進次梯度外梯度算法.當映射f滿足單調(diào)和Lipschitz連續(xù)且Lipschitz系數(shù)大小未知的條件時，本文能得到該算法在Hilbert空間中的強收斂結果.同時，在算法迭代的過程中，只需要計算向特殊結構的半空間的投影，避免向一般閉凸集投影，計算更加容易.

1 預備知識

本節(jié)給出一些基本定義和引理.設H是Hilbert空間，C是H中的非空閉凸子集.｛xk｝強收斂到x記為xk→x，｛xk｝弱收斂到x記為xk?x.

定義1.1設C?H為非空閉凸子集，對?x∈H，定義

為x在C上的投影.

定義1.2設凸函數(shù)c：H→R.c在x∈H處的次微分定義為

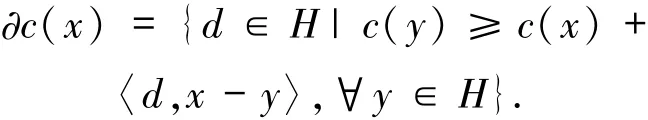
定義1.3設函數(shù)c：H→R.稱c在x處是Gateaux可微的，若x∈H，c′（x）∈H滿足

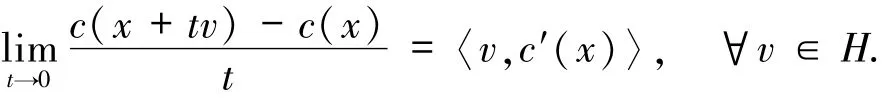
記c′（x）為c在x處的Gateaux導數(shù).

定義1.4設函數(shù)c：H→R，稱c在x處是弱下半連續(xù)的，若xk弱收斂于x時有

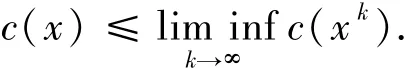
定義1.5設映射f：H→H，稱f是

1）Lipschitz連續(xù)的，若存在L＞0使得

2）單調(diào)的，若

定義1.6設C?H，則C在v∈C處的法錐NC（v）定義為

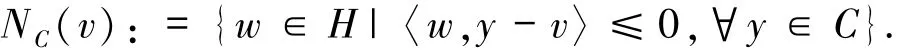
定義1.7設是H上的集值映射，則T是極大單調(diào)算子當且僅當滿足

1）T是單調(diào)的即〈u-v，x-y〉≥0，?u∈T（x），v∈T（y）；

2）T的圖像G（T）：＝｛（x，u）∈H×H｜u∈T（x）｝不包含于任何其他的單調(diào)算子的圖像中.

引理1.1［8］設f：C→H是Lipschitz連續(xù)單調(diào)算子，定義

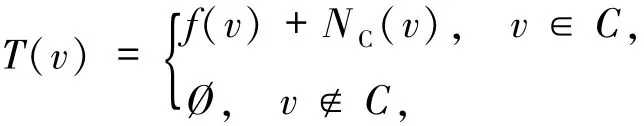
則T是極大單調(diào)算子.并且0∈Tv當且僅當v∈SOL（C，f）.

引理1.2［9］任何Hilbert空間都具有Kadec-Klee性質(zhì)，即是在H空間中的序列｛xk｝∞k＝0，如果滿足xk?x且‖xk‖→‖x‖，則有‖xk-x‖→0.

引理1.3［10］設凸函數(shù)c：H→R，則c在H上是下半連續(xù)的當且僅當c在H是弱下半連續(xù)的.

引理1.4［10］設凸函數(shù)c：H→R.如果c在x處是Gateaux可微和次可微的，則有?c（x）＝｛c′（x）｝.

引理1.5［11］設D?H為非空閉凸子集，則對?x∈H，y∈D，有

引理1.6［12］假設VI（C，f）的解集SOL（C，f）非空，x*∈C，則當x*∈SOL（C，f）時有以下2個條件的一個成立.

2 算法及收斂性分析

在本節(jié)中，非空閉凸集C定義為

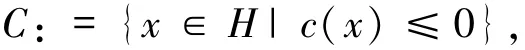
其中c：H→R是一個凸函數(shù).同時在本文中，總假設下列條件滿足：

條件2.1變分不等式VI（C，f）的解集SOL（C，f）非空.

條件2.2f：H→H是單調(diào)和Lipschitz連續(xù)的映射.

條件2.3函數(shù)c：H→R滿足以下條件：

1）c（x）是凸函數(shù)；

2）c（x）在H上是下半連續(xù)的；

3）c（x）在H上Gateaux可微的，且c′（x）在H上是M1-Lipschitz連續(xù)映射；

4）存在M2＞0使得‖f（x）‖≤M2‖c′（x）‖，?x∈?C，?C是C的邊界.

注1條件2.3來源于文獻［7］，這是為了給出算法中的線性搜索條件，同時在算法的收斂性證明過程中也有重要作用.

算法2.1（改進次梯度外梯度算法）

步0：?x0∈H，令k＝0.

步1：構造半空間

計算

這里的βk＝σρm k，σ＞0，ρ∈（0，1）.mk為滿足下式的最小正整數(shù)：

其中M＝M1M2，ν∈（0，1）.

步2：構造半空間

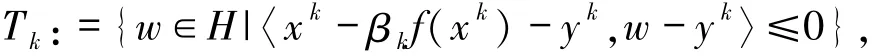
計算

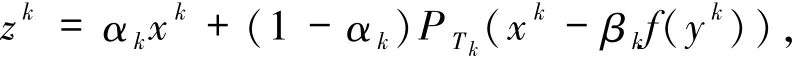
步3：令

計算

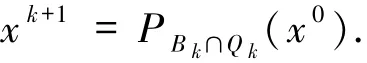
步4：令k＝k+1返回步1.

注2算法中Bk和Qk的構造來源于文獻［4］，與文獻［5］相比這樣做的好處在于只增加一次向超平面交的投影就能得到算法的強收斂性結果.

注3在算法2.1中，對任意的x∈C，都有

因此C?Ck.

又根據(jù)引理1.5和yk＝PC k（xk-βkf（xk））有因此Ck?Tk.

為了證明算法2.1的收斂性，首先必須證明下面的引理.

引理2.1假設條件2.1-2.3成立.則由算法2.1生成的序列有界.

證明對所有的k≥0，容易看出Bk和Qk是閉凸集.再根據(jù)Qk的定義可得

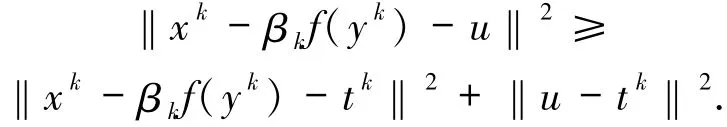
因此

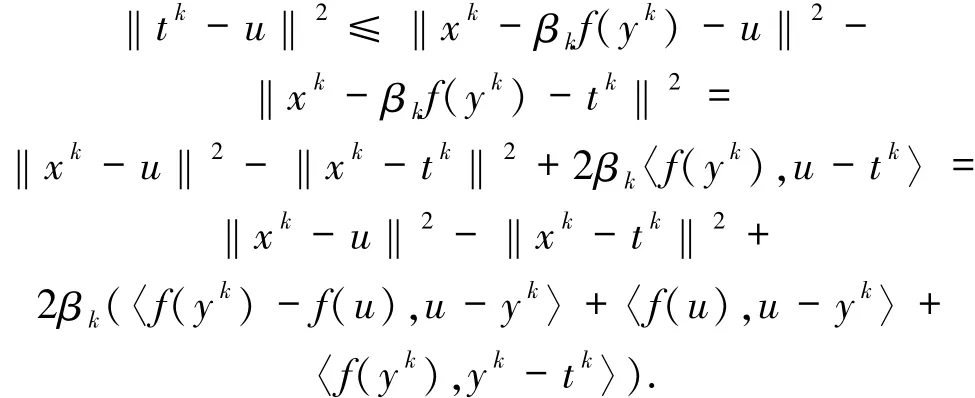
再由條件2.2有

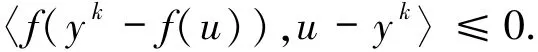
因此

為了證明u∈Bk，即‖zk-u‖2≤‖xk-u‖2，下面分兩種情況討論：

情況1f（u）＝0，則有

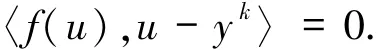
因此

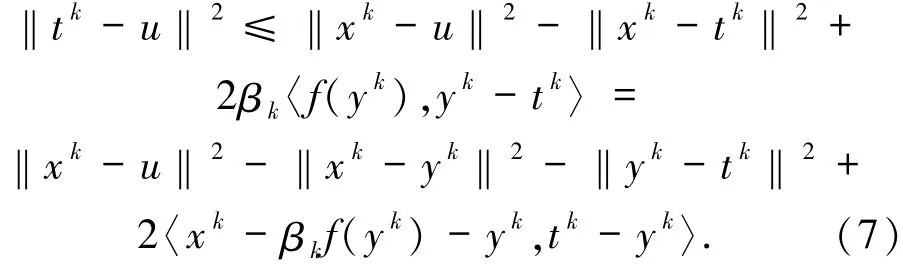
根據(jù)Tk的定義和tk∈Tk有

因此

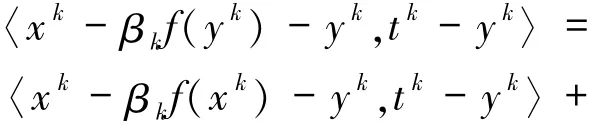
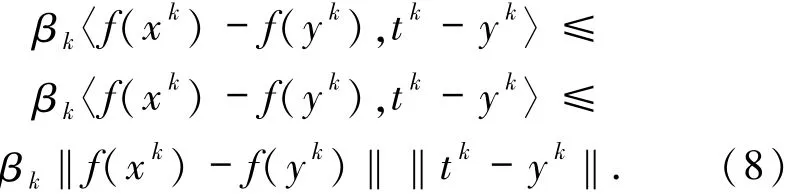
將（8）式代入（7）式中可得

又根據(jù)（4）式可得

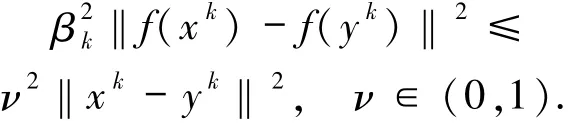
因此（9）式可化為

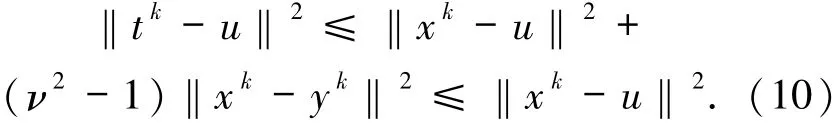
情況2f（u）≠0.根據(jù)引理1.6可知，存在α＞0，使得f（u）＝-αc′（u）.由次微分不等式

u∈?C，c（u）＝0可得

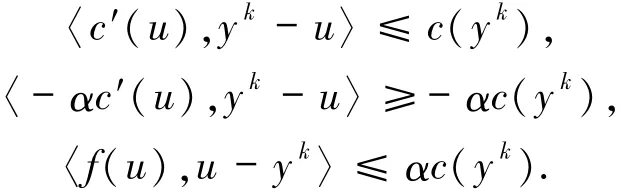
又因為yk∈Ck，即

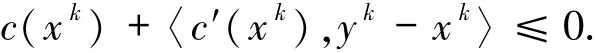
c′（x）在H上可微

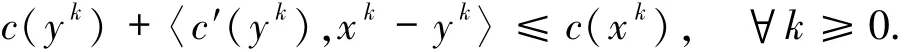
上兩式相加可得

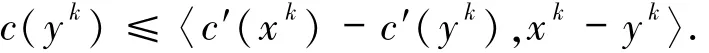
再根據(jù)條件2.3有

將（11）式代入（6）式中可得

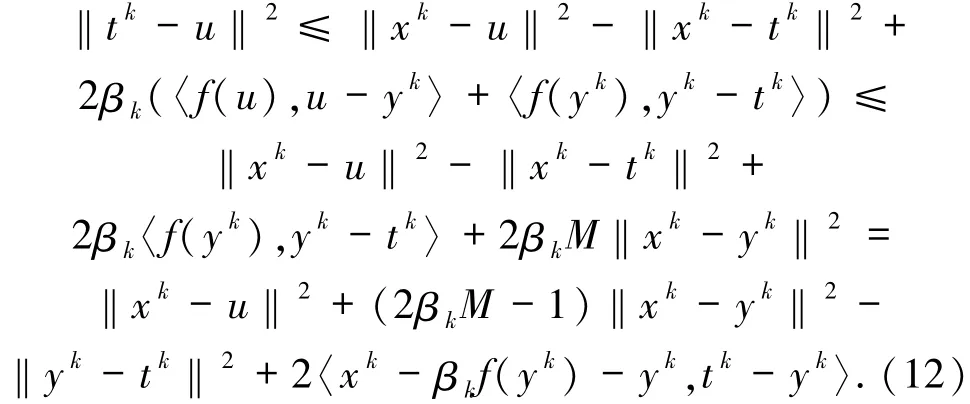
將（8）式代入（12）式中可得

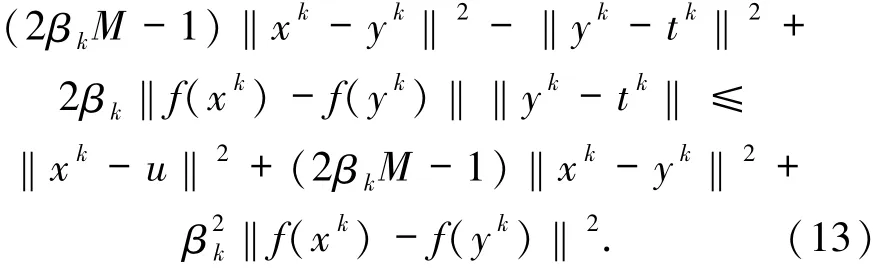
根據(jù)（4）式可將（13）式化簡為

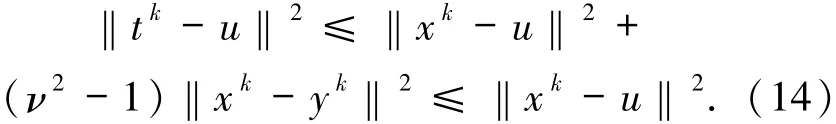
與情況1所得的不等式相同.再由zk的定義可知

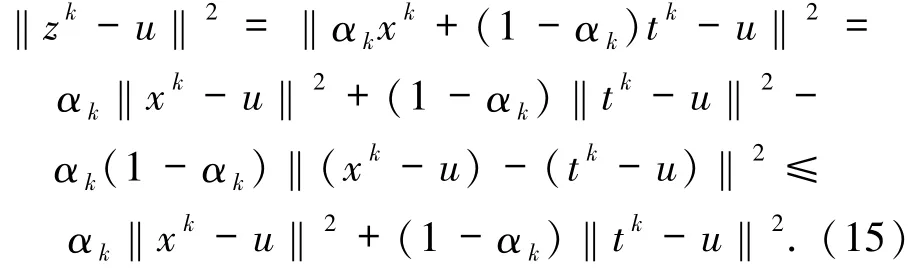
將（10）式（或（14）式）代入（15）式中可得

根據(jù)（16）式以及Bk的定義可知u∈Bk，?k＞0.

下面利用歸納法證明u∈Bk∩Qk.

當n＝0，Q0＝H.則u∈B0∩Q0＝B0，顯然成立.

當n＝k時，關系式成立，即u∈Bk∩Qk.下面去證明u∈Bk+1∩Qk+1成立.

由算法可知xk+1＝PB k∩Q k（x0），因此有

令z＝u∈Bk∩Qk，則

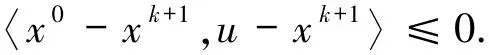
因此u∈Qk+1，u∈Bk+1∩Qk+1.即u∈SOL（C，f）?Bk∩Qk，?k＞0.令u*＝PSOL（C，f）（x0），因為u*∈SOL（C，f）?Bk∩Qk，xk+1＝PB k∩Q k（x0）.因此

定理2.1假設條件2.1-2.3成立.則由算法2.1生成的2個序列強收斂到SOL（C，f）中的一點u*，并且

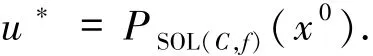
證明首先條件2.1-2.3滿足，則有引理2.1成立，即有界，易得也有界.由（5）式和xk+1∈Qk可得

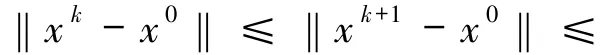
利用引理1.5和（5）式，令D＝Qk，x＝x0，y＝xk+1可得

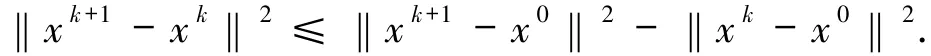
令k→∞，則有

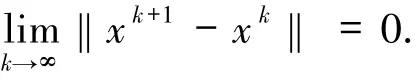
又因為xk+1∈Bk，即

由三角不等式可得

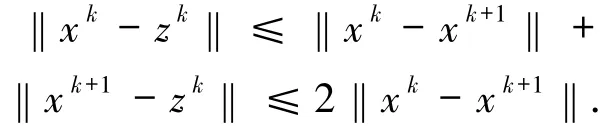
因此

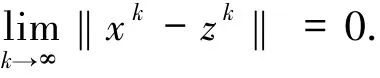
由（16）式可知

即

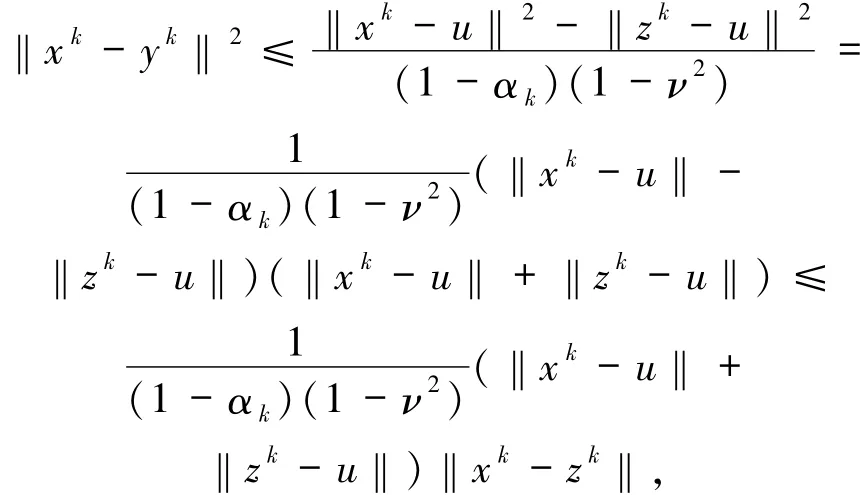
其中αk，ν∈（0，1），令k→∞，則有

由條件2.2可知

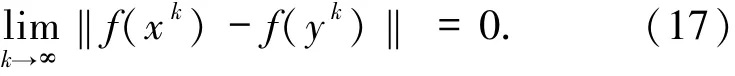
在情況1中，由（9）式有

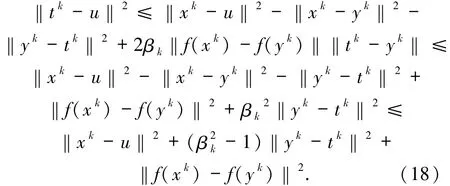
在情況2中，由（13）式有

又根據(jù)（4）式可得

將上式代入（19）式中可得到與（18）式相同的不等式.

再由（15）式有

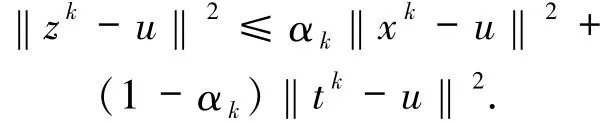
結合上兩式有

因此

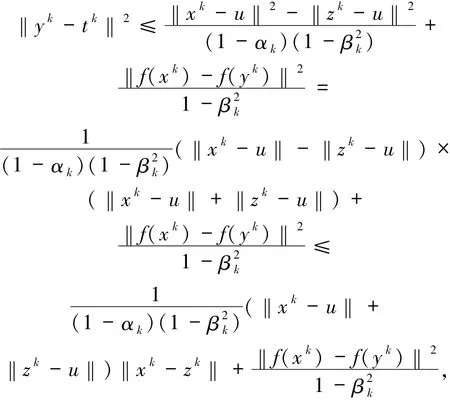
其中αk，βk∈（0，1）.令k→∞，則有

由三角不等式

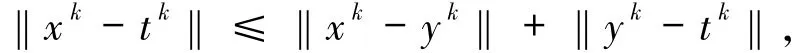
因此

下面首先證明x*∈C.根據(jù)yk∈Ck和Ck的定義可知

因此

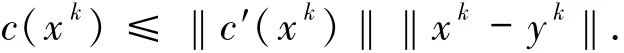
由條件2.3的3）可知，c′（x）在H的任意有界子集上是有界的，即存在M′＞0使得‖c′（xk）‖≤M′，?k≤0.因此

又由條件2.3的2）可知c是下半連續(xù)的，根據(jù)定義1.4和引理1.3得

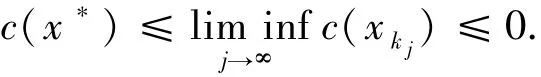
因此x*∈C.接下來證明x*∈SOL（C，f）.令（v，w）∈G（T），由引理1.1則有w∈T（v）＝f（v）+NC（v），因此

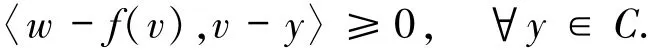
令y＝x*，則有

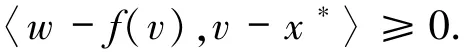
又由yk＝PC k（xk-βkf（xk）），因此

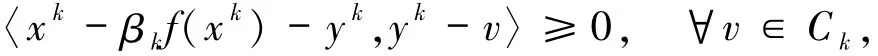
即

因此

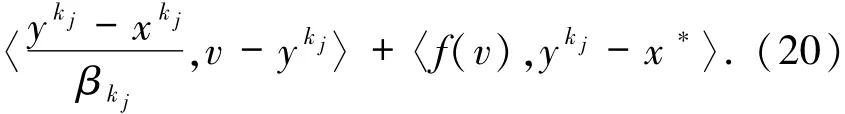
最后一個不等式根據(jù)f的單調(diào)性得出.

由于xk j?x*，則根據(jù)（17）式可知yk j?x*.在（20）式中令j→∞可得

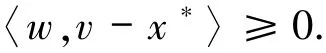
因為T是極大單調(diào)算子，因此x*∈T-1（0）＝SOL（C，f）.由定理已知條件u*＝PSOL（C，f）（x0），

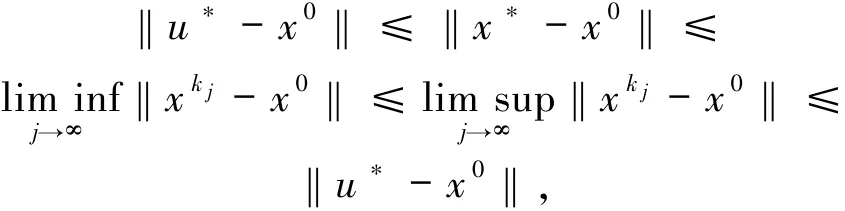
因此

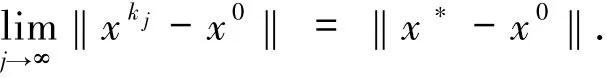
即‖xk j-x0‖→‖x*-x0‖，且xk j-x0?x*-x0.則根據(jù)引理1.2可得‖xk j-x*‖→0.

令j→∞可得

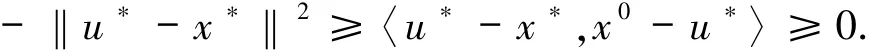
因此

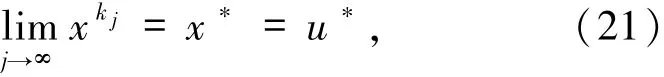
假設xk強收斂到u*不成立，則一定存在ε＞0和子序列使得

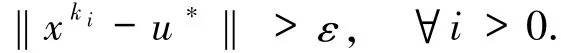
這與假設矛盾，因此xk→u*.

3 數(shù)值結果

在這部分內(nèi)容中，利用例4.1給出算法2.1的計算機檢驗結果，同時與文獻［7］的中的算法2.4（MSubEGM）和文獻［6］的中的算法2.6（Censor）做比較.這些結果是用Matlab在CPU型號為2.0 GB的筆記本電腦上運行的.在算法2.1和算法MSub-EGM中，均取σ＝1，ρ＝0.6，ν＝0.8，M＝0.2，αk＝0.4.在算法Censor中，取τ＝0.4，αk＝0.4.用iter來記迭代的步數(shù)，CPU來記運行所花費的時間，算法的終止條件為‖xk-yk‖≤ε.

例3.1定義

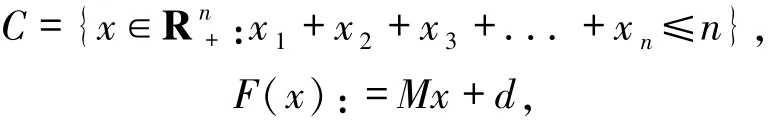
其中

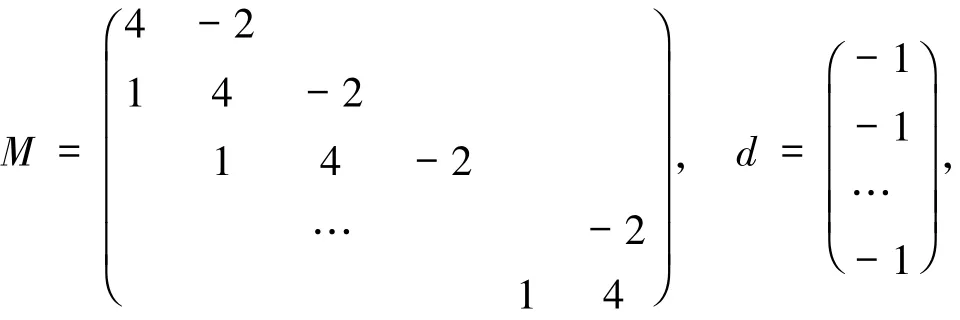
初始點x0＝（0，…，0）.

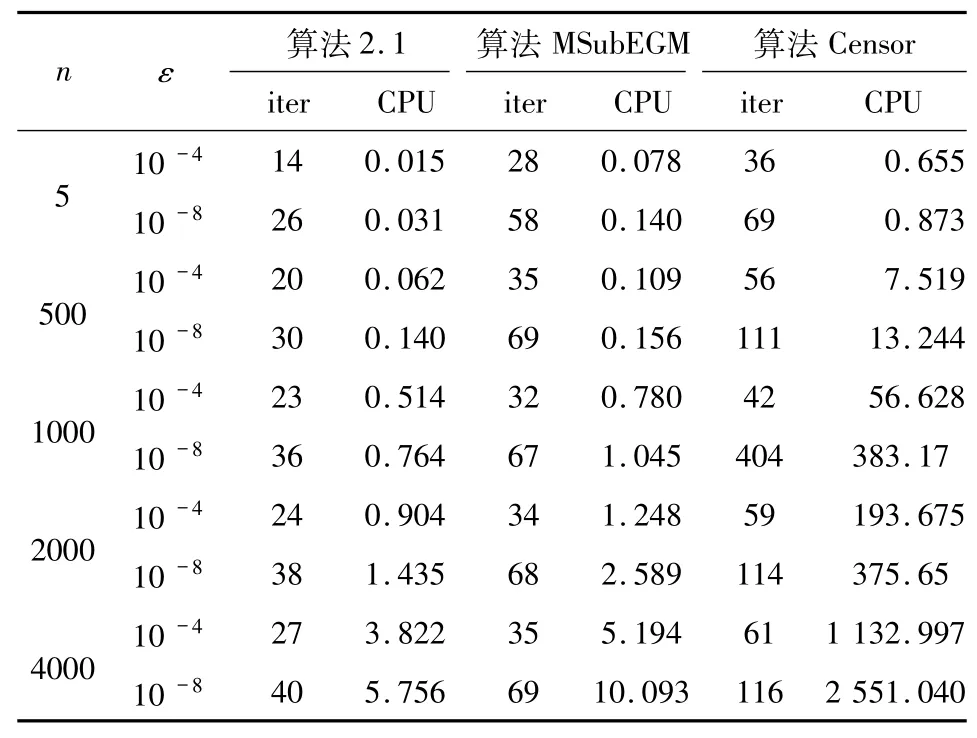
表1 例3.1的數(shù)值結果Tab.1 Numerical results of Example 3.1