實踐“自主·合作·交流”教學新樣態
——以圓錐曲線的共同特征為例*

徐進勇 (廣東省廣州市第九十七中學 510260)

新課程標準倡導獨立思考、自主學習、合作交流等多種學習方式，強調學習是學生與情境、問題的有效互動，突出學生個性化、多樣化的學習和發展需求，提高學生交流、合作的社會溝通能力，著力發展數學核心素養．[1]新課堂樣態應該是一種“自主·合作·交流”型的學習組織，它既是一種課堂形態，也是一種課堂理念、課堂結構與學習機制．這種新樣態課堂能將學生的外趨要求轉變為內驅動力，將學生的被動學習轉變為主動求索，奠定自主學習的基礎，并真正建立起師生互動與共享的共同體以促進知識的流動與創新，達成學生個人成長與課堂團隊整體進步的雙贏目的．

“圓錐曲線的共同特征”一節在人教A版沒有專門列出，只是在例題或習題中“隱約”出現，很多教師也就不再組織學習．筆者認為“圓錐曲線的共同特征”是學習圓錐曲線后的一節很好的復習提高課，值得研究．如何才能上好這節課呢？是直接給出定義強化理解，還是讓學生“自由發揮”？一番思考后，筆者決定創新課堂樣態．

1 教學設計

1.1 課前任務布置

情境1 公元前3世紀，古希臘學者阿波羅尼斯用一個圓錐，通過改變截面的位置產生橢圓、雙曲線、拋物線三種曲線(圖1)．阿波羅尼斯從幾何圖形的角度來研究圓錐曲線性質，但由于過多地依賴圖形而給研究帶來了困難．17世紀，法國數學家笛卡爾提出點的坐標和變數思想，把幾何曲線轉化為代數方程，通過研究方程來揭示曲線的性質，創立了解析幾何．

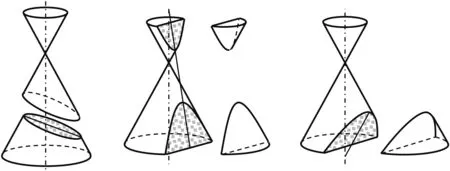
圖1

情境2 圓錐曲線不僅在數學歷史發展的過程中熠熠生輝，在科學文化的其他領域也閃爍光芒．如當人造天體被以不同的速度(三種宇宙速度)從地球發射出去的時候，它的軌跡分別是圓、橢圓、拋物線和雙曲線(圖2)，這就是物理中所講的開普勒三大定律．

情境3 嫦娥四號于2018年12月8日在西昌衛星發射中心發射成功，在降落月球背面過程中要經過多次變軌，變軌的實施要通過數據的輸入和動力制動完成(圖3)．嫦娥四號實現了人類首次月球背面著陸，創造出“世界先驅者”般的成就與壯舉．

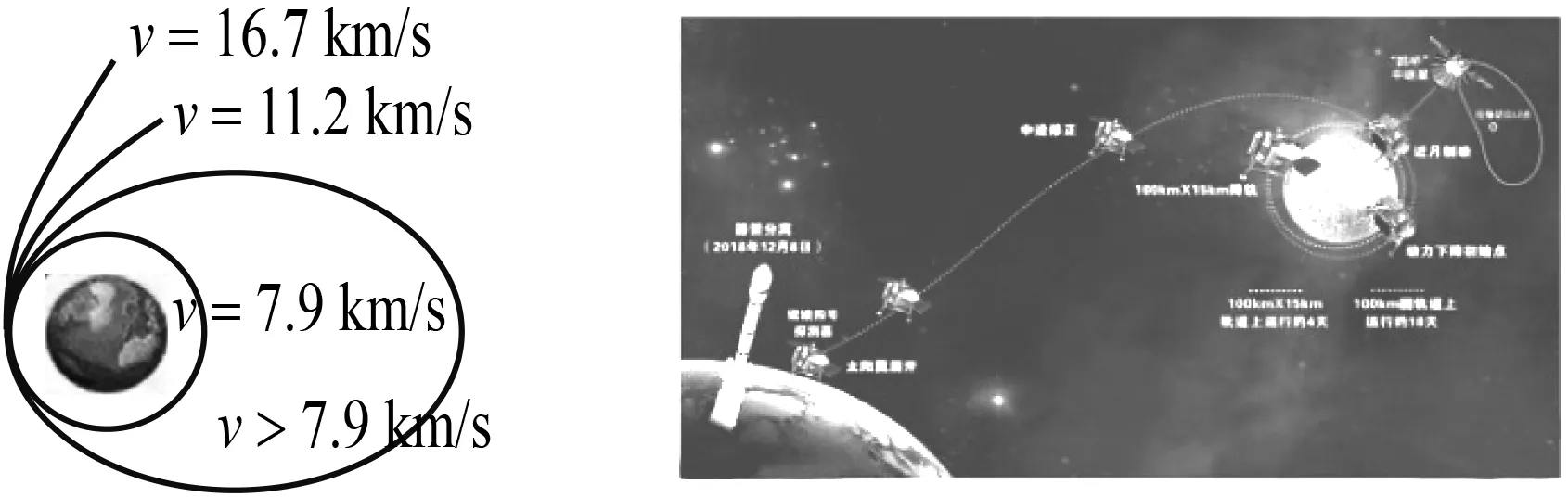
圖2 圖3

問題橢圓、雙曲線、拋物線圖象的形成過程存在著密切聯系，三種曲線相聯的背后存在怎樣的數量關系？

任務：請各位同學結合課本內容或搜集相關材料作總結或猜想，尋找三種曲線在數量上的聯系與特征，探尋它們內在的統一性，并按“已有材料-猜想探索-得出結論-自我評價”的形式書寫研究報告．

1.2 課堂交流展示

教師閱讀學生上交的報告，發現研究方向主要聚焦三類：(1)從橢圓、雙曲線定義出發思考(以下簡稱為“定義”)；(2)研究斜率間關系(以下簡稱為“斜率”)；(3)研究到定點與到定直線的距離比(以下簡稱為“距離”)．全班35人中研究方向大致可分為：定義法9人，斜率法6人，距離法20人．上課時按“同質”組合就座形成學習小組，前10分鐘在同學習小組內交流彼此想法，加深理解，形成共識；接下來20分鐘由各小組推選的匯報人通過實物投影展示研究成果；后10分鐘師生共同研討，反思提高．

學習小組1 從“定義”探索．

已有材料：到兩個定點的距離和為定值(大于兩定點間距離)的點的軌跡是橢圓；差的絕對值為定值(小于兩定點間距離)的點的軌跡是雙曲線；商為定值(不為1)的點的軌跡是圓(稱阿波羅尼斯圓)，商為1的點的軌跡是直線．

猜想：到兩個定點距離積為定值的點的軌跡是拋物線嗎？如果是，那就太完美了！

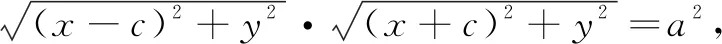
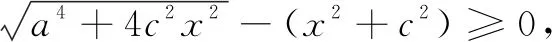
但還是很難通過描點法畫出它的圖象，于是想到用幾何畫板畫圖：如圖4，不斷改變a,c的大小關系，得到恰似一個細胞分裂成兩個細胞的過程圖，非常奇妙！

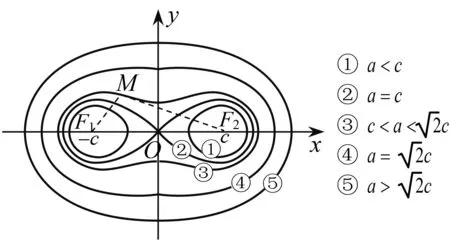
圖4

通過上網搜索定義：這些曲線實際上是數學史上著名的卡西尼卵形線．在數學史上，到兩個定點(叫做焦點)的距離之積為常數的點的軌跡稱為卡西尼卵形線.卡西尼是一位出生于意大利的法國籍天文學家和水利工程師，他是第一個研究土星的人，為了紀念卡西尼對土星研究的貢獻，人們用他的名字命名了用于探測土星的探測器．

得出結論 雖沒達到尋找橢圓、雙曲線、拋物線數量上的統一，但有意外驚喜，發現了卡西尼卵形線，明確了到兩個定點的距離和、差、積、商為定值時各自點的軌跡．

自我評價 建系列方程，用方程研究曲線，幾何畫板幫助畫圖，網上查詢資料，感受卡西尼卵形線很美．

學習小組2 從“斜率”探索．

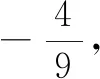
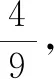
(3)(課本42頁)已知點A,B的坐標分別為(-1,0),(1,0)，直線AM,BM相交于點M，且直線AM的斜率與直線BM的斜率的商是2，求點M的軌跡方程．答案：x=-3(y≠0)．

(4)(課本74頁)已知點A,B的坐標分別為(-1,0),(1,0)，直線AM,BM相交于點M，且直線AM的斜率與直線BM的斜率的差是2，求點M的軌跡方程．答案：y=1-x2(x≠±1)．

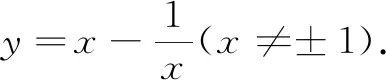
猜想：到兩個定點斜率之差為定值的軌跡一定是拋物線嗎？

已知點A,B的坐標分別為(-a,0),(a,0)，直線AM,BM相交于點M，且直線AM的斜率與直線BM的斜率的差是2c，探求點M的軌跡方程．

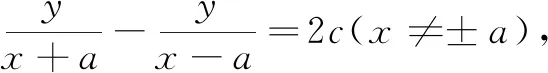
得出結論 與兩個定點連線的斜率之積大于0時點的軌跡是雙曲線；斜率之積小于0時(不為-1)軌跡是橢圓；斜率之積等于-1時軌跡是圓；斜率之差為定值時軌跡是拋物線．(都要去掉兩個點)

自我評價 通過斜率找到橢圓、雙曲線、拋物線間的數量關系，但由于斜率的條件限制，所得軌跡中都要去掉兩個點，而且得出的拋物線也不是標準型，有點遺憾；認真搜集課本相關內容，通過對比能發現一些有價值的規律；從和、差、積、商的運算變化中收獲新的知識；注意解題中的條件限制與等價變化．

學習小組3 從距離探索．

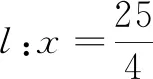
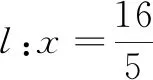
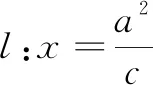
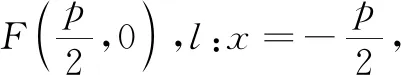
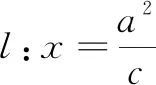
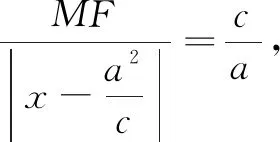
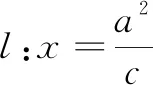
自我評價 找到了三種曲線數量上的聯系，而且距離比e分別為(0,1),1,(1,+∞)的連續變化，與圖形的連續變化相吻合，很開心；課本習題從(1)到(3)由特殊到一般，循序漸進；仿照課本中橢圓方程的推導過程，令a2-c2=b2，使方程化簡，形式簡潔，有對稱美！

1.3 師生互動

展示匯報環節結束后，教師充分肯定學生的猜想及所使用的數學研究方法(用方程研究曲線)，走的路不同，欣賞到的風景也就不同，但彼此交流，讓我們看到很多，想到很多！

師：針對小組3的結論，你能用更簡潔的語言表達嗎？

生：橢圓、雙曲線、拋物線可統一為平面上到一定點的距離與到不過該定點的定直線的距離之比為常數e的動點的軌跡．

師：據此，你能求出這種統一定義下的方程嗎？

如何建系，如何設點和定直線方程？方法很多，方程的形式也不同．瑞士數學家歐拉是以定點為坐標原點，定直線方程設為x=-p，此時方程是什么？學生很快計算得出(1-e2)x2+y2-2pe2x-p2e2=0．

師：用幾何畫板展示三種曲線的連續變化圖，并說明用幾何畫板的制圖原理(進一步突出統一 定義)．

1.4 課堂小結

平面上到一個定點的距離和到一條定直線的距離之比是一個常數e的點的軌跡是圓錐曲線，統一方程可寫為(1-e2)x2+y2-2pe2x-p2e2=0．研究讓我們看到,只有抓住共同的本質，才能用統一的觀點、統一的語言來描述不同的事物．這讓我們有一種“透過現象看本質”的快感，使我們領略到數學的“統一美”．

2 課堂新樣態特征分析

2.1 課堂教學要充分尊重學生思維

好的數學教學活動應突出數學的特點和學生的思考，揭示數學知識產生的自然性與合理性，要基于感性發展理性．本節課的設計就是突破“直接化”的方案，在情境與問題的驅動下，突出學生的自然想法，如定義中到兩個定點的距離和、差、商研究了，為什么不研究“積”？嫦娥四號變軌的實施要通過數據的輸入和動力制動完成，那么圓錐曲線圖形連續變化背后的數據又是什么呢？橢圓與雙曲線定義、性質聯系較為緊密，似乎與拋物線有些疏遠，拋物線有準線，橢圓與雙曲線為何沒有？等等．不同的疑問，有不同思考；不同的人，有不同的思維方式；不同基礎的學生，有不同的思維層次．但所有學生都是在探究自己想要解決的問題.學習有興趣，主動性就很強，經歷過探究過程，才能積累知識和方法，獲得理智和情感體驗，這就是最好的學習方式．尊重學生思維的教學要做好以下幾點：(1)充分了解學生已有的認知基礎，如課前教師要認真批閱學生的研究報告或作業，明確學生的認知起點；(2)尊重學生的情感起點，即教師要明白學生想知道什么、渴望解決什么；(3)尊重學生對知識建構的思維習慣，關注新舊知識之間的聯系，形成自然的思維發展鏈條，如教師針對學習小組3所進行的適時拓展；(4)尊重學生個性差異，關注課堂新的生成，允許并鼓勵學生的個性思維在課堂流淌，本節課安排3個小組分別展示，就是充分尊重學生的個性化思維，使課堂煥發出活力．

2.2 著力培養學生的自主發展能力

教學中教師先創設學習情境，提出目標與任務.學生課后學習的空間與時間是開放的、自由的，帶著自己的疑問查閱課本或上網搜集資料，也可以借助其他工具(如幾何畫板)進行自主學習.這一目的是要讓學生在學習中經歷：觀察分析數學事實，提出有意義的數學問題；搜集整理相關素材，歸納猜想、探求適當的數學結論或規律；給出科學合理的解釋或進行理性的證明；反思探索過程，通過檢驗優化研究方案，從而獲得進一步學習以及未來發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗(四基)，提高從數學角度發現和提出問題的能力、分析和解決問題的能力(四能).與傳統式學習相比，“自主·合作·交流”型學習更強調學習主體對材料的搜集與感悟，強調研究小組或團隊的合作交流與共同進步，這些都是新時代公民必備的素養．因此，教學中教師要充分相信學生、引導學生，逐步引領學生走上自主學習與發展的道路．

2.3 合作交流是新樣態課堂的主旋律

課堂教學是課堂活動的教學，課堂活動包括師生交流、展示、探究等．葉瀾教授認為，在教學過程中，教師不僅要把學生看作“對象”“主體”，還要看作是教學“資源”的重要構成和生成者．學生在課堂活動中的狀態，包括他們的學習興趣、積極性、注意力，學習方法與思維方式，合作能力與質量，發表的意見、建議、觀點，提出的問題與爭論乃至錯誤的回答等，無論是以言語還是以行為、情緒方式的表達，都是教學過程中的生成性資源．有了這種“活資源”的意識，教師才不會把學生在課堂中的活動、回答看作是一種對教師教的配合，而是看作對教的過程的積極參與和教學過程創生的不可缺少的重要組成部分．[1]本節課的教學設計主旨就是學生的3種不同研究方向、方式、結果通過分組展示給全班同學，并讓各種意見獲得充分解釋，使學生在交互學習中完全明了背后的道理．正如美國小說家華萊士所指出的，教育的目的，不是學會一堆知識，而是學會一種思維的方式．教師在教學中要積極為學生創建交流互動的平臺，讓學生敢說、會說且說得精彩，真正實現教師組織下的學生思維資源的共賞，體現學習不僅是個體的行為，也是集體努力的結果．

2.4 努力實現課堂教學中的文化育人

文化屬性是課程知識的基本屬性，挖掘課程知識的文化元素，充分表達知識的文化屬性，是課堂教學中文化育人方式的前提條件．本節課的教學設計從歷史和現實兩種情境揭示知識的文化屬性，通過“自主·合作·交流”展示學生不同的思維歷程來表達教學過程作為一種文化實踐的過程，并突出其中的人與事，切實在學生的知識學習過程中開展文化導入，引導學生開展文化體驗、文化體認、文化體悟，感受數學的形式美、統一美、簡潔美，并在探索過程中發展學生的數學文化積淀、人文素養和人文情懷．課堂教學不應僅僅把知識作為一種事實或結論告訴或傳遞給學生，還需對具體知識進行深入的文化分析，引導學生探究知識的文化屬性、文化思想、文化精神和文化思維方式，體現知識對學生的文化影響力，真正達成“以文化人”的目的．[2]