2020年浙江省高中數(shù)學(xué)競賽解析幾何題的探究及推廣

吳 江 (浙江省杭州市交通職業(yè)高級中學(xué) 310011)

1 問題呈現(xiàn)

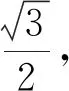
(1)求橢圓C的方程；

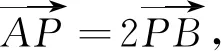
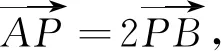
2 解法探究

(1)橢圓C的方程為x2+4y2=1．

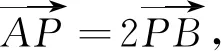
評析對于直線與橢圓相交問題，自然會想到設(shè)直線方程和交點，然后聯(lián)立方程運用韋達定理．不等關(guān)系來源于判別式大于零，由此得到關(guān)于m和λ的不等式，再通過含有4個未知數(shù)的三個方程來找到m和λ的等量關(guān)系，從而建立關(guān)于λ的不等式．

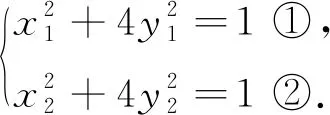
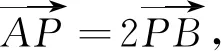
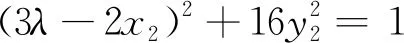
評析在這一解法中并未引入新的變量，而是直接將題干中涉及的變量所滿足的關(guān)系全都呈現(xiàn)出來，得到關(guān)于五個未知數(shù)的四個方程，最終通過消元轉(zhuǎn)化可以得到x2和λ的等式關(guān)系，從而由x2的范圍來確定λ的范圍．此方法計算量小，方程思想起到了指導(dǎo)性作用．

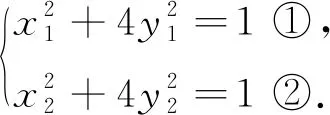
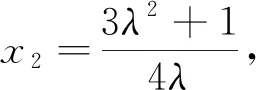
評析點差法是先作差再代入，而解法2是先代入再作差，其用意是不同的．點差法的關(guān)鍵在于根據(jù)(*)式配比好系數(shù)，然后作差，從而消去變量得到x2和λ的等式關(guān)系，起到“設(shè)而不求”的效果，減小了計算量．

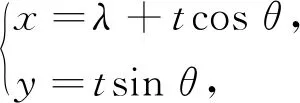
評析由題意不難發(fā)現(xiàn)點P是線段AB的三等分點．處理此類問題，直線的參數(shù)方程是常用方法，其基礎(chǔ)是要理解直線參數(shù)方程的意義，尤其是理解方程中參數(shù)的含義，要做到數(shù)形結(jié)合，才能游刃有余．

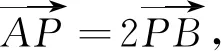
評析橢圓參數(shù)方程將點B坐標表示為關(guān)于θ的形式，再利用向量關(guān)系得到坐標關(guān)系，由此得到點A坐標表示，將其代入橢圓方程得到θ與λ的關(guān)系，最后回歸到x2與λ的等式關(guān)系，由此建立不等式．運用橢圓參數(shù)方程實則是運用了點在橢圓上及三角恒等關(guān)系，往往能夠起到簡化計算的效果．

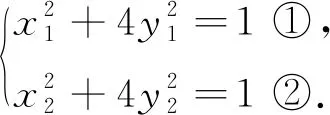
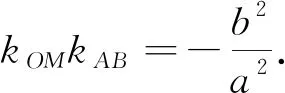
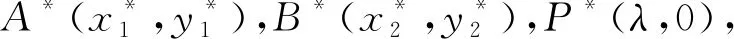
評析圓有許多好的性質(zhì)，將橢圓仿射成圓，線段間的比例關(guān)系保持不變，可以找到仿射交換后兩個交點間的坐標關(guān)系；再利用垂徑定理作為思路方向，建立變量之間的聯(lián)系．仿射交換的運用也體現(xiàn)了數(shù)形結(jié)合的思想．

解題反思圓錐曲線中的取值范圍問題已然成為了高考和競賽的熱點，此類題目往往蘊藏了多個切入口，要弄清楚解法的本質(zhì)是什么才能有所感悟.設(shè)線其實是設(shè)了角的正切值，設(shè)參數(shù)方程其實是設(shè)了角的正弦值和余弦值，其本質(zhì)都是設(shè)角，所以雖然方法多樣但是往往又殊途同歸．此類問題的思考方向大致可分為兩個:函數(shù)和不等式.函數(shù)中又可分為兩類，一類是直接可以快速判斷函數(shù)的單調(diào)性，另一類是需要對函數(shù)求導(dǎo)后再來判斷單調(diào)性．不管是哪種方向，最終還是要回到“已知范圍求范圍”，在此過程中，考查了學(xué)生的數(shù)學(xué)基本功和對數(shù)學(xué)思想方法的運用能力．

3 問題推廣

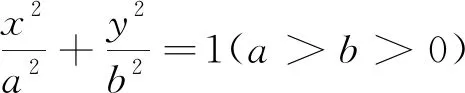
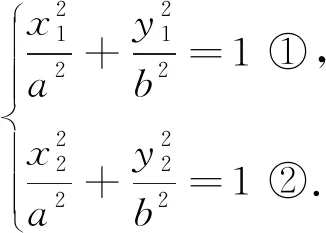
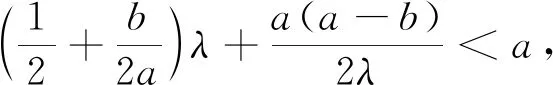
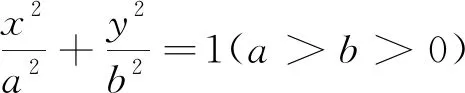
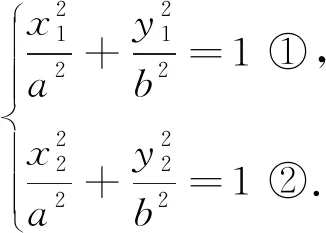
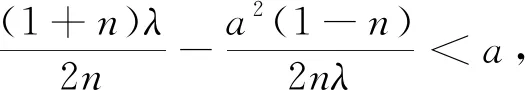
4 感悟反思

好的問題往往解法不唯一.我們可以從不同角度去看待分析，挖掘其本質(zhì)，通過引導(dǎo)學(xué)生一題多解，歸納總結(jié)，加深對知識的理解，感受各種解題方法背后所蘊含的數(shù)學(xué)思想．抓住其本質(zhì)特點對一道題完成一題多解便是完成對一類題的探究，起到舉一反三、觸類旁通的效果．但是，最終仍需要從一題多解回歸到多題一解，以便在遇到問題時快速預(yù)判，選擇合適的方法去解決，真正提高學(xué)生的綜合數(shù)學(xué)能力及數(shù)學(xué)核心素養(yǎng)．