超高速碰撞下蜂窩夾層板結構優化設計研究

袁小雅，馬天寶

(北京理工大學爆炸科學與技術國家重點實驗室，北京 100081)

蜂窩夾層板[1]作為防護結構被廣泛應用于航空航天領域，在衛星板式結構中的應用可占80%以上。蜂窩夾層板由上、下面板及中間的蜂窩芯子構成，具有比剛度、比強度高、抗疲勞、減振隔聲，吸熱隔熱等優點。面板通常采用鋁合金、碳纖維、凱芙拉、玻璃布等材料，蜂窩芯子一般采用鋁或芳綸紙材料。

國內外許多學者對蜂窩夾層板的超高速碰撞特性進行了研究。Turner、Taylor等[2]對帶隔熱層的單蜂窩夾層板及雙蜂窩夾層板結構進行了大量超高速碰撞試驗。在此試驗數據基礎上，Taylor等[3]利用AUTODYN軟件，應用Lagrange單元、殼單元和SPH粒子結合的方法，分別在2D和3D情況下對碎片超高速碰撞蜂窩夾層板的撞擊過程進行了數值模擬，并與試驗數據進行了對比。徐小剛等[4]采用APDL語言編制了蜂窩芯建模程序。賈光輝等[5]利用SPH-FE耦合的算法，對鋁蜂窩板結構被碎片正斜撞擊過程分別進行了數值模擬研究，就碰撞角度對碎片云運動、蜂窩芯子及蜂窩后面板損傷的影響進行了詳細分析。黃潔等[6]對帶隔熱層蜂窩結構開展了超高速碰撞試驗研究和數值模擬。單立等[7]采用SPH-FE耦合的方法對冰粒超高速碰撞蜂窩板結構進行了數值模擬研究。廖高健等[8]對輕質多孔火山巖彈丸超高速碰撞蜂窩夾層板進行了試驗研究。傳統有限元法難以模擬內結構胞壁在高速撞擊下的斷裂破碎過程，劉平等[9]發展了蜂窩夾芯結構的物質點建模方案，基于該模型模擬的多種撞擊工況均與實驗或經驗公式吻合。

超高速碰撞試驗受限于試驗條件與科研經費，其特性研究僅在物理試驗取得了少量成果，而數值模擬方法靈活經濟，越來越受到重視。本文首先建立了球形彈丸超高速碰撞蜂窩夾層板的有限元模型，采用最優拉丁超立方設計方法生成樣本空間，得到仿真結果后，構建設計變量與目標函數之間的Kriging近似模型，選取前面板厚度、單蜂窩芯格邊長、蜂窩芯子高度、壁厚作為優化變量，以最大化球形彈丸的動能損失、最小化蜂窩夾層板結構的面密度作為優化目標，利用存檔微遺傳算法(AMGA)進行優化，得到Pareto最優解集中的4組優解，為研究鋁蜂窩夾層板結構的超高速碰撞特性及空間碎片防護結構的優化提供進一步支持。

1 蜂窩夾層板超高速碰撞模型建立

1.1 幾何模型

蜂窩夾層板通常由上、下面板及中間的蜂窩芯子構成，蜂窩夾層板結構的面板與蜂窩芯子之間通過粘結劑相連。碎片超高速碰撞蜂窩夾層板結構的幾何模型如圖1所示。在設計蜂窩夾層板結構時，為了避免夾層板受載時的拉彎耦合效應和制造固化后引起的翹曲變形，前后面板一般采用相同材料及相同厚度。前面板厚度為tf，后面板厚度為tr，單蜂窩芯格邊長lhc，蜂窩芯子高度S，蜂窩芯子壁厚thc。

圖1 蜂窩夾層板結構的幾何模型示意圖

本文采用鋁合金球形彈丸來模擬超高速碰撞中的碎片。彈丸撞擊蜂窩夾層板的位置如圖2所示，撞擊位置為芯格的中心點。

圖2 彈丸撞擊蜂窩夾層板位置示意圖

1.2 計算模型及材料參數

采用SPH-FE耦合的方法對蜂窩夾層板的超高速碰撞過程進行數值模擬。球形彈丸與蜂窩夾層板的前后板劃分為SPH單元，蜂窩芯子劃分為Shell單元。面板與蜂窩芯子通過粘結劑連接，有學者在數值模擬中忽略粘結劑的作用，在不影響計算結果的前提下，建模時使面板和蜂窩芯子之間保持一個很小的間距[10]，本文采取間隔距離為0.01 mm。SPH單元與Shell單元間的作用關系采用接觸關鍵字*CONTACT_AUTOMATIC_NODES_TO_SURFACE定義。

蜂窩芯子的壁厚很薄，如果采用SPH方法對蜂窩芯子建模，為了保證整體數值模型的SPH粒子尺寸一致，整體數值模型的SPH粒子數量會大大增加，導致計算規模超出計算能力。除此之外，采用SPH法對蜂窩芯子建模時，蜂窩芯子會產生碎片，與彈丸、前后面板產生的碎片混在一起，持續對其他部分結構進行破壞，通過與試驗現象對比，這樣做不能準確的描述蜂窩芯子變形吸能的現象。引入有限元法中的Shell單元對蜂窩芯子建模，可以減小計算規模，較好描述超高速碰撞中蜂窩芯子吸能的真實情況。

在仿真建模時必須合理的控制SPH粒子與Shell單元的網格密度。一般在單層板的超高速碰撞仿真研究中建議至少要劃分10層SPH粒子來保證準確性。若在本文中對前后面板也采用此原則劃分網格密度，整個模型的SPH粒子數目會很多，導致計算模型規模過大，超出計算機的計算能力。因此，本文中每個SPH粒子直徑劃分為0.1 mm。

劃分Shell單元的網格時，為了與SPH粒子接觸良好，兩者之間單元大小不能相差過大。文獻[3]中采用的SPH粒子直徑與Shell單元邊長之比為1∶7，本文采用1∶4，則Shell單元網格劃分大小為0.4 mm。圖3為彈丸超高速碰撞蜂窩夾層板的有限元模型。

圖3 彈丸超高速碰撞蜂窩夾層板的有限元模型示意圖

球形彈丸的材料采用2017鋁合金，蜂窩夾層板前后面板的材料是鋁合金2024-T81，蜂窩芯子的材料是鋁合金5052-H19。前后面板、蜂窩芯子的本構方程均采用Johnson-Cook強度模型，狀態方程均采用Mie-Gruneisen方程。薄板超高速撞擊中材料破碎形成碎片云的過程，被認為是稀疏波導致的拉應力超過材料斷裂應力后材料不斷層裂破壞的過程，而狀態方程與強度模型均不能表征材料斷裂方面的特征，需要考慮在計算中引入失效模型。然而，SPH方法失效模型的選擇尚無具體結論，有研究者認為SPH方法中不需要材料失效模型，另一些研究者則采用最大拉應力或Grady失效模型[11]。球形彈丸與前后面板采用的SPH粒子建模，本文選取最大拉應力失效模型，蜂窩芯子材料的失效模型采用Johnson-Cook失效模型，具體材料參數[9]列于表1。

表1 材料參數

1.3 超高速碰撞數值模擬結果及分析

選取歐空局METOP衛星上的蜂窩夾層板結構作為數值模擬的初始模型，結構幾何參數如表2所示[3]。

表2 METOP蜂窩夾層板幾何結構參數 mm

為了對碎片超高速碰撞蜂窩夾層板的模型進行驗證，選取文獻[2]中的4個試驗工況作為本文仿真算例，由于試驗中蜂窩夾層板的前面板帶隔熱層，將隔熱層厚度等效為0.1 mm的前面板，則仿真算例的前面板總厚度之和為0.5 mm[3]，其他結構參數不變。通過LS-DYNA軟件對上述蜂窩夾層板結構進行4個試驗工況的數值模擬研究，仿真結果與試驗結果如表3所示。若有多個穿孔時，選取最大穿孔的直徑作為穿孔直徑，NP表示沒有穿透后面板。

表3 試驗結果與仿真結果

結果表明，4個工況的比較吻合度相對較好，采用的計算方法，材料模型、接觸設置等可應用于碎片超高速碰撞蜂窩夾層板的數值模擬與后續研究中。

經過模型驗證后，采用SPH-FE耦合的方法數值模擬直徑2 mm的球形彈丸以4.57 km/s對METOP上不帶隔熱層的蜂窩夾層板(前后面板厚度一致)超高速碰撞過程，仿真過程如圖4所示。大約0.4 μs前，球形彈丸撞擊前面板后發生破碎，前面板的一部分碎片在碰撞后也獲得了較大速度，與球形彈丸碎片混合在一起，形成了碎片云。約2.8 μs時，碎片云運動碰撞到了蜂窩芯子，由于蜂窩芯子的存在會阻礙碎片云徑向的擴散，碎片云被束縛在一個或多個蜂窩芯格內。蜂窩芯子受到碎片云的沖擊，產生極大的塑性變形，甚至蜂窩芯子被扭曲撕裂，蜂窩芯子的扭曲變形吸收了碎片云的部分動能，降低了碰撞后面板時碎片的數量和能量，從而削弱了碎片云對后面板的損傷。16.8 μs之后，碎片云的動能基本進入穩定狀態。

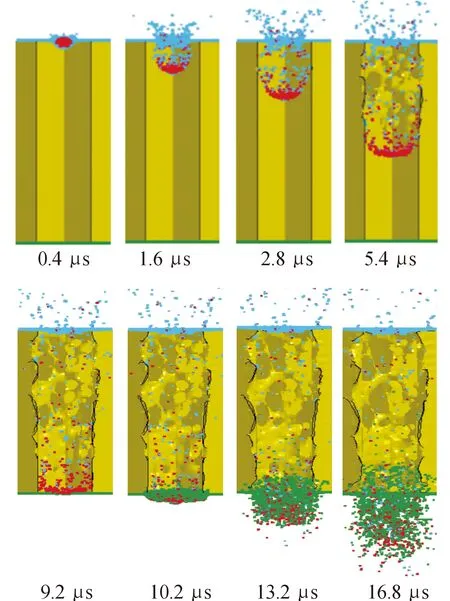
圖4 仿真彈丸超高速碰撞蜂窩夾層板過程

2 最優拉丁超立方試驗設計及數值模擬

2.1 最優拉丁超立方試驗設計

最優拉丁超立方設計(Optimal Latin hypercube design)改進了隨機拉丁超立方設計的均勻性，讓因子和響應的擬合更加精確真實，同時使所有的試驗點盡量均勻的分布在設計空間，具有非常好的空間填充性和均衡性。圖5顯示了拉丁超立方隨機生成的試驗分布與最優拉丁超立方生成的試驗點分布。

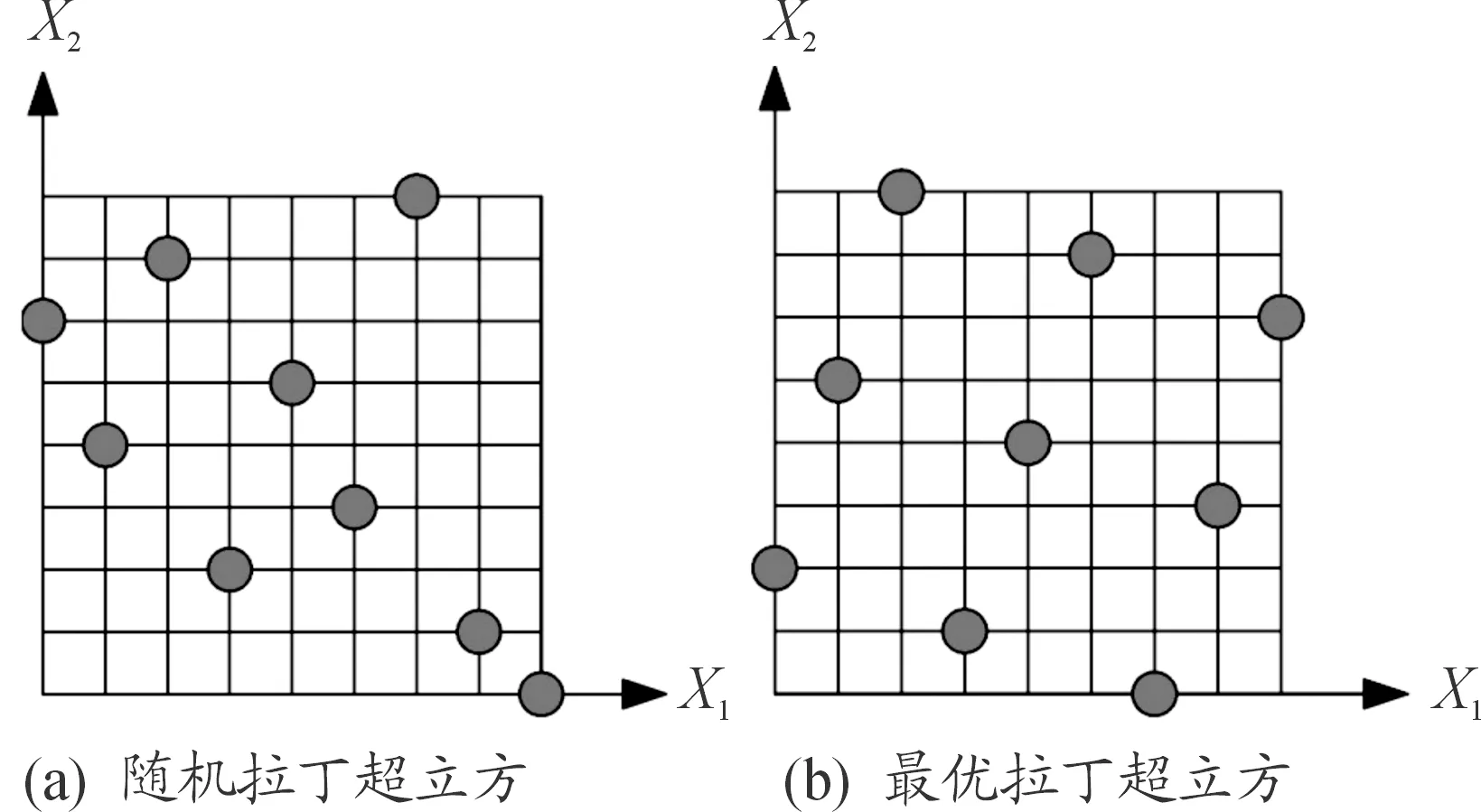
圖5 拉丁超立方隨機設計和最優設計的試驗點分布示意圖

2.2 試驗設計及仿真結果

在碎片超高速碰撞蜂窩夾層板時，本文主要考慮如何改變蜂窩夾層板的尺寸參數來提升蜂窩夾層板的防護能力。由于前后面板一般采用相同材料及相同厚度，選取蜂窩夾層板主要的4個尺寸參數：前面板厚度tf、單蜂窩芯格邊長lhc、蜂窩芯子高度S、蜂窩芯子壁厚thc作為優化參數，通過調研國內外蜂窩夾層板的規格與尺寸參數范圍，確定具體設計變量及其取值范圍如表4所示。

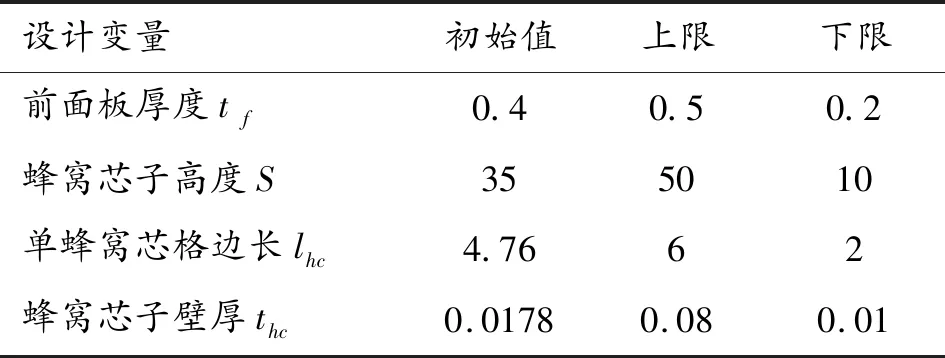
表4 蜂窩夾層板結構設計變量及取值范圍 mm

本算例涵蓋前面板厚度0.2～0.5 mm，蜂窩芯子的高度10～50 mm，單蜂窩芯格的邊長10～50 mm，單蜂窩芯格的邊長2～6 mm，蜂窩芯子的壁厚0.01～0.08 mm的組合情況，基于最優拉丁超立方法建立了25個樣本點構成的設計方案。在彈丸直徑2 mm與正入射速度4.57 km/s不變的情況下，對25個樣本點進行數值模擬，得到彈丸損失動能的數據，選取部分結果如表5所示。本文中的動能損失是球形彈丸形成碎片云的動能損失，通過LS-PREPOST后處理軟件得到初始彈丸動能與球形彈丸形成碎片云后的動能，計算兩者之間差值則為動能損失。仿真過程中對大變形的蜂窩芯子殼單元進行了單元刪除，最終碎片云的形成主要由后面板破碎形成的碎片云與彈丸破碎后形成的碎片云組成，彈丸的動能損失一定程度上能反映蜂窩芯子的吸能能力。

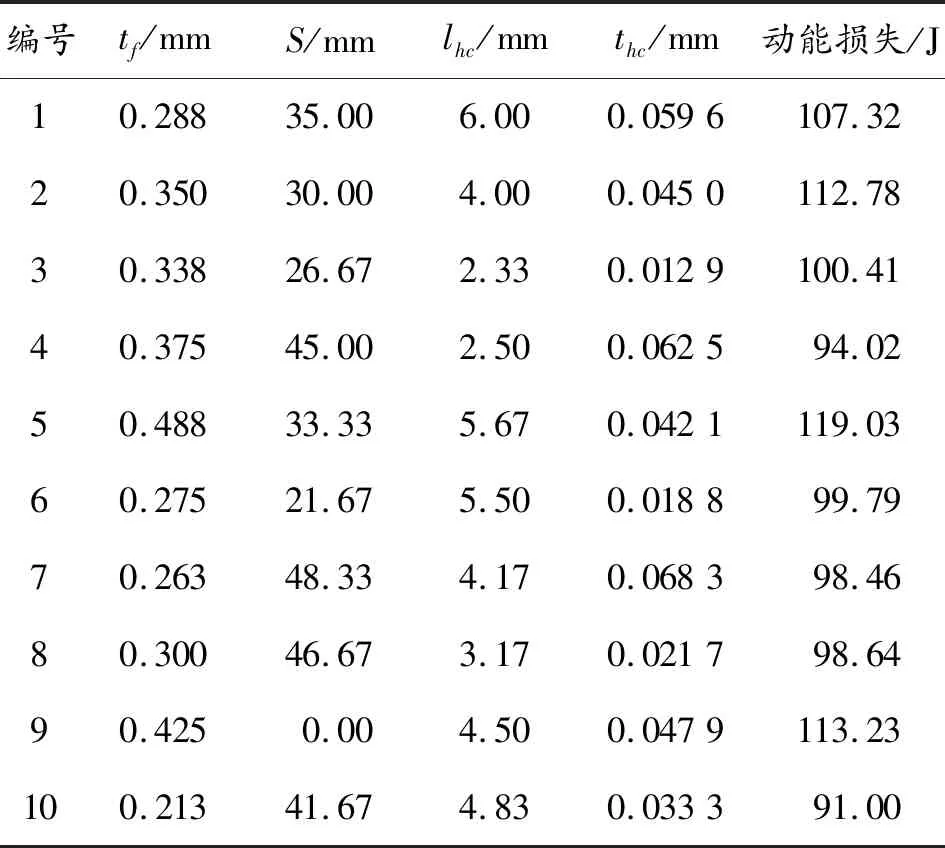
表5 最優拉丁超立方試驗設計及數值模擬值(部分)

3 基于Kriging方法的近似模型構建

Kriging方法又稱空間局部插值法，最早由南非地質學者Danie Krige提出，是一種以變異函數理論和結構分析為基礎，在有限區域內對區域化變量進行無偏最優估計的方法，也是地統計學的主要內容之一。當輸入變量數為4時，初始化克里格近似模型至少需要9個設計樣本點，上述最優拉丁方試驗設計方案中樣本數量為25，約為基本數量的278%，有利于提高模型的擬合精度。

(1)

式中：λi為待定加權系數。

克立格插值的關鍵就是求解權重系數λi，其必須滿足兩個條件：

1) 無偏估計。

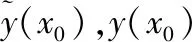
(2)

即

(3)

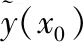
(4)

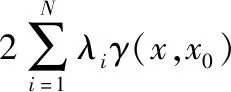
(5)

式中：γ(xi,xj)表示以xi和xj兩點間的距離作為間距h時參數的半方差值，γ(xi,x0)則是以xi和x0兩點之間的距離作為間距h時參數的半方差值。

建立Kriging模型后，在優化前為了保證該模型精度足夠高對近似模型采用誤差平方R2(R-Square) 進行檢驗。R2可用來衡量近似模型與樣本點項符合的程度，其大小在0～1，R2越趨近于1，越表示近似模型具有高可信度。本文中R2的值為0.945 85，大于設定的可接受水平0.9。采用均方根誤差RMSE(Root Mean Square Error) 進行檢驗時，RMS值為0.071 5，低于可接受水平0.2。采用相對平均絕對誤差RAAE(Relative Average Absolute Error) 進行檢驗時，RAAE值為0.063 26，低于可接受水平0.2。采用相對最絕對誤差RMAE(Relative Maximum Absolute Error) 進行檢驗時，RMAE值為0.097 92，低于可接受水平0.3。因此，該模型可信度較高。

憲法意識不會自發產生，必須通過專門的培養才得以形成。提升憲法意識是學習和宣傳憲法，深化法制教育，培育卓越法治人才的內在要求。為提升大學生的憲法意識，引導大學生樹立社會主義法治理念，可以從以下三個方面提升大學生憲法意識。

在對近似模型進行誤差分析的同時，從優化設計域內隨機選擇兩組盡量遠離樣本點的設計參數建模進行數值模擬，近似模型預測值與仿真值如表6所示。球形彈丸動能損失預測值與仿真值的誤差小于3%，在可接受范圍之內。

表6 Kriging模型隨機非樣本點檢驗值

4 基于AMGA算法的蜂窩夾層板結構優化

4.1 AMGA算法

存檔微遺傳算法(Archive-Based Micro Genetic Algorithm ，AMGA)在進化過程之外設立一個存檔，用于保存進化過程中的非支配個體及相應的多目標函數值。對每個子目標分別進行處理，所保存的可行非支配設計即組成最優的Pareto前沿。這種算法適用于高度非線性、不連續或非凸及高度約束的搜索空間，方法如下：

4.2 優化問題描述

在滿足超高速碰撞防護性能要求的同時，希望蜂窩夾層板結構的面密度越小越好。蜂窩夾層板結構面密度由前后面板密度、蜂窩芯層密度及粘結層決定，為簡化計算，忽略粘結層的質量，因此，正六邊形蜂窩夾層板的面密度可表示為：

ρ=2tfρf+Sρhc

(5)

(6)

(7)

式中：ρf為前后面板材料的密度；ρhc為蜂窩材料的密度；ρ0為蜂窩基體材料的密度；ρ為蜂窩夾層結構的面密度。

設計變量：

(8)

目標函數：

(9)

(10)

約束條件：

(11)

4.3 優化結果及討論

蜂窩夾層板的結構參數通過AMGA算法進行優化，優化計算獲取的4組候選分析值如表7所示。

對比初始模型的數據與優化后的數據可以看出，通過多目標優化，蜂窩夾層板的吸能能力得到了提升，面密度減小。其中，方案1的動能損失最小，方案2、方案3雖然蜂窩夾層板吸能能力得到提升，略高于方案4，但蜂窩夾層板的面密度沒有得到明顯減小。最終選取方案4為最終方案。

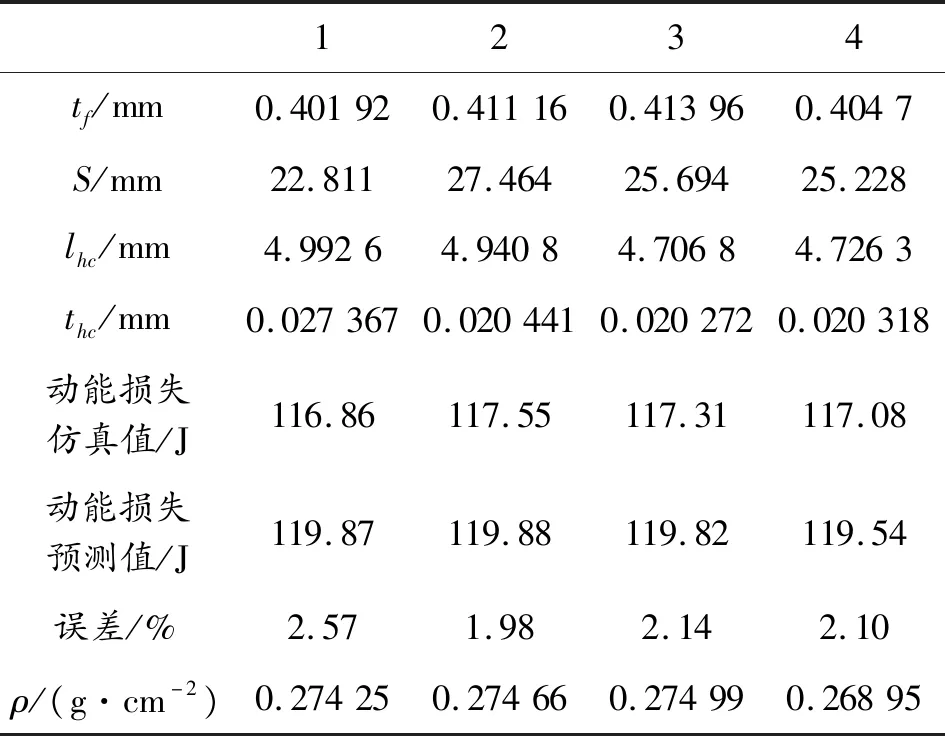
表7 多目標優化值

圖6 優化前后彈丸動能變化對比

與初始設計相比，優化后占蜂窩夾層板質量比例較大的前后面板厚度略有增加，蜂窩芯子的間距大幅減小，而蜂窩胞壁的厚度略有增加以提升蜂窩夾層板整體的吸能能力。由于減少了蜂窩芯子間距，優化后碎片云更快碰撞到后面板而動能大幅減小，導致了優化前后動能損失的時間節點的差異。彈丸損失的動能與蜂窩夾層板面密度結果表明，采用優化后的結構得到的球形彈丸動能損失率更大，提升了約1.76%。蜂窩夾層板結構的面密度由初始模型的0.275 6 g/cm2減少為0.268 95 g/cm2。

5 結論

1) 通過最優拉丁超立方法對蜂窩夾層板的4個尺寸參數進行了試驗設計，并利用LS-DYNA軟件中SPH-FE方法對25個樣本點進行了數值模擬。構建蜂窩夾層板結構多目標設計的Kriging近似模型，經隨機點驗證表明該模型誤差在可接受范圍內。

2) 基于AMGA算法進行迭代計算，通過對優化前后的數值模擬結果進行對比，發現優化后球形彈丸動能損失增加約1.76%，蜂窩夾層板面密度減少了0.006 65 g/cm2，提高了蜂窩夾層板結構的吸能能力并滿足了輕量化要求。

3) 優化后的參數為超高速碰撞下蜂窩夾層板結構的設計提供了理論參考，減少了計算量，提高了優化效率。