裝藥密度對炸藥JWL狀態方程的影響

栗保華，暢 博，張立建，呂永柱，谷鴻平

(西安近代化學研究所，西安 710065)

爆轟產物狀態方程是描述炸藥爆轟CJ狀態之后的爆轟產物系統中各物理量的關系式，是研究計算爆炸力學問題的基礎。其中JWL狀態方程由于能夠比較精確地描述炸藥爆轟產物的膨脹驅動過程，目前在武器設計、工程爆破、爆炸加工等領域得到了廣泛應用的很多大型有限元軟件，如LS-DYNA、ABAQUS、MSC．Dytran、AUTODYN等都在炸藥材料模型中包含了JWL狀態方程。

JWL狀態方程是由Lee于1965年在Jones和Wilkins工作的基礎上提出的，該方程的未知參數需要通過炸藥的圓筒試驗及二維流體動力學程序來確定。圓筒試驗是使炸藥在銅管中爆炸，利用高速掃描相機記錄下管壁在爆轟產物驅動下的膨脹過程，得出圓筒半徑變化曲線，然后采用含有JWL狀態方程的二維流體動力學程序來對圓筒試驗進行數值模擬，不斷修改JWL狀態方程參數，直至數值模擬結果與圓筒試驗結果相符合，從而確定最終的JWL狀態方程參數。

由于確定JWL狀態方程參數過程中的圓筒試驗所用藥柱尺寸小、形狀規則，而實際戰斗部裝藥尺寸較大、外形復雜，戰斗部實際裝藥密度一般要低于圓筒試驗的裝藥密度，因此圓筒試驗通常給出的是炸藥在一種較高裝藥密度下的JWL狀態方程參數。在破片戰斗部威力數值仿真中，需要用到同種炸藥在其他密度下的JWL狀態方程參數時，一般認為JWL狀態方程的A、B、R1、R2、ω和E0這6個參數是不隨裝藥密度變化的。但通過對文獻中PETN和HNS兩種炸藥在不同密度下的JWL狀態方程研究發現，JWL狀態方程的參數明顯與裝藥密度有關，裝藥密度對炸藥的驅動能力影響較大。因此，研究炸藥在不同密度下的JWL狀態方程參數，對提高破片戰斗部威力數值仿真的準確度具有重要意義。

本研究通過理論分析及與兩種炸藥JWL狀態方程參數的對比，建立了不同裝藥密度下的JWL狀態方程參數計算方法，可快速準確地確定出炸藥在任意密度下的JWL狀態方程參數。

1 目前的研究現狀

目前國內關于裝藥密度對JWL狀態方程參數的影響研究很少，炸藥在不同密度下的JWL狀態方程參數僅極少數炸藥可在公開文獻中查到，這大大影響了JWL狀態方程在實際應用中的精度。國內也有人通過基于理論模型建立的BKW[1]、γ率狀態方程[2]、VLW[3-4]、KHT[5]等狀態方程的計算結果擬合得到炸藥的JWL狀態方程的參數，但均需要知道炸藥的詳細配方及相關參數才可得出較為可信的結果，而工程上很多新炸藥的配方和一些參數都是未知的，因此很難通過此方法獲得炸藥的JWL狀態方程參數。下面對炸藥在不同裝藥密度下的JWL狀態方程參數進行理論分析和研究。

2 不同裝藥密度下的炸藥JWL狀態方程

炸藥爆轟產物的JWL狀態方程形式如下：

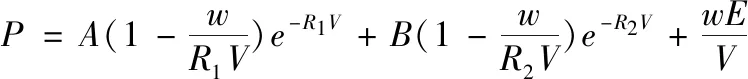
(1)

式中：A、B、R1、R2、ω為炸藥的JWL狀態方程參數。

在CJ點處，JWL狀態方程形式如下：

(2)

式中:PCJ為炸藥的爆壓；VCJ為炸藥的爆容；E0為炸藥的初始比內能。

從式(2)可以看出，JWL狀態方程的A、B、R1、R2、ω5個參數需要知道炸藥的爆壓、爆容和初始比內能才能確定，而這3個參數均與炸藥的裝藥密度有關。

1968年，康姆萊特(kamlet)等提出了計算CHNO型炸藥爆壓和爆速的半經驗半理論計算公式，稱為康姆萊特公式[6]，它適用于裝藥密度大于1 g/cm3的情況。其形式簡單，計算精度較高，具體形式如下：

(3)

PCJ=1.558φρ2

(4)

(5)

式中：φ為與炸藥的組分有關的參數；ρ為炸藥的裝藥密度。

若已知某裝藥密度ρ0時的爆速D和爆壓PCJ，則由式(4)可推導出炸藥在任意密度下的爆壓如下：

(6)

由式(5)可推導出炸藥在任意密度下的爆速如下：

(7)

將式(2)代入式(6)可得：

(8)

將式(8)與式(2)對比，可以得到炸藥在任意裝藥密度下的爆轟產物JWL狀態方程參數如下：

(9)

其余3個參數R1、R2、ω保持不變。

3 結果分析與對比

采用上述模型計算了PETN和HNS兩種炸藥在不同密度下的JWL狀態方程參數，并根據文獻[7]和文獻[8]中兩種炸藥在不同密度下JWL狀態方程參數，制作了對爆轟產物膨脹的壓力-體積曲線。PETN炸藥JWL狀態方程參數的文獻值與計算值對應的爆轟產物膨脹壓力-體積曲線對比如圖1所示。HNS炸藥JWL狀態方程參數的文獻值與計算值對應的爆轟產物膨脹壓力-體積曲線如圖2所示。

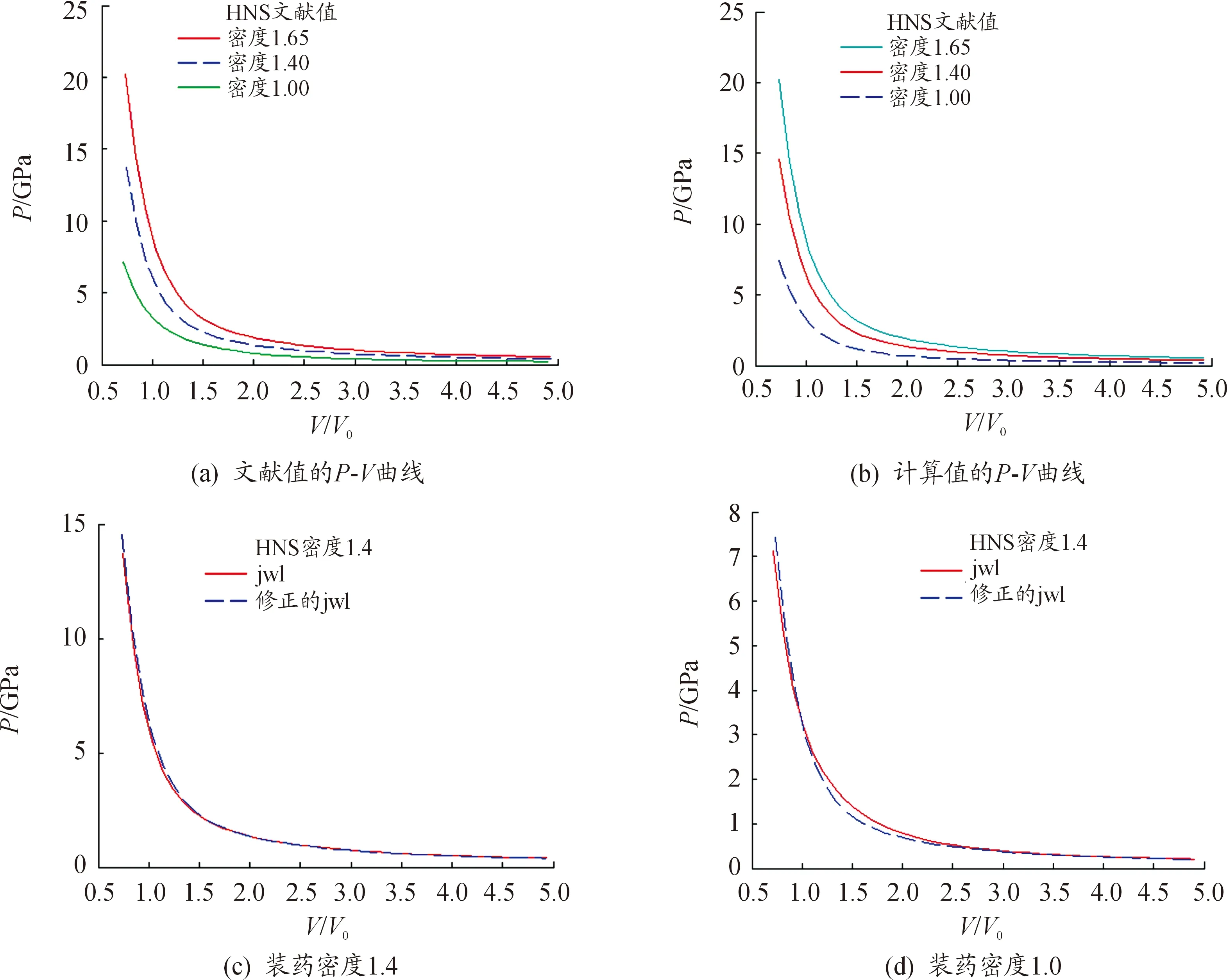
圖2 HNS文獻值與計算值的P-V曲線

從圖1(a)～1(b)和圖2(a)～2(b)可以看出，當裝藥密度降低時，爆轟產物在高壓段的壓力曲線明顯下降，若在數值仿真時對低密度裝藥采用高密度下測得的JWL狀態方程參數，將給仿真結果帶來較大的計算誤差，尤其是當圓筒試驗的裝藥密度與實際裝藥密度相差較大時，應當對JWL狀態方程參數進行相應的修正。

從圖1(c)～1(d)和圖2(c)～2(d)可以看出，PETN和HNS兩種炸藥在裝藥密度大于1 g/cm3時，爆轟產物膨脹P-V曲線計算值與文獻值在高壓段和低壓段均吻合較好，比較準確地反映了炸藥在不同密度下爆轟產物膨脹規律,因此將來可以在戰斗部威力數值仿真中應用該模型對某些炸藥的JWL狀態方程的參數進行修正，以提高數值仿真結果的精度。

PETN和HNS在不同密度下的JWL狀態方程參數計算值與文獻值如表1與表2所示。

表1 PETN炸藥不同密度下的JWL狀態方程參數

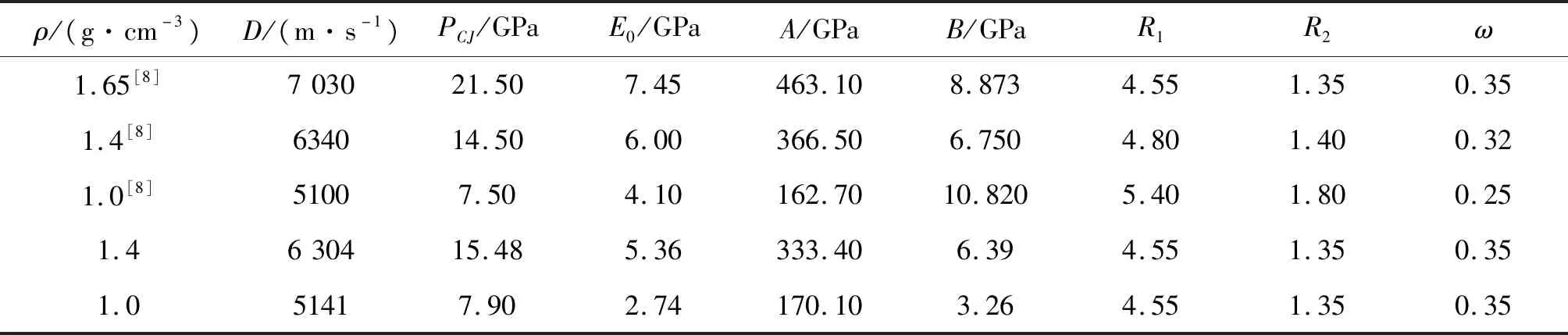
表2 HNS炸藥不同密度下的JWL狀態方程參數

由表1和表2可以看出，2種炸藥不同密度下的JWL狀態方程參數計算值與文獻值差異較大，但兩種炸藥不同密度下的爆轟產物膨脹P-V曲線計算值與文獻值吻合較好，這說明JWL狀態方程的參數在數學上存在不唯一解。

例如某破片戰斗部裝填DNTF基炸藥，通過圓筒試驗結果擬合得到DNTF基炸藥的JWL狀態方程，并測得裝藥密度為1.875 g/cm3，爆速為8 649 m/s，但實際由于裝藥條件限制，戰斗部的裝藥密度僅為1.77 g/cm3。根據該炸藥圓筒試驗的JWL狀態方程參數及參數，由式(6)和式(7)可計算出實際裝藥密度下的參數，分別用兩套參數采用LS-DYNA進行戰斗部爆炸過程的數值仿真，破片初速仿真結果如下：

從圖3可以看出，原始參數和修正后參數的破片最大速度分別為2 390.3 m/s和2 174.4 m/s，而試驗測得破片的最大初速為2 120 m/s。由此可見，修正后的參數仿真得到的戰斗部破片速度均與試驗結果吻合更好。

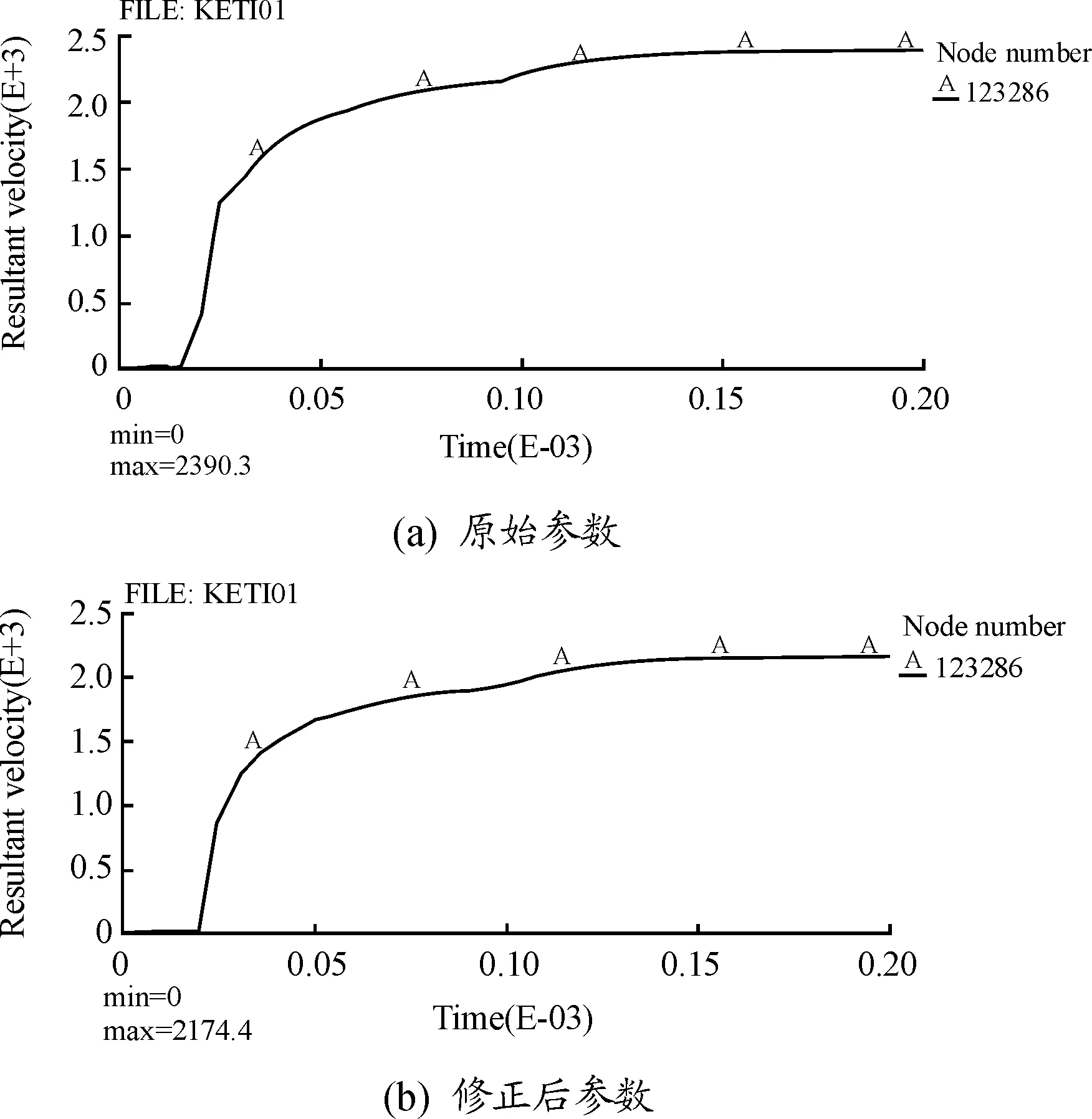
圖3 戰斗部中心位置破片速度的仿真曲線

4 結論

1) 當裝藥密度降低時，爆轟產物在高壓段的壓力會明顯下降，若在數值仿真時對低密度裝藥采用高密度下測得的JWL狀態方程參數將給仿真結果帶來較大的計算誤差，尤其是當圓筒試驗的裝藥密度與實際裝藥密度相差較大時，應當對JWL狀態方程參數進行修正。

2) PETN和HNS兩種炸藥在裝藥密度大于1 g/cm3時，爆轟產物膨脹P-V曲線計算值與文獻值在高壓段和低壓段均吻合較好，比較準確地反映了炸藥在不同密度下爆轟產物膨脹規律,因此將來可以在戰斗部威力數值仿真中應用該模型對某些炸藥的JWL狀態方程的參數進行修正，以提高數值仿真結果的精度。

3) 兩種炸藥不同密度下的JWL狀態方程參數計算值與文獻值差異較大，但兩種炸藥不同密度下的爆轟產物膨脹P-V曲線計算值與文獻值吻合較好，這說明JWL狀態方程的參數在數學上存在不唯一解。

4) 通過用圓筒試驗得到的DNTF基炸藥JWL狀態方程參數及本模型修正后的參數，分別進行數值仿真并與試驗對比，修正后的參數仿真得到的戰斗部破片速度與試驗結果吻合更好。

因此，本研究的計算模型可以較為準確地預測炸藥在不同裝藥密度下的JWL狀態方程參數和爆轟產物膨脹規律，能夠用于破片戰斗部威力數值仿真中提高仿真結果的準確度，為未來的精密戰斗部設計提供理論支撐。限于公開文獻中關于炸藥在不同裝藥密度下的JWL狀態方程參數較少，該模型的準確性還有待更多的試驗數據驗證和完善。