從一題多解探析三重積分的計算方法

趙金虎

（阜陽師范大學 數學與統計學院，安徽 阜陽，230637）

1 引言

三重積分是高等數學中的一個重點，也是很多學生考研復習中的一個難點，因此，三重積分的計算成了近年來高等數學教學研究的熱點問題。賈建文探討了直角坐標系下三重積分的計算技巧，用不等式組的方法列出了三重積分化為累次積分的公式。[1]鄭華盛介紹了三重積分交換積分次序的普適方法，并通過實例和應用驗證了有效性。[2]蔣銀山討論了三重積分的幾種計算方法，包括先一后二法、先二后一法、柱面坐標法、球面坐標法、積分區域的對稱性與被積函數的奇偶性等。[3]呂中學通過實例檢驗了各種類型的空間體中三重積分的計算方法。[4]孟飛將二重積分在極坐標系下積分順序的交換方法推廣到了三重積分的球面坐標計算中。[5]井晨睿等對比研究了不同坐標系下三重積分的計算方法，根據被積函數以及積分區域的特點，提出了選取坐標系的方法[6]。曹秀梅、吳自庫總結和推廣了三重積分中“先二后一”的計算方法，通過例題拓展了計算技巧。[7]趙小艷和李繼成通過例子詳細說明了如何選取適當的方法計算三重積分，對于如何確定不同坐標系下的積分上下限進行了區分和總結。[8]劉菊青分析了三重積分在直角坐標系下的截面法，從理論上解決了三重積分計算的抽象性和合理性。[9]方汶銘指出變量置換是三重積分在柱（球）面坐標系中計算的本質，并討論了不同坐標系中若干變形的處理方法。[10]

學生很難掌握三重積分的各種計算方法，主要原因在于積分區域是三維的，而學生的空間想象能力有限，導致三重積分轉化為累次積分的時候，學生很難確定各個積分變量的積分限，這是困擾學生的一個主要障礙。鑒于上述背景，本文從可視化的角度，分析了同一道三重積分的四種計算方法，探討了不同方法中分步驟選取各個積分變量上下限的有效策略，使學生能夠全面地認識和掌握三重積分的各種計算方法。請看本文的題目其中V由曲面x2+y2=z2與z=1所圍成[11]，如圖1所示。

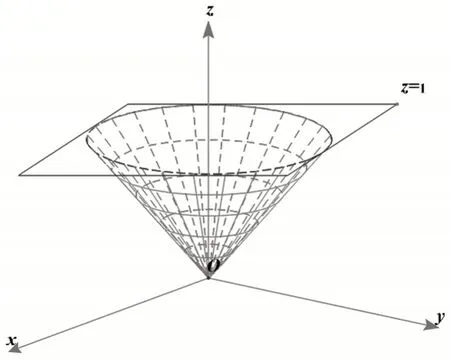
圖1 積分區域示意

2 計算三重積分

2.1 截面法

截面法又稱作“先二后一”法，首先把積分區域視為介于兩個平行平面z=e和z=h之間的立體[12]，也就是考慮變量z能夠取得的最大值與最小值，在本題中z∈[]0,1；然后用垂直于z軸的平面截積分區域，設所得截面為Dz（如圖2所示），也就是把曲面方程中的z看作常數，在本題中此時將三重積分轉化為先對變量x、y在平面區域Dz上的含參變量的二重積分，再對z∈[0,1]求定積分的形式。由于截面為圓域，平面區域Dz上的二重積分結合極坐標變換完成。用截面法解決本題的完整過程如下：

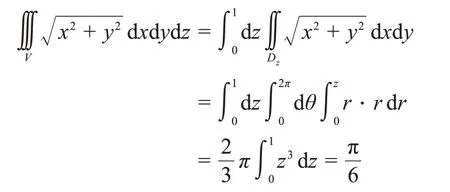
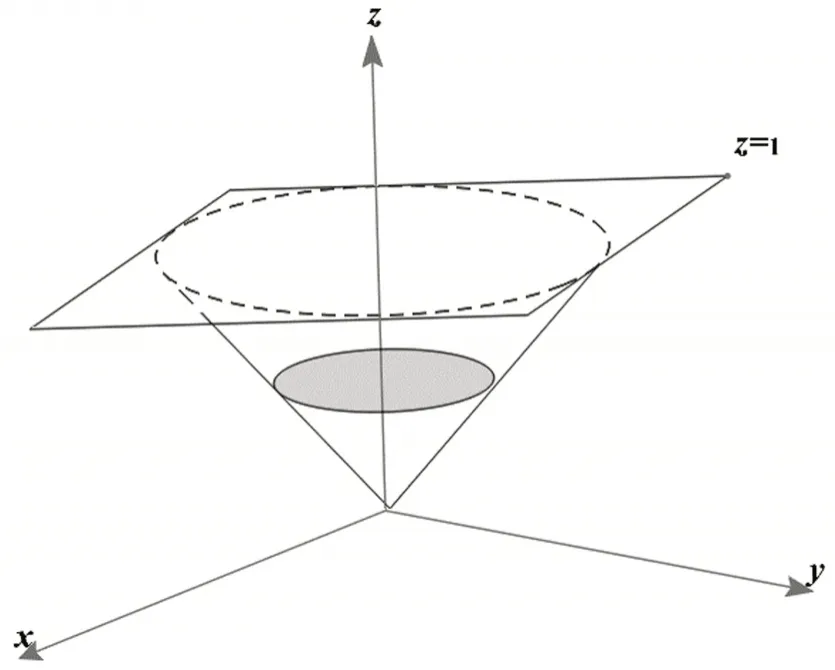
圖2 .截面示意

2.2 投影法

投影法又被稱作“先一后二”法，首先把積分區域視為柱體的一部分，投影區域D為類比的柱體底面，也就是將積分區域中垂直于z軸的最大平面區域作為柱體底面，在本題中圓錐面x2+y2=z2與平面z=1相交得到的圓為x2+y2=1，該圓域形成了投影區域D={(x,y)|x2+y2≤1}，如圖3所示。然后確定變量z介于上下曲面z=z1(x,y)和z=z2(x,y)之間，在本題中z介于圓錐面與平面z=1之間。最后，三重積分轉化為先對z的含參量積分，再形成對x、y的二重積分形式。同理，由于投影區域為圓域，關于x、y的二重積分可結合極坐標變換完成。用投影法解決本題的完整過程如下：

圖3 投影示意

2.3 柱面坐標變換

柱坐標變換是計算三重積分的換元法中兩個最常用的變換之一，當積分區域或被積函數含有x2+y2或x2+y2+z2時，可考慮使用柱面坐標變換。構成柱面坐標的三個坐標中，“r=常數”表示以z軸為中心軸的圓柱面，“φ=常數”表示以z軸為邊緣的半平面，“z=常數”表示平行于坐標面xOy的平面。柱面坐標變換可以認為是投影加極坐標變換的過程，通常是先找出積分區域V在xOy平面上的投影區域D，然后確定變量z介于曲面z=z1(x,y)和z=z2(x,y)之間，并轉化為r和φ來表示，在本題中投影區域D={(r,φ)|0≤r≤1,0≤φ≤2π}，z介 于z=與平面z=1之間，如圖4所示。所以，利用柱面坐標變換解決本題的完整過程如下：

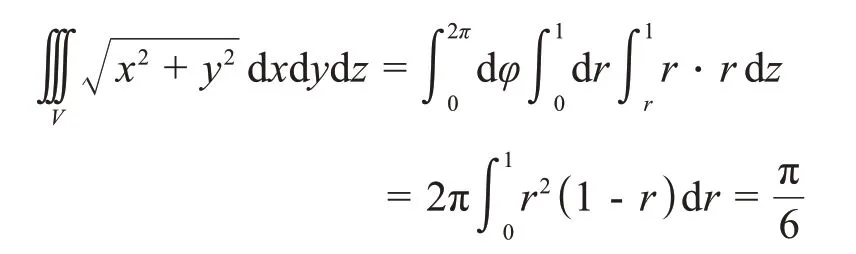
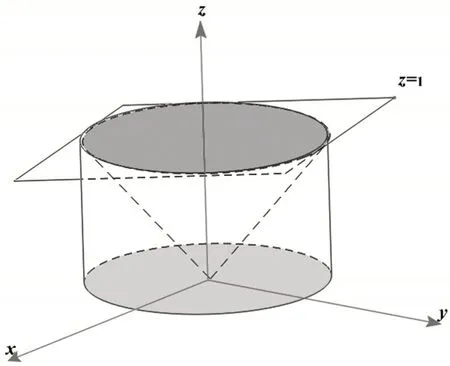
圖4 柱面坐標示意

2.4 球面坐標變換

當積分區域或被積函數含有x2+y2+z2或x2+y2時，可考慮使用球面坐標變換。構成球面坐標的三個坐標中，“r=常數”表示以原點為中心的球面，“φ=常數”表示以原點為頂點，以z軸為對稱軸的圓錐面，“θ=常數”表示以z軸為邊緣的半平面。使用球面坐標變換時，需要把積分區域中直角坐標系下的方程都轉化為球面坐標系下新的變量來表示，以此來確定球面坐標變量的積分限，沒有限制條件的變量選取默認的范圍，比如θ∈[ 0,2π]。在本題中，圓錐面x2+y2=z2轉化為了cos 2φ=0，即此為與z軸夾角的上限；平面z=1轉化為rcosφ=1，即此為球面半徑的上限，表示積分區域限制在平面z=1以下，并不能超出這個平面到更外側r=1的球面上（如圖5所示）。利用球面坐標變換解決本題的完整過程如下：

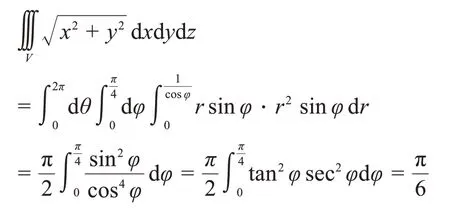
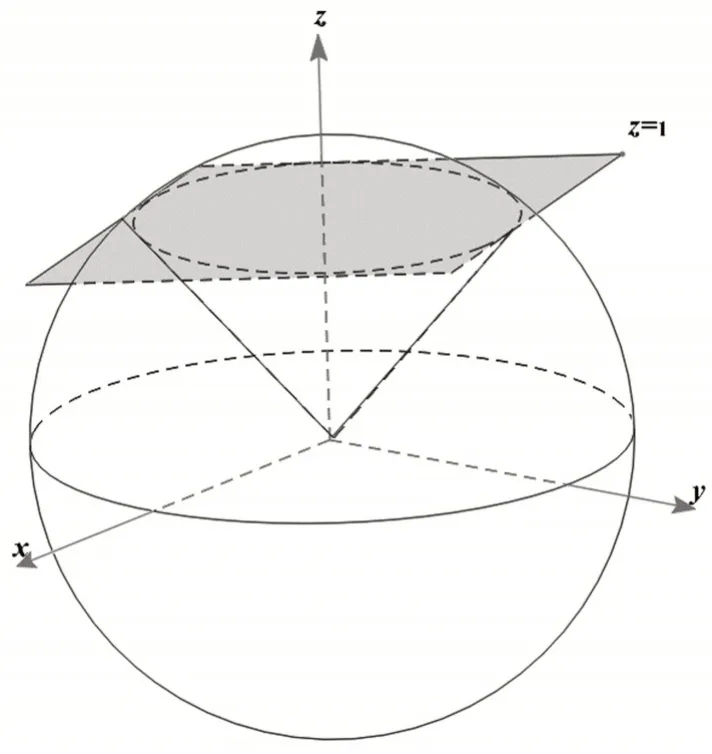
圖5 球面坐標示意

3 結語

在學習三重積分的計算時，學生遇到的最大問題是難以獲得各個積分變量的積分限。本文利用同一道三重積分的計算題，針對四種不同的計算方法，分析了如何快捷地把三重積分轉化為累次積分。學生應當加強空間想象力的訓練，加深對此類問題的理解，并做到觸類旁通，舉一反三，這樣才能熟練掌握三重積分的各種計算方法。