基于高階思維視域下的初中數(shù)學教學設計

鐘凱丹 楊靈娥

【摘要】? 本文結合數(shù)學學科的特色，提出培養(yǎng)學生高階思維能力的教學設計要關注的六大方面：情境、支架、表達反饋、信息技術、跨學科融合、反思意識，并以問題設計為重點，對人教版八年級上冊“等腰三角形”第一課時進行了教學設計，試圖為在數(shù)學課堂上培養(yǎng)學生的高階思維能力提供一些啟示.

【關鍵詞】? 高階思維能力;初中數(shù)學;等腰三角形;教學設計

布盧姆在《教育目標分類學：認知領域》中，將教學目標劃分為六大類——識記、理解、應用、分析、綜合及評價.后人在其分類的基礎上，把分析、綜合、評價、創(chuàng)造定義為高階思維，并界定其核心能力是創(chuàng)新能力、決策能力、問題解決能力和批判思維能力.高階思維的發(fā)展是需要高階學習為載體的，而高階學習是一種問題求解的學習活動.

一、培養(yǎng)學生高階思維能力的教學設計

綜合學者的論述，并結合數(shù)學學科的特色，我們在進行高階思維教學設計時應關注以下六個方面.

1.創(chuàng)設情境，分發(fā)任務

創(chuàng)設真實情境的目的在于讓學生在與真實世界接軌的學習環(huán)境中感受、體驗.如在學習數(shù)據(jù)分析時，教師可讓學生收集疫情期間的相關數(shù)據(jù)，并對數(shù)據(jù)進行分析和統(tǒng)計，從而推斷出疫情發(fā)展的趨勢，提高數(shù)學的應用性.教師還可創(chuàng)設數(shù)學史的情境，如在教學“用字母表示數(shù)”時，可滲透代數(shù)的發(fā)展，從古巴比倫人的文字敘述到丟番圖用字母縮寫表示數(shù)量間的關系，再到韋達用字母當作符號表示數(shù)，通過這三大階段既可以展示數(shù)學文化的魅力，讓學生獲取探究的樂趣，又可以讓學生認識到用字母表示數(shù)是人類認識的一次飛躍.不管是哪種情境的設計，設置的情境問題要有一定的難度，進而把高層次的分析、評價、綜合、創(chuàng)造運用到求解問題的過程中.

2.以學生為主體，提供支架

支架式教學是把有難度、復雜的學習任務在學生的發(fā)展區(qū)內(nèi)加以分塊，

讓學生一步步消化吸收并引向深入.因此，教師可以通過設置任務單為學生提供支架，把學習主動權還給學生，讓學生在探索中主動進行知識的建構，對信息進行篩選、加工、處理、創(chuàng)造，從而在“做”中獲得提高高階思維能力的機會，從而提升自身的思維能力及品質(zhì).

3.雙向表達反饋

語言智力是加德納多元智能理論中的一項，是指學生對知識的闡述能夠從另一個方面反映出學生對這個知識點的掌握程度.但是，大部分學生只關注自我分享與表現(xiàn)，因此，教師要引導學生從他人的觀念、建議中提煉出他人在問題解決中的優(yōu)點及不足，并能夠結合他人的方案提出可供參考的建議，形成雙向表達反饋的模式，發(fā)展學生的批判性思維.

4.妙用信息技術

信息技術是問題解決過程中的輔助性工具，弄清楚它的定位，能幫助學生更好地構建、理解知識，促進高階思維的發(fā)展.對于數(shù)學學科來講，要提高教學質(zhì)量，教師就要掌握好信息技術的使用，如幾何畫板、GeoGebra，這都是非常流行的數(shù)學教學平臺，是功能齊全且強大，是數(shù)學教師進行教學、研究的重要工具.它們可以使問題可視化，透過現(xiàn)象看本質(zhì)，讓學生更好地理解知識，促進學生幾何直觀、數(shù)學抽象等核心素養(yǎng)的形成.

5.注重跨學科融合

一個問題的解決過程中往往涉及多個學科的知識，跨學科知識的融合可以真正實現(xiàn)思維的碰撞與激發(fā)，大大提高學生的興趣，幫助學生把所學的知識融會貫通，提高相關的學科素養(yǎng).如在教學“直線與圓的位置關系”時，教師可以通過蘇軾的詩“大漠孤煙直，長河落日圓”給學生清晰地描繪地平線與太陽的位置關系，從而抽象出直線與圓的位置關系.

6.培養(yǎng)反思意識

心理學認為，反思意識與反思行為是學習者對自身數(shù)學認知過程的反省、監(jiān)控.教師在課堂上要做好總結工作，引導學生對知識、數(shù)學思想方法進行梳理歸納，特別要對數(shù)學思想方法進行提煉.立足數(shù)學思想方法進行教學，能促進學生核心素養(yǎng)的形成，使其在遇到新問題的時候學會遷移，學會思考，從而達到不用“教”的教學效果.

二、案例分析

在教學中如何進行問題的設計呢？B. Dodge認為，教學? 中設計的問題要具有下列特征，才有助于高階思維能力的發(fā)展.

①比較、鑒別、闡明實物之間的類似之處和不同之處;②根據(jù)事物的屬性和特征將它們分類;③通過觀察和分析，歸納出一般化的原理;④通過給定的原理和法則，推導出未知的結果;⑤分析錯誤，即找出并闡明自己和他人思維中的錯誤;⑥找出支持的論據(jù)，即對每一個觀點和看法都要給出支持的論據(jù);⑦概括，即找出龐雜的信息下隱藏的規(guī)律和模式;⑧提出觀點，即能夠確定并闡明自己對問題的看法.

下面以人教版八年級上冊“等腰三角形”一課為例，圍繞第一部分的六大方面設計以高階學習為支撐的教學活動.

1.教材分析

“等腰三角形”一課是學生學習軸對稱知識基礎上的進一步研究.等腰三角形是一種特殊的三角形，它除了具備一般三角形的所有性質(zhì)外，還有許多特殊的性質(zhì)，也正是有了這些特殊的性質(zhì)，等腰三角形比一般三角形的應用更廣泛.“等腰三角形”一課學習的內(nèi)容主要有2個，即等腰三角形的兩個性質(zhì)——等邊對等角、三線合一，這兩個性質(zhì)是幾何中證明線段相等和角相等的重要依據(jù).

2.學情分析

學生已初步掌握了軸對稱、三角形等相關知識，這為順利完成這節(jié)課的教學任務打下了基礎.但是，由于經(jīng)驗的不足，學生在添加輔助線證明等腰三角形性質(zhì)時具有一定的困難.

3.教學內(nèi)容二度創(chuàng)新

根據(jù)對教材內(nèi)容的分析，結合課程標準要求——了解等腰三角形的概念，探索并證明等腰三角形的性質(zhì)定理：等腰三角形的兩底角相等，底邊上的高線、中線及頂角平分線重合，并基于高階思維，筆者對本節(jié)課的教學內(nèi)容進行了如下創(chuàng)新.

4.教學目標

（1）知識技能：探索并證明等腰三角形;綜合應用等腰三角形的性質(zhì).

（2）過程與方法：在問題的解決過程中經(jīng)歷觀察、猜想、證明的思維過程.

（3）情感、態(tài)度與價值觀：在交流、質(zhì)疑、評價中形成敢于探索、勇于創(chuàng)新的精神.

5.教學重難點

探索并證明等腰三角形的性質(zhì)，即等腰三角形的兩底角相等，底邊上的高線、中線及頂角平分線重合.

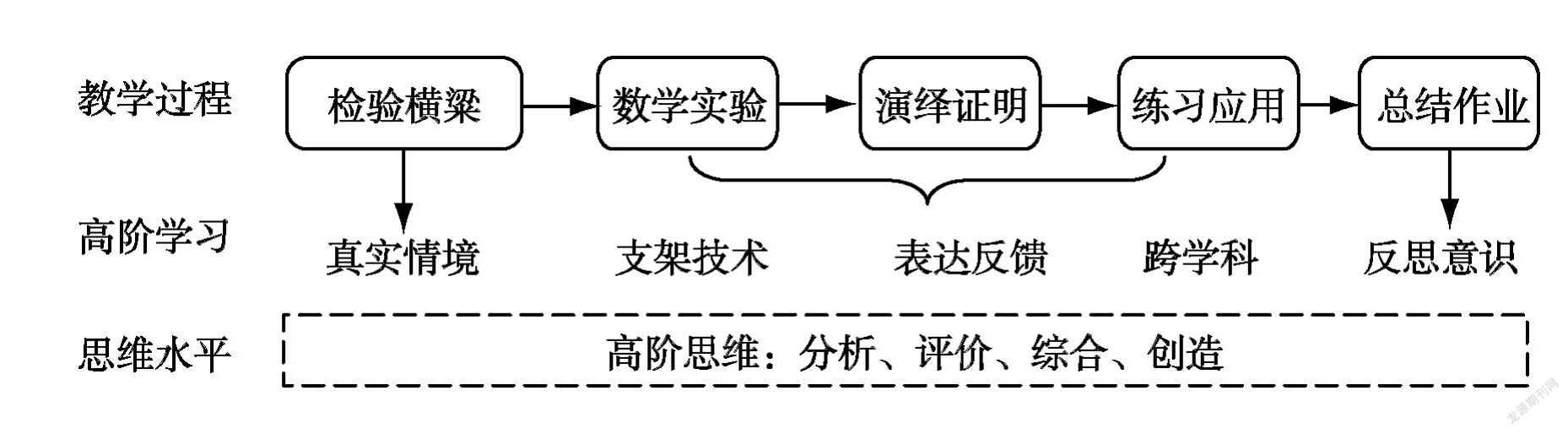
6.教學設計過程

（1）問題情境導入

在真實的生活中，我們常見到木工師傅用三角形測平架檢測房屋的橫梁是否保持水平狀態(tài).為了重現(xiàn)生活情景，筆者在等腰直角三角尺的斜邊中點掛一根繩子，繩的另一端掛一個鉛錘，測量一下教室黑板的下邊是否水平，并讓學生猜想這其中的奧秘.

設計意圖：教師通過創(chuàng)設真實情境問題，引導學生將對課堂產(chǎn)生的直接興趣轉為進一步的探究，這是培養(yǎng)學生高階思維能力的前提.

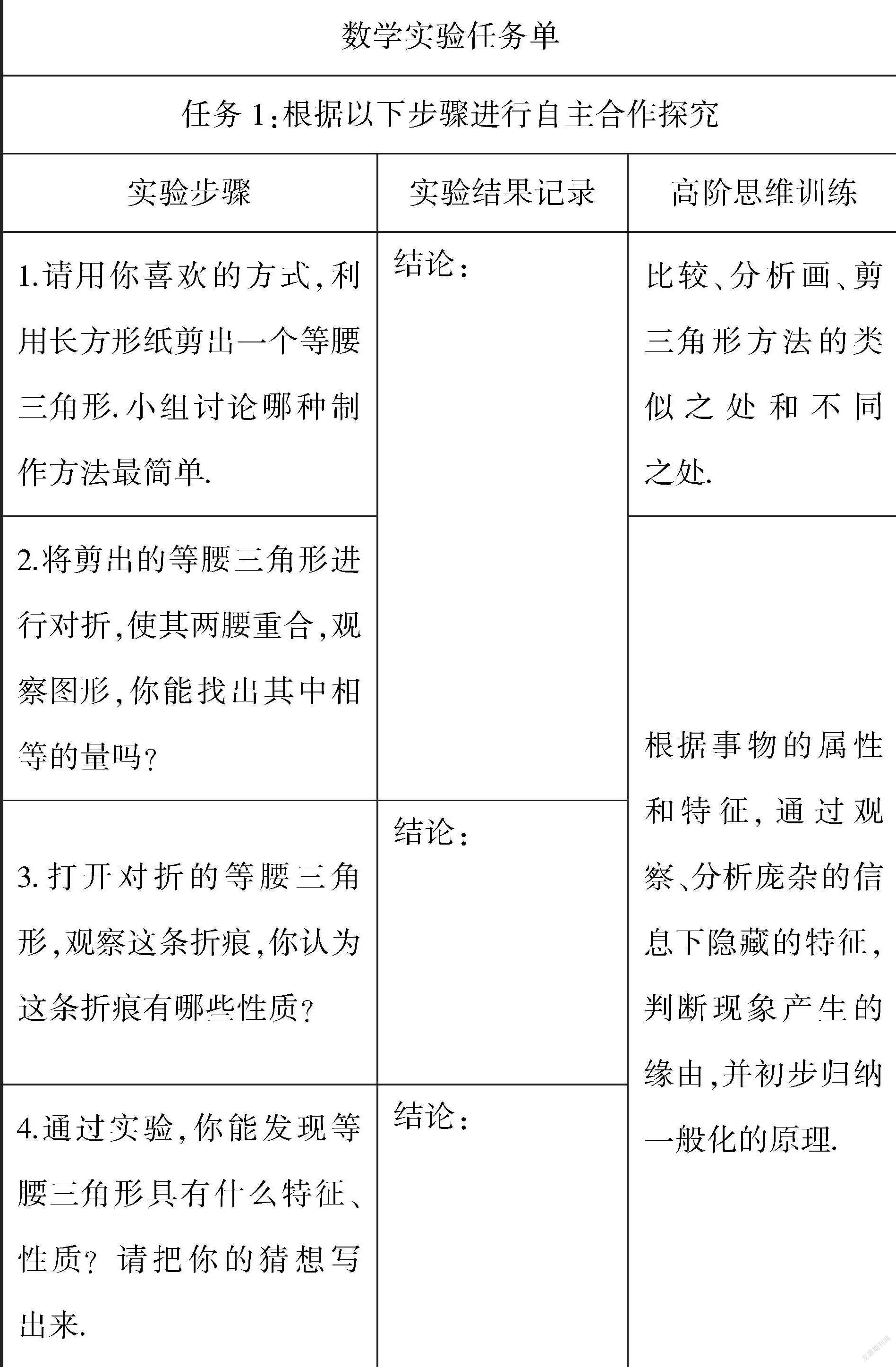
（2）數(shù)學實驗

探究環(huán)節(jié)教師可以以實驗任務單為支架，并結合信息技術幾何畫板的使用，幫助學生開展探究活動.在學生探究的過程中，教師要給予恰當?shù)母深A，如根據(jù)需要及時發(fā)問，提供及時的反饋，提供表達的機會與評價的時間等.

設計意圖：? 讓學生在合作探究的過程中，共享經(jīng)驗，交流爭論，對信息進行分析、篩選，得出等腰三角形兩個性質(zhì)的猜想，發(fā)展學生的批判性思維.

（3）演繹證明

教師在教學的過程中應恰當引導學生發(fā)散思維，用全面的思維考慮問題，發(fā)現(xiàn)問題之間的關聯(lián)，用一題多解證明等腰三角形的性質(zhì)，從而提高學生的綜合能力.本環(huán)節(jié)設計如下兩個核心問題.

設計意圖：? 一題多解，培養(yǎng)學生從不同角度、不同方面去思考問題，提高思維的靈活性和廣闊性.

（4）練習應用

本環(huán)節(jié)的第一道問題回歸生活中的實例——三角形測平架中的奧秘，讓學生認識到數(shù)學來源于生活，又服務于生活.練習題由易到難，利用變式題逐步拔高學生的思維層次.同時，教師要注意學生在做題過程中出現(xiàn)的錯誤，幫助學生從根源剖析錯誤，培養(yǎng)學生思維的嚴謹性.

最后，筆者分享了語文課中的寶塔詩與美術課中的黃金三角形的相關知識，拓展了學生的知識面，讓學生感受跨學科融合的數(shù)學美，深化對等腰三角形性質(zhì)的理解.

（5）小結歸納

本環(huán)節(jié)用問題引導學生對所學的內(nèi)容、思想方法等進行語言表述，升華了數(shù)學的思想方法，同時對學生提出的疑惑加以解釋，幫助學生通過反思達到對知識更深層次的理解，而作業(yè)的分層布置讓不同水平的學生都能在練習和解題中取得收獲.

三、小結

本課從培養(yǎng)學生高階思維能力的教學設計需要關注的六大方面出發(fā)，通過數(shù)學實驗活動、把信息技術作為認知工具、精心設計任務單等，努力為學生營造一個高階學習的氛圍，使學生的思維從低層次的記憶、理解提升到高層次的分析、評價、創(chuàng)造.培養(yǎng)高階思維是時代的要求，但這是需要一個過程的，因此，對于教師而言，我們要設計好以高階學習為支撐的教學設計，有意識地在課堂上利用問題進行高階思維的訓練，讓提高學生的數(shù)學素養(yǎng)成為我們追求的目標.

【參考文獻】

[1]趙生龍，周雪梅.問題式教學下地理高階思維的培養(yǎng)策略[J].中學地理教學參考，2019（12）：22-23.

[2]顧曉東.基于高階思維的數(shù)學學習活動設計策略[J].教學與管理，2019（14）：46-48.

[3]潘星竹，姜強，黃麗，等.“支架+”STEM教學模式設計及實踐研究：面向高階思維能力培養(yǎng)[J].現(xiàn)代遠距離教育，2019（03）：56-64.

[4]李貴安，鄧泓，周詳，等.中學物理教學中高階思維能力的培養(yǎng)探究[J].物理教師，2015，36（08）：2-4，13.

[5]李華.中學英語教學中高階思維能力的培養(yǎng)[J].教育導刊，2013（03）：79-82.

[6]鐘志賢.促進學習者高階思維發(fā)展的教學設計假設[J].電化教育研究，2004（12）：21-28.