考題探究模型解讀，深入賞析教學反思

陳霞

[摘? 要] “一線三等角”模型是重要的幾何模型，該模型中的三個等角頂點位于同一直線上，可形成一組相似關系，中考常以該模型為背景命制探究題. 挖掘模型特點，深入賞析模型有著一定的意義. 文章將探究一道“一線三等角”模型考題，解讀賞析模型，提出相應的教學建議.

[關鍵詞] 幾何;一線三等角;模型;相似三角形;拓展

考題探究

幾何綜合題是中考常考問題類型之一，問題往往以幾何圖形為外在形式構建內在幾何關系，可全面考查學生幾何知識、空間幾何觀以及邏輯思維. 下面以一道幾何探究題為例，進行問題探究.

1. 考題呈現

考題：2020年江蘇宿遷中考數學卷第27題

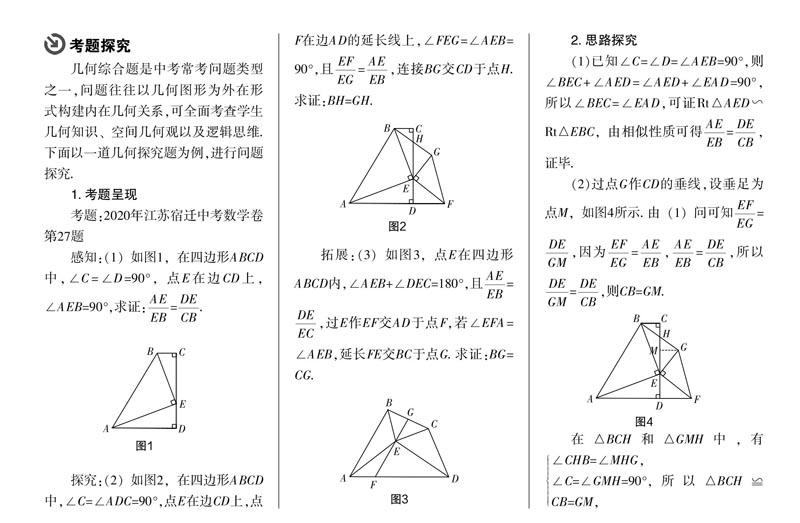
感知：（1）如圖1，在四邊形ABCD中，∠C=∠D=90°，點E在邊CD上，∠AEB=90°，求證：=.

探究：（2）如圖2，在四邊形ABCD中，∠C=∠ADC=90°，點E在邊CD上，點F在邊AD的延長線上，∠FEG=∠AEB=90°，且=，連接BG交CD于點H. 求證：BH=GH.

拓展：（3）如圖3，點E在四邊形ABCD內，∠AEB+∠DEC=180°，且=，過E作EF交AD于點F，若∠EFA=∠AEB，延長FE交BC于點G. 求證：BG=CG.

2. 思路探究

（1）已知∠C=∠D=∠AEB=90°，則∠BEC+∠AED=∠AED+∠EAD=90°，所以∠BEC=∠EAD，可證Rt△AED∽Rt△EBC，由相似性質可得=，證畢.

（2）過點G作CD的垂線，設垂足為點M，如圖4所示. 由（1）問可知=，因為=，=，所以=，則CB=GM.

在△BCH和△GMH中，有∠CHB=∠MHG，∠C=∠GMH=90°，CB=GM，所以△BCH≌△GMH（AAS），則BH=GH.

（3）如圖5所示，在EG上取點M，使得∠BME=∠AFE，過點C作CN∥BM，交EG的延長線于點N，則∠N=∠BMG，推理可得∠EAF=∠BEM，可證△AEF∽△EBM，所以=.

進一步分析可知∠N=∠EFD，∠EDF=∠CEN，可證△DEF∽△ECN，所以=. 又知=，所以=，則BM=CN. 在△BGM和△CGN中，∠BGM=∠CGN，∠BMG=∠N，BM=CN，所以△BGM≌△CGN（AAS），則BG=CG.

3. 問題評析

上述以探究的形式呈現幾何問題，分“感知”“探究”“拓展”三個階段，其中“感知”階段引導學生進行過程探究，總結證明方法，把握圖形特點;“探究”階段則是對模型的進一步深化綜合，引入三角形全等進行論證;而最后的“拓展階段”是對圖形的拓展深化，啟發學生利用上述解題思路構建模型，利用相似轉化、對等轉換、全等轉化來完成思路構建，幾何證明. 實際上，上述考題所基于的是初中幾何“一線三等角”模型，屬于直角型特殊模型，根據該模型可直接構建三角形相似關系，提取線段比例式，深刻理解模型可顯著提升解題效率.

模型解讀

“一線三等角”模型是典型的數學模型，從幾何視角可分為直角型、銳角型和鈍角型，其圖形結構相對簡單. 而從圖形分步視角可將其分為同側型和異側型，如圖6和7.

圖中存在如下關系：在△ABC和△CDE中，點C位于直線BD上，其中∠ACE=∠ABD=∠EDF.

可推得如下結論：相似關系——△ABC∽△CDE;線段比例關系——==;若AC=CE，則可得全等關系△ABC≌△CDE.

上述的同側和異側“一線三等角”模型的結論可由相似轉化得出，該模型的本質特點是有三個等角位于同一條直線上，該等角可以是銳角、鈍角或者直角. 隨著角頂點的位置變化或者角圍繞頂點進行旋轉，會產生相應的衍生圖形，呈現圖形的和諧美，并且模型中的結論依然成立.

深入賞析

“一線三等角”模型具有極高的識別度，在考題中的應用極為廣泛，但同時模型的變形衍生能力較強，綜合性試題中對學生的思維水平有一定的要求，需要結合數學經驗，運用數學方法來加以突破.？搖問題解析過程提取其中的三等角是關鍵，而往往考題以“等角”針對性變式，常將其隱藏，需要進行模型添補，下面結合實例進行探究賞析.

1. 局部隱藏，細節修補

例1：如圖8所示，已知點M是正方形ABCD底邊BC上的一點，且ME⊥AM，ME交AD的延長線于點E. 若AB=12，BM=5，則DE的長為______.

解析? 由于∠B=∠AME=90°， 延長BC，過點E作BC延長線的垂線，設垂足為點N，則可構建“一線三等角”模型，在該模型中∠ABM=∠AME=∠ENM=90°. 由模型結論可得△ABM∽△MNE，則=. 已知AB=EN=12，BM=5，所以DE=CN=MN-（BC-BM）=.

評析? 上述問題中不存在完整的“一線三等角”模型，僅含有一組等角，但通過延長線、作垂直可構建“三等角”. 解題的關鍵是把握其中的等角關系，合理利用圖形特點來作輔助線，將問題條件進行串聯.

2. 一角獨顯，兩側增補

例2：如圖9所示，在四邊形ABCD中，已知AD∥BC，∠BCD=90°，AB=BC+AD，∠DAC=45°，點E位于CD上，且∠BAE=45°. 如果CD=4，則△ABE的面積為______.

解析? 由于∠BAE=45°，過點A作AD的垂線，在該垂線上取點M和N（令點N位于點A下方），使得∠BMA=∠ENA=45°，然后過點E作MN的垂線，設垂足為點F，延長CB交MN于點G，如圖9所示.

分析可知四邊形ADCG為正方形，則AG=CG=CD=4，易知AB=BC+AD，可推知AB=5，BG=3，BC=1. 由于∠BAE=∠M=∠N=45°，由“一線三等角”模型可推知△ABM∽△EAN，由相似性質可得=，代入線段長可解得DE=，則CE=. 由面積割補法可得S=S-S-S=.

評析? 上述問題突破的關鍵是把握其中的“特殊角”，也是構建模型的基礎，解題的思路來源于對“一線三等角”模型的深刻理解、深度思考. 該模型中不僅隱含了基本的幾何知識，還蘊含著相應的思想方法.

3. 線角均藏，構圖全補

例3：如圖10所示為反比例函數y=的圖像，點A（2，3）位于其圖像上，而點B（0，2）位于y軸上. 作射線AB，將射線AB圍繞點A逆時針旋轉45°，與反比例函數圖像的交點設為點C，則點C的坐標為______.

解析? 過點C作AC的垂線，與射線AB的交點設為D，再過點C作x軸的平行線，在平行線上取點E和F，令∠DEC=∠AFC=90°，如圖10所示，則可以構建“一線三等角”模型. 其中∠DAC=45°，由模型結論可得△DEC≌△CFA. 結合點A和點B的坐標可知k=6，直線AB的解析式為y=x+2. 設點C的坐標為a，，可得CF=-a+2，AF=-+3，可推得點D的坐標為a+-3，-a++2，點D位于直線AB上，將其代入解析式可解得a1=-1，a2=2（舍去），所以點C的坐標為（-1，-6）.

評析? 上述考題以圖形旋轉為背景，求解點C坐標很容易聯想到求相關線段長，突破的關鍵是挖掘圖像中的特殊角，適度聯想，探尋圖形之間的聯系，結合解題經驗來構建數學模型. 該問題有著一定的考查深度，對學生的知識經驗和聯想思維有著較高的要求.

教學思考

中考試題中常蘊含一些數學模型，以模型為基礎進行試題衍生，“一線三等角”模型是幾何常見模型之一，模型實質是幾何相似關系，教學中引導學生關注習題，挖掘模型，總結方法規律可顯著提升學生的解題能力，下面提出幾點教學建議.

1. 關注模型特征，培養模型意識

模型來源于對數學規律的總結、知識經驗的積累，是基于知識典型結構的特殊總結，因此模型通常具有鮮明的特征，含有“特殊”性質. 以“一線三等角”模型為例，模型特征為“有三個等角的頂點位于同一直線上”，特性則為“由模型可推得一組相似三角形”. 教學的重點有兩個：一是關注模型特征，二是培養學生的模型意識. 前者需從教材的基本模型入手，指導學生進行特征總結，理解模型結構. 而模型意識的培養則需要引導學生深刻認識模型本質，引導學生進行規律總結，養成模型解題的習慣，提升學生的特殊意識，形成“模式識別”的解題策略.

2. 重視方法講解，拓展數學思維

從上述“一線三等角”模型的探究過程可知，模型并非總是直觀、完整的，有時需要挖掘其中隱藏的特殊角，通過作輔助線的方法來完善. 如上述三道例題在建模過程中經歷了找角、定線、框架三個階段，以特殊角為依托，衍生幾何模型，從而讓圖像直觀化. 在教學中需要重視方法講解，指導學生掌握建模的方法，激發學生的聯想思維，引導學生自主反思、推演、提煉模型，充分掌握幾何模型，做到“舉一反三，解題通法”. 同時在探索模型的過程中，注意總結問題模型，以題為線索，結題成網，形成系統模型，從根本上提升學生的思維能力.

3. 注重知識串聯，滲透建模思想

經典模型往往有著深刻的知識背景，開展模型教學需注重知識串聯，有效探索模型實質，挖掘模型所涉知識，使學生掌握模型的知識鏈. 以上述“一線三等角”模型為例，實則是由等角關系生成的相似關系，由三角形相似生成的線段比例式，其中含有相似三角形的判定、性質等內容，教學中需要引導學生理解模型中的相似內涵. 另外，模型解題過程會涉及定角定線作圖，通過搭框架的方式完善模型，該過程中隱含著數學的建模思想，模型教學中要合理滲透數學思想，讓學生感悟思想內涵，促進學生核心素養的發展.