數學教學的另一種方法

白書寧

【摘要】

幾十年來，數學教育教學在很大程度上依賴于教師向學生展示正確操作的范例練習，作為他們自己練習時的榜樣.近年來，為了給學生進行錯誤分析，引入了不正確的練習.將正確工作的練習與錯誤分析相結合，這給研究人員提出了更高的數學理解.方法：一種混合方法被用來調查在七年級數學單元中對方程和不等式的錯誤分析.定量數據用于建立使用錯誤分析有效性的統計，定性方法用于理解參與者的錯誤分析經驗.結果：測試后得分沒有顯著差異，然而，延遲后測試成績有顯著差異.結論：總的來說，老師和學生發現使用錯誤分析在學習過程中是有益的.

【關鍵詞】錯誤分析;正確和錯誤的例子;數學教學實踐;數學實踐標準

一、引言

幾十年來，數學教育的教學方法基本都是教師在課堂上向學生展示正確的解題步驟，隨后讓學生依據教師演示的步驟進行自我訓練并解答書本或是練習冊上的習題.在數學考試之后也是遵循這樣的流程，教師向學生展示解題的正確步驟，然后讓學生依據正確的答案進行對照和自我修改.這樣的教學方法貌似已經成為數學教學的金科玉律，在以往的教學過程中也沒有遭到什么質疑與抨擊.但隨著社會的快速發展，越來越需要靈活與創新型的人才，而不是一味地遵循硬性規定的員工.數學作為鍛煉邏輯與解決問題能力的基礎學科，教師教授它的目的不是讓學生學會如何考試、如何計算，而是培養學生解決問題的邏輯和思維模式.在這種情況之下，傳統的正確演示式教學就不甚合適，它雖然可以幫助學生取得較好的學業成績，但對于創新性的培養有所欠缺.

由此，錯誤分析法應運而生.錯誤分析法指的是針對學生做錯的題目進行分析，包括犯錯誤的原因以及后果，以往的研究認為分析學生做錯的題目是另一種強化的形式，會導致學生對錯誤的方法更加印象深刻，進而促進個體下次繼續犯同樣的錯誤.但是，最近的研究表明，錯誤分析法并不是強化學生的錯誤做法，而是幫助學生深刻認識到自己出現錯誤的原因，其強化的是學生對自己犯錯誤過程中的錯誤的思維模式，能夠在根本上探析學生的內部認知模式.并且，錯誤分析法可以幫助學生構建全面完整的認知圖式，而不是集中于正確的問題解決方式.錯誤分析法不僅可以從根本上杜絕學生錯誤的思維模式，還能夠完善學生的認知圖式.最終促進學生更好地將該模式遷移到更廣闊的領域之中，更好地迎合社會的需求.然而，目前在數學教學中關于錯誤分析法的研究十分匱乏，因此，本研究擬檢驗錯誤分析法在數學教學中的有效性.

二、研究目的

本研究的目的是探索七年級學生是否可以從正確范例和錯誤分析的使用中將數學學習得更好，而不是從更傳統的解決練習的教學方法中學習，在這種方法中，學生只接受正確范例的指導.這項研究通過調查教師和學生在錯誤分析方面的經驗反饋，進一步推進了以前關于從正確的例子和錯誤分析中學習這一主題.本研究回答了以下問題：

1.當錯誤分析被包括在學生的課程和作業中時，與傳統的僅通過正確例子學習的方法相比，數學成績有什么不同？

2.當錯誤分析包含在學生的課程和作業中時，相對于僅通過正確例子學習的傳統方法，學生和老師觀察到了什么樣的好處或缺點？

三、研究方法

一種混合方法設計被用來調查在七年級數學單元中對方程和不等式的錯誤分析的使用.使用定量數據來建立使用錯誤分析有效性的統計，使用定性方法來理解參與者在錯誤分析方面的經驗.

（一）研究對象

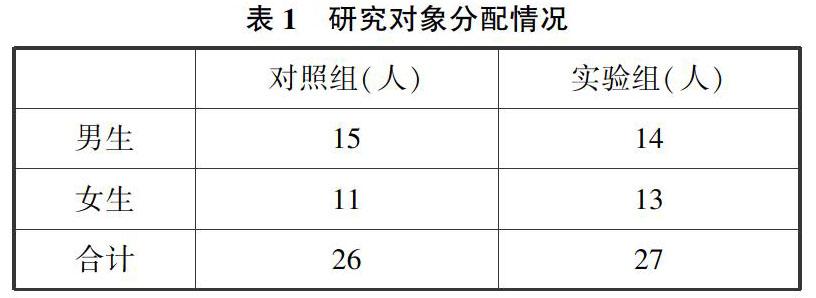
黑龍江省大慶市兩所學校的七年級數學班使用一個方便的分組組成了對照組和實驗組.26名學生為對照組，27名學生為實驗組.同一個老師教兩組學生，所以可以從老師的角度對學生如何學習和參與在兩組間進行比較.在學習開始時，老師愿意在她的教室里嘗試錯誤分析，然而，她并不熱衷于使用這種策略，她無法想象錯誤分析如何在日常工作中發揮作用.到研究結束時，老師變得非常熱衷于在七年級數學課上使用錯誤分析.其中，29名男生，24名女生（如表1）.

（二）研究材料

創建了一個前測和后測，其中包含的問題將使用格倫科數學：你的共同核心版CCSS作為資源來測試對方程和不等式的數學理解.從格倫科數學：你的共同核心版CCSS教科書中為對照組和實驗組都創建了家庭作業，然而，研究人員重寫了兩到三個作業練習作為錯誤的例子，讓實驗組找出錯誤，并用正當理由修正練習.研究人員對兩組學生都使用作業時間日志來跟蹤他們花在家庭作業上的時間.

三、研究結果

進行初步分析以評估t檢驗的假設.這些假設包括：（a）獨立性，（b）用夏皮羅-維爾克檢驗進行正態性檢驗，（c）用萊文統計量進行方差齊性檢驗.所有假設都得到滿足.

前測成績的Levene統計（p>0.05）表明各組間無顯著性差異.進行獨立樣本測試，以確定錯誤分析對學生成績的影響，錯誤分析是由前測和后測以及前測和后測延遲手段的差異決定的.對照組（M=8.23，標準差=5.67）和實驗組（M=9.56，標準差=5.24）的后測得分無顯著差異;t（51）=0.88，p=0.381（如表2）.然而，對照組（M=5.96，標準差=4.90）和實驗組（M=9.41，標準差=4.77）的延遲后測得分有顯著差異;t（51）=2.60，p=0.012（如表3）.這些結果表明，學生可以通過各種方法初步學習數學概念.然而，當錯誤分析被添加到學生的課程、作業和測驗中時，數學知識的保留會顯著增加.值得注意的是，實驗組（M=9.56）與對照組（M=8.23）從前測到后測的平均值之間的差異更大，這意味著即使平均值沒有顯著差異，實驗組確實顯示出更大改善.

由于通過讓每組中的一小部分人參與跟蹤完成家庭作業所花費的時間，因此測試分析的結果不能用于任何概括.然而，分析的結果很有趣.使用獨立的樣本t檢驗來計算和分析每組完成作業所花費的平均時間.對照組（男性=168.30，標準差=77.41）和實驗組（男性=165.80，標準差=26.53）學生花在家庭作業上的時間沒有顯著差異;t（13）=0.07，p=0.946（如表4）.這些結果表明，學生花在家庭作業上的時間幾乎是一樣的，不管他們是必須進行錯誤分析（找出錯誤，糾正錯誤，并證明所采取的步驟是正確的），還是以傳統的方式按照正確的例子解決每個練習.盡管學生課外做作業的時間沒有明顯不同，但實驗組在課堂上確實花了更多的時間進行測驗修正和討論錯誤，這些錯誤可以歸因于知識的保留.

四、討論

研究結果表明，教師采用正確演示法與錯誤分析法對學生進行教學的即時效果沒有顯著差異，這說明學生在接觸數學的新知識的時候，教師采用正確演示法與錯誤分析法都可以很好地被學生接受，這可能是因為學生在構建新的知識圖式時只是在進行知識納入而不進行更為深層次的加工，不管是什么樣的知識輸入方式，都會經過相同的知識輸入路徑，因此，在教授新的數學概念和知識時，教師可以依據自己的教學習慣任意選擇傳統的正確演示法或錯誤分析法.進一步的研究結果還表明，在舊知識的鞏固上，錯誤分析法比正確教學法的效果更佳.這說明錯誤分析法能夠將舊知識進行更好的提取，并且進行更深層次的記憶.這提示教師在復習舊知識的時候應該盡量采用錯誤分析法.

五、結論

通過實證研究本研究得出以下結論：

（1）教授新知識的過程中，數學教師采用正確演示法與錯誤分析法的教學效果沒有顯著差異.

（2）鞏固舊知識的過程中，數學教師采用錯誤分析法的教學效果更佳.

（3）錯誤分析法對教師的教和學生的學都很有益處.

【參考文獻】

[1]Using erroneous examples to improve mathematics learning with a web-based tutoring system[J].Computers in Human Behavior， 2014， 36：401-411.

[2]Glencoe M G， McGrawHill/Glencoe.Algebra 2 Student Edition CCSS[J].Business & Economics， 2012.

[3]Mclaren B M， Adams D M， Mayer R E.Delayed Learning Effects with Erroneous Examples： a Study of Learning Decimals with a Web-Based Tutor[J].International Journal of Artificial Intelligence in Education， 2015， 25（4）：520-542.

[4]Tan Sisman G， Aksu M.A Study on Sixth Grade Students Misconceptions and Errors in Spatial Measurement： Length， Area， and Volume[J].International Journal of Science and Mathematics Education， 2016， 14（7）：1293-1319.

[5]Tsovaltzi D， Melis E， Mclaren B M， et al.Learning from erroneous examples： when and how do students benefit from them[M].Sustaining TEL： From Innovation to Learning and Practice，2010.

[6]Corder， S.P.The Significance of Learners Errors.[J].International Review of Applied Linguistics， 1967， （4）： 161 - 170.

[7]Jiabin Liu，Qinghe Fang，Anxin Guo，Hui Li.Error analysis of reconstructed wave force on a circular cylinder by using wave elevation data[J].Ocean Engineering，2020，209.

[8]陳俊杰.小學生分數除法錯誤研究[D].濟南：山東師范大學，2018.

[9]藺云.高等數學習題錯誤分析及教學對策[J].高師理科學刊，2015（07）：73-78.

[10]杜廣華.對比分析法、錯誤分析法和語際語理論間的關系（英文）[J].山西農業大學學報，1997（04）：77-79+95.

[11]李善良.數學概念學習中的錯誤分析[J].數學教育學報， 2002（03）：6-11.

[12]王槐晟，蘭德新，詹佩玲.談數學教學中的錯誤分析、預防與利用[J].數學之友，2019（08）：6-10.

[13]高宇.初中生數學解題錯誤糾正策略效果研究[D].長沙：湖南師范大學，2017.

[14]李琛.初中生數學運算錯誤診斷分析：以蘇科版教材七年級下教學內容為例[J].中學數學月刊，2016（12）：36-38.

[15]王鵬飛.數學教學中學生“錯誤觀”的調查與分析[J].西部素質教育，2016（03）：7-9.

[16]楊麗蓉.初中生有理數學習中的錯誤分析及教學對策研究[D].上海：上海師范大學，2015.