基于多元教學手段下線性代數立體化教學模式研究

李敏 陳佑軍

【摘要】通過對線性代數教學改革成果的研究，我們發現線性代數立體化教學模式是以簡捷、應用性強、容易理解為目標，應用于教學內容、教學方法、教學手段等方面的教學模式.該模式能夠讓學生全面掌握所學知識，學會使用數學軟件，受到學生歡迎.通過思維導圖，學生可以多角度、立體化地理解所學的知識點，從而把零碎的概念及知識點整合起來，這樣學習起來更方便，不但減少了煩瑣過程，而且能夠增強學生學習數學的興趣，提高其解決實際問題的能力.線性代數立體化教學研究，彌補了單一教學方式的局限性、片面性，為線性代數教學改革提供了新的方向.

【關鍵詞】

教學法;矩陣;MATLAB;思維導圖

線性代數在教學改革中取得了一系列成就，如分層教學法、對分課堂、翻轉課堂等教學法在課堂教學實踐中取得了令人矚目的成績.教師利用信息技術，將慕課、微課等教學方式融入線性代數的日常學習，極大地拓寬了同學們的學習視野，激發了學生的學習興趣，提高了線性代數教學的實效性.

教學有法，教無定法.單一的教學方式有其局限性.在多種教學手段下，線性代數立體化教學彌補了這種片面性，使教學效果更圓滿，提高了學生主動學習的積極性.

1 線性代數立體化教學模式

依據線性代數的教學大綱，根據教學內容的不同，利用信息技術，采用不同的教學方法、教學手段，使學生掌握數學基本內容、基本技能，達到教學要求，完成教學任務的方法稱為線性代數立體化法.其特點是：

1.目標明確，以簡捷、易接受的教學手段、方法，使學生掌握知識.

2.因材施教，方法靈活，不拘一格.

3.充分調動學生學習的主動性，激發學生的學習興趣.

4.通過學習，使學生掌握MATLAB等數學軟件，提高學生掌握信息技術的能力.

5.注重理論與實際相結合，提高學生運用所學知識解決實際問題的能力.線性代數立體化法的必要條件是教師精通多種教學方法，掌握先進的教學手段，熟悉教學內容;教師熱愛教學研究，教學經驗豐富.

2 線性代數立體化教學模式應用

2.1 教學內容、教學方法上的立體化教學應用

線性代數矩陣的乘法是很重要也是非常獨特的運算方法.教師若正常講授，學生也很容易掌握，但教師如果采用啟發式教學，引導學生主動思考，會得到很多意想不到的結論.教材中介紹矩陣的乘法的定義是Am×s×Bs×n=Cm×n，即第一個矩陣的列數與第二個矩陣的行數相同時，矩陣乘法成立，新矩陣的行數、列數分別等于第一個矩陣行數、第二個矩陣的列數.

教師啟發學生思考如下問題：①As×m×Bn×s=？，如果能運算，怎樣定義乘法運算，有什么規律？

②一個下標交叉位置數字不變，即Am×s×Bn×s=？成立，或者As×m×Bs×n=？成立，怎樣定義乘法運算，有什么結果，這兩個結果之間有什么關系？同學們被這些問題吸引了，找出不同類型的實際例子，闡述自己的想法.

教師在這一基礎上，進一步提出矩陣相乘.這種運算規律在其他領域中應用，結果如何，值得同學們進一步思考.

2.2 知識點橫向、縱向相關聯思維導圖

學生由于受各種原因影響，對所學知識掌握得比較片面、零碎，根據這一特點，教師在教學中應注意把知識點橫向、縱向及時貫通，利用思維導圖，把知識點聯系在一起，幫助學生建立系統的、完整的線性代數理論體系.教師通過建立完整的理論體系，幫助學生完成對各個知識點的理解，解決其學習中遇到的各種困惑，協助學生排憂解難，達到融會貫通的目標.

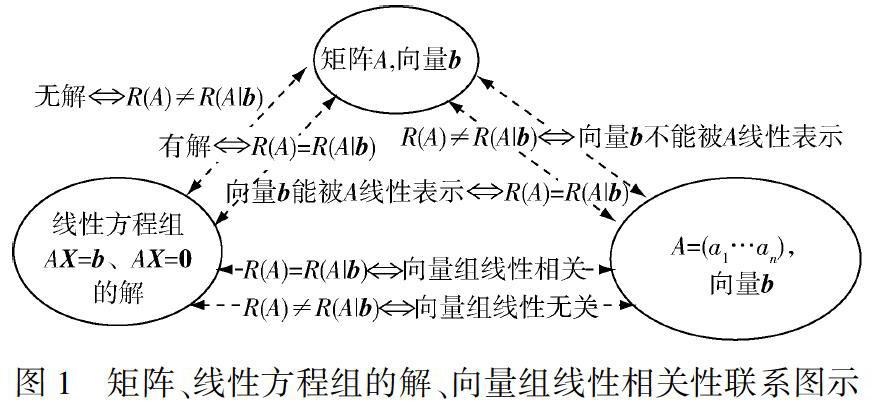
由于學生對線性方程組的解、矩陣的秩、向量組的線性相關性這些概念理解得不全面，因此教師應建立橫向思維導圖，學生根據圖示描述就很快能掌握它們之間的關系，并能根據它們之間的關系解決相應的問題，如圖1.

矩陣是貫串于線性代數各章節的概念，在不同的章節，定義了相應的矩陣.因此學生在學習過程中，感覺概念多，知識點分散，掌握難度比較大.教師在教學過程中，應在詳細剖析各類矩陣的概念之后，把各類矩陣縱向聯系起來，這樣可以幫助學生把各類零碎的矩陣概念統一起來，建立完整的矩陣體系，如圖2.

2.3 教學手段上立體化教學應用

實對稱矩陣可以對角化這個原理，由于解題量大，步驟比較多，學生容易對其產生厭煩心理.在學生掌握概念及解題思想的基礎上，教師可以教學生使用數學軟件MATLAB，

幫助學生樹立使用數學技術及現代工具思想，讓計算機技術真正走進我們的教學.學生在學習軟件的同時，感受新技術的便捷，領略數學的魅力，這樣有利于增強其學習興趣.

在教學中，教師要求學生用正交矩陣將實對稱矩陣對角化.例如，對對稱矩陣 進行對角化.在學生全面掌握計算方法，正確求解后，教師可以要求學生在數學軟件MATLAB中演示用正交矩陣將實對稱矩陣對角化的算法.學生通過以下操作，對實對稱矩陣A進行對角化.

解：在MATLAB命令窗口中輸入命令

計算結果中，矩陣P的列向量就是正交化向量組，D就是對角化的結果.

學生通過操作，深感計算機強大的計算能力，也為自己掌握一門軟件技術感到自豪，增強了學好線性代數的自信心.

3 線性代數立體化教學模式應用效果

通過多年的教學研究，線性代數立體化教學模式應用效果比較明顯，表現在如下方面：卷一的通過率由原來的65[WTB3]%[WTBX]提升到78[WTB3]%[WTBX];卷二的通過率由最初的62.5[WTB3]%[WTBX]逐年遞增4[WTB3]%[WTBX]，個別好的班級，超過85[WTB3]%[WTBX];課程組平均通過率保持在75[WTB3]%[WTBX]左右;學生在考研中，線性代數的得分率逐年提高.部分學生受到學習線性代數的影響，學習數學的興趣與熱情得到提升，學習成績提高，自信心增加，在老師的鼓勵下，參加MATLAB選修課、數學協會的人數增多，參加數學競賽的積極性提高.2018年全國數學競賽，我校學生獲得國家級一等獎1名、二等獎3名、三等獎11名，獲獎率6.8[WTB3]%[WTBX]，獲山東省一等獎6名、二等獎9名、三等獎37名，獲獎率23.6[WTB3]%[WTBX].線性代數立體化教學模式，使學生全面掌握了數學基本內容、基本方法，學會使用數學軟件，增強了解決實際問題的能力.學生通過思維導圖，多角度、立體化理解所學的知識點，把零碎的概念及知識點聯系起來.這樣學生學習起來既方便又效果好，減少了煩瑣過程.這種方式受到了學生的歡迎，增強了學生學習數學的興趣.

4 結束語

通過對線性代數立體化教學模式的研究，我們取得了一定的成績，教師的教學方法、教學手段不斷提高、完善，學生的學習興趣得到增強，主動學習的人數不斷增多.我們也發現了一些需要進一步提高的方面，如教師在課堂教學方面需不斷調整，教學手段需進一步更新，要以簡捷、高效、易理解的方式，使學生領會所講知識.線性代數的數學實驗課急需進一步完善，要和教材相結合，形成系統的、操作性強的、配套的統一體.

【參考文獻】

[1] 杜燕飛，肖鵬.基于MOOC的線性代數混合式教學模式的研究[J].內江科技，2019 （05）：150-151.

[2] [JP3]房秀芬，黃廷祝，蒲和平.線性代數課程小班化：探究式教學模式的實踐與思考[J].大學數學，2018 （06）：41-44.

[3] 高婧.高校線性代數“翻轉課堂”教學模式的研究[J]. 武漢工業學院學報，2018 （04）：112-116.

[4] 張艷艷.線性代數雙型新教學模式的探索與實踐[J].教育現代化，2018 （04）：94-95.

[5] [JP3]薛冬梅，李智.基于移動終端的《線性代數》課程教學模式的研究與實踐[J].吉林化工學院學報，2018 （10）：66-69.

[6] 程麗.基于CDIO教育理念的線性代數教學模式研究[J].赤峰學院學報（自然科學版），2017（18）：9-10.

[7] 李敏，陳佑軍.基于高等數學教學實效性研究調查分析報告[J].教育教學論壇，2019（12）：120-121.

[8] 邰志艷.“互聯網+”背景下線性代數課程教學模式改革的研究[J].中國校外教育，2016（04）：27-30.

[9] 陶霞，張映輝.《線性代數》課程新型教學模式探討[J].湖南理工學院學報（自然科學版），2015（02）：90-94.

[10] 杜美華.基于培養卓越應用型人才的線性代數問題驅動與案例任務教學模式改革[J].青海師范大學學報（自然科學版），2015（02）：27-30.