初中數學幾何變換思想的教學策略研究

林彩琴

【摘要】數學是一門邏輯性強、抽象性強的綜合性學科，注重對學生數學邏輯以及抽象能力的培養.在進行數學教學時，培養學生的數學邏輯、抽象能力以及空間結構想象力非常重要.這一點體現在初中數學幾何的教學上，教師是從根本上觸發學生的數學思維，激發學生的想象力，培養學生的數學素養.因此，培養學生的數學幾何變換思想是初中數學教學工作的重點.但是在實際教學中，教師對數學幾何變換思想的變換還存在許多的問題，培養學生的數學幾何變換思想效果不佳.本文就初中數學幾何變換思想的教學進行討論和研究，希望能為初中數學幾何教學的進步提供一些幫助，更好地促進學生的數學發展.

【關鍵詞】初中數學、幾何變換思想、數學素養、教學

一、建構初中數學中的幾何教學

（一）初中數學中幾何變換思想的概念

初中數學的幾何教學是讓學生學習三角形、正方形、長方形、多邊形等圖形的性質、形狀、功能，研究它們的空間結構以及實際應用.在此過程中，重視學生的主體探究過程以及學生的建模、變換、轉化等思維方法的發展，這對學生的數學思維有重要的作用.

（二）初中數學幾何教學的現狀

在教學初中數學幾何時，部分教師認為只要能懂得一些基本的幾何知識，知道一些基本的圖形性質和特點就可以了.因此，教師只在教學中強調學生對圖形的理解和記憶，沒有注重學生對圖形的思考及轉換，這直接導致了學生的抽象思維能力沒有得到應有的鍛煉，學生不能從多個方面去思考和發現數學問題，這不利于學生對數學的理解和學習，進而影響了整個數學教學工作的進展，學生的能力得不到加強.同時，這不符合當下新課程標準的改革，不利于學生的全面發展.

（三）變換思想對學生學習幾何的重要性

初中數學幾何的教學主要是讓學生對基本圖形有簡單的認知和了解，知道圖形的性質和結構，為以后高中甚至大學的學習打下基礎。同時，數學更是一門具有綜合性、抽象性的學科，當教師教學初中數學幾何時，學生的思維得到了訓練，學生的數學抽象能力得到了提高，學生的發散性思維得到了鍛煉.

例1問題1，如圖1、圖2，鈍角三角形ABC的面積為20，最長邊AB=10，BD平分∠ABC，M、N分別是BD，BC上的動點，求CM+MN的最小值.

分析作點C關于BD的對稱點點E，過點E作EN⊥CB于點N，EN就是CM+MN的最小值.

問題2，如圖3、圖4，三角形ABC為等腰直角三角形，AC=BC=4，∠BCD=15°，點P是CD上的動點，求│PA-PB│的最大值.

分析作點A關于CD的對稱點點E，連接CE，EB，并延長EB交CD延長線于點P，EB的長就是

│PA-PB│的最大值.

這兩個例題之間可形成“手拉手”的變換方式.

因此，教師將變換思想融入學生的數學教學中能極大地激發學生學習數學的興趣，提高數學課堂教學質量和學習效率，讓學生從本質上學好數學，更加深入地了解和理解數學，讓學生能夠在數學學習中進行思考，甚至是創新，進而提高學生的自主學習能力，讓學生能夠從多個角度去思考問題，對學生未來的發展是有極大好處的.

二、在初中數學教學中培養學生幾何變換思想的方法和策略

（一）培養學生幾何的解題興趣

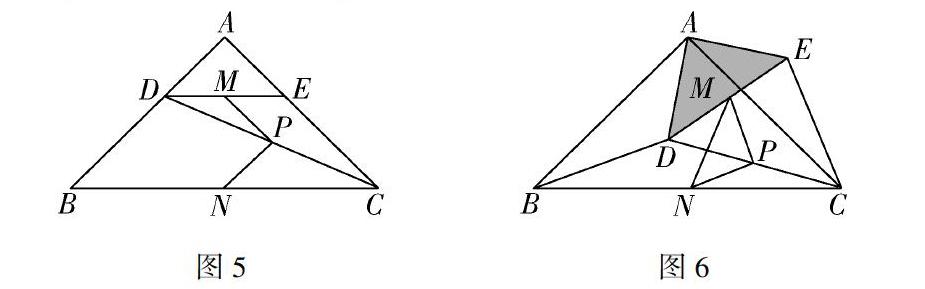
初中數學的幾何學習是最基礎的幾何學習，是對平面圖形的結構和特點的認知，但這樣的學習仍離不開興趣.如果學生對幾何學習有著極大的興趣，就能夠主動學習幾何知識，進而研究它的知識結構和特點.例如，如圖5，在Rt△ABC中，∠A=90°，AB=AC，點D，E分別在邊AB，AC上，AD=AE，連接DC，點M，P，N分別為DE，DC，BC的中點.

1.觀察猜想：

圖5中，線段PM與PN的數量關系是，位置關系是.

2.探究證明：

把△ADE繞點A逆時針方向旋轉到圖6的位置，連接MN，BD，CE，判斷△PMN的形狀，并說明理由.

3.拓展延伸：

把△ADE繞點A在平面內自由旋轉，若AD=4、AB=10，則請直接寫出△PMN面積的最大值.

教師在解題過程中主要給予學生適當的點撥與啟發，關注學生的思考方向，使學生能夠利用圖形進行合適的變換，激發學生探究幾何學習的積極性.因此，在進行幾何教學時，教師應該先培養學生的學習興趣，讓學生對幾何產生興趣，這樣才能激發學生學習幾何的積極性，才能讓學生在學習幾何的過程中主動參與、積極思考.只有這樣，才有利于培養學生的幾何變換思想，才能更好地促進教師教學幾何.

（二）教會學生正確的解題方法

簡單來說，幾何數字就是圖形的教學.因此，如果要培養學生的幾何變換思想，就要讓學生對圖形有一定的認知和印象。例如，三角形是什么樣的？正方形是什么樣的？三角形的勾股定理在正方形的哪種情況下能夠運用？這些知識的轉換需要讓學生清楚正方形的特性、三角形的特性、正方形和三角形的關系，即兩個三角形可以組成一個正方形，但這樣的三角形又得具備什么樣的條件呢？

例2已知，如圖7①，△ABC中，AB=BC，∠ABC=90°，D為AB的中點，過點B作直線BE與CD垂直，交AC于點E.求證：∠ADE=∠CDB.

分析因為△ABC是等腰直角三角形，所以可將它補成一個正方形ABCF，欲證∠ADE=∠CDB，由于兩角沒有直接聯系，考慮證這兩個角都等于某個角，從而使問題得到解決.

證明如圖7②，分別過點A、C作AB、BC的垂線，兩線相交于點F，延長BE交AF于點G，四邊形ABCF是正方形.

∵∠1+∠3=90°，∠2+∠3=90°，∴∠1=∠2.在△ABG和△BCD中，∠1=∠2，AB=BC，∠BAG=∠CBD，∴△ABG≌△BCD∴∠4=∠CDB，AG=BD=AD.在△AGE和△ADE中，AG=AD，∠6=∠5，AE=AE.

∴△AGE≌△ADE.∴∠4=∠ADE，∴∠ADE=∠CDB.

點評對于等腰直角三角形及含有45°角的三角形來說，根據解題的需要，經常可以將原圖形補成正方形，以充分運用正方形、直角三角形的性質來解題.

例3定義：按螺旋式分別延長n邊形的n條邊至一點，若順次連接這些點所得的圖形與原多邊形相似，則稱它為原圖形的螺旋相似圖形.

如圖8，分別延長多邊形A1，A2，…，An的邊得A1′，A2′，…，An′，若多邊形A1′A2′，…，An′與多邊形A1，A2，…，An相似，則多邊形A1′，A2′，…，An′就是A1，A2，…，An的螺旋相似圖形.

如圖9，已知△ABC是等邊三角形，作出△ABC的一個螺旋相似圖形，簡述作法，并給出證明.

如圖10，已知矩形ABCD，請探索矩形ABCD是否存在螺旋相似圖形，若存在，則求出此時AB與BC的比值;若不存在，則請說明理由.

如圖11，△ABC是等腰直角三角形，AC=BC=2，分別延長CA，AB，BC至A′，B′，C′，使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC，請直接寫出BB′，CC′的長（用含k的代數式表示）.

分析如圖9，延長AB到點E，延長BC到點F，延長CA到點D，使得BE=CF=AD，連接EF，DF，DE，△DEF是△ABC的一個螺旋相似圖形，證明△DEF是等邊三角形即可解決問題.

如圖10，假設存在，矩形EFGH是矩形ABCD的螺旋相似圖形，設AB=CD=a，BC=AD=b，BE=DG=x，CF=AH=y.分兩種情形，利用相似三角形的性質以及相似矩形的性質，構建關系式證明a=b即可解決問題.

如圖11，作B′T⊥CB交CB的延長線于點T.設TB=TB′=m，證明△A′CC′≌△A′TB′（ASA），推出A′C=TC′，CC′=TB′=BT，構建關系式證明m=k即可解決問題.

像此類新定義題型，學生只有把握基本的圖形概念，了解圖形，才能讓圖形進行轉換。同時，只有進行類比運用，才能培養學生的幾何變換思想，才能進一步加深學生對幾何圖形的理解和記憶.

（三）結合模具進行有效教學

幾何知識的學習具有很強的空閑性，需要學生具有一定的抽象思維，而多數初中生沒有抽象思維的概念，抽象能力比較弱.

教師應該在教學中考慮學生的實際情況，結合模具進行教學，如在研究兩點距離最短時，教師可以將數學理論知識和模具相結合，先講一部分理論知識，再在模具上進行實驗，甚至可以讓學生自己進行實際驗證，這樣一來，課堂不再是教師的獨角戲，而是讓學生參與課堂，充分調動了學生學習的積極性和主動性.

（四）聯系實際，運用日常生活策略

數學本來就是從生活中來，回到生活中去.因此，在教學中，教師應該先結合實際生活情況，讓學生思考生活中的幾何問題，想辦法解決問題，再進行指導教學.例如，如圖12，正方形ABCD是旅游區域示意圖，△ABC部分表示湖面水域.游客在湖岸AB等候乘船，游船從點B出發送游客去湖對岸AC，下船游玩后返回湖對岸AB的上岸點M處，M為AB的中點，游船怎樣航行路程最短？如果湖岸AB長為500米，那么游船行駛的最短距離是多少米？

分析作點B關于AC的對稱點點D，連接DM.本題是生活中游船的最短航行路徑問題，可變換為數學中通過軸對稱求線段和的最小值問題.

這樣一來，架設起生活與數學的橋梁，把數學知識生活化，讓學生體會到生活中時刻存在數學知識，既鍛煉了學生的幾何變換思維，又鍛煉了學生在實際生活中運用數學的能力，這對學生未來的發展和生活有極大的好處.

三、夯實基礎，提升素養

初中數學幾何是為了給以后更高層次的幾何學習打下基礎.初中數學幾何的教學不是一朝一夕就能完成的，只要我們勤揣摩，就能有效地培養學生的幾何變換思想，讓學生經歷陳述性知識→程序性知識→自動化知識的過程，從本質上理解數學的抽象思維，讓學生得到更好的鍛煉和發展，提升學生的數學核心素養.

【參考文獻】

【1】甘生達.初中數學幾何變換思想的教學策略研究[J].新課程（中），2018（8）：26.

【2】劉明.給力的旋轉，改變圖形位置關系的利器[J].數學教學通訊，2017（11）：77-78.

【3】潘玉.初中數學幾何變換思想的教學策略[J].中學生數理化（教與學），2015（8）：96.