棉紗毛羽根數和毛羽H 值的相關性研究
莊粟裕 韓家寶 馬宏慶 徐 陽
[1.江南大學,江蘇無錫,214122;2.烏斯特技術(蘇州)有限公司,江蘇蘇州,215122]
毛羽是指纖維頭尾端或中間段暴露在紗線主體以外的部分,有端毛羽、圈毛羽和浮游毛羽3種基本形態[1]。毛羽過多不僅會影響紗線表面的光潔程度和光澤,還會影響織造工序的生產效率以及成品的性能和外觀質量[2],因此,紗線毛羽是反映紗線質量的重要指標之一[3]。傳統的毛羽評價主要包含毛羽根數(S1+2,S3)、毛羽H 值等指標。毛羽根數S1+2,指100 m 紗線上單側面1 mm和2 mm 長度級別內的毛羽數量,S3則指100 m 紗線上單側面3 mm 及3 mm 以上的毛羽根數總和;而毛羽H 值是指1 cm 單位長度紗線中毛羽長度之和與1 cm 的比值,無量綱[4]。毛羽根數可對毛羽進行分級,并能反映長短毛羽對紗線的危害程度,主要用于指導紡紗生產過程質量控制,但存在可重現性較差、準確性較差等缺點;而毛羽H值能表示單位長度上總體毛羽量,且測試結果穩定,常用于紗線貿易及質量說明,但不能反映長短毛羽的數量,因此兩個指標經常綜合使用來進行毛羽評價[5]。
在實際生產中,常見的毛羽測試儀器有烏斯特UT5 型條干儀,HL400 型毛羽儀、YG172B 型毛羽儀等。傳統儀器在測試毛羽根數時,易因毛羽自然卷曲、毛羽各方向分布不勻以及空氣阻力等因素使毛羽形態發生改變,導致測試結果不能如實反映真實毛羽長度,準確度和可重復性較差。針對這一點,烏斯特研發了UT6 型條干儀,并提出了真實毛羽根數S1+2u和S3u等新的輸出指標。
本研究對毛羽根數和毛羽H 值之間的關系進行探討,重點探究兩者間的相關性,建立回歸模型,為企業更合理地評價毛羽提供理論基礎。
1 試驗
1.1 測試試樣
本研究的試驗原料為由各個廠家送到烏斯特實驗室測試的樣品,批次各不相同,所以得到的試驗數據具有普遍代表性,樣本具體見表1。
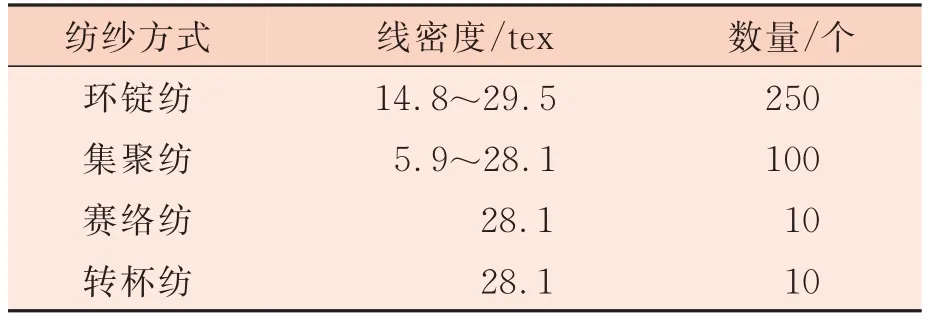
表1 不同紡紗方式的棉紗樣本信息
1.2 測試方法
1.2.1 測試原理
UT6 HL 模塊的測試原理是基于FZ/T 01086—2000《紡織品 紗線毛羽測定方法 投影計數法》改進的新投影計數法。工作原理:在紗線經過測試區域時,將壓縮空氣吹入到測試區域,使紗體上的突出纖維達到其真正長度以確定實際的毛羽分級。
UT6 OH 模塊測試毛羽采用的是漫反射法。工作原理:一束持續的單色平行光源照射在紗線上,紗體暗,而紗體上的毛羽亮,散射光被透鏡系統集聚并被光學傳感器檢測到,輸出為電信號[6],進而被UT6 的計算機評估為毛羽H 值。
1.2.2 試驗條件
由經過標準培訓的烏斯特實驗室工程師進行試驗,采用同一試驗員和統一標準操作手法。
試驗條件滿足GB/T 6529—2008《紡織品調濕和試驗用標準大氣》:相對濕度(65±4)%,溫度(20±2)℃,且儀器和樣品處于同一室,同一溫濕度環境中。UT6 型條干儀每周進行校準檢查,數據合格后才能進行其他試驗的測試。
1.2.3 試驗儀器及相關參數
采集不同紡紗形式生產的棉紗(具體參數見表1),運用UT6 型條干儀的毛羽測試模塊(HL模塊和OH 模塊)對各管紗進行測試,測試速度400 m/min,測試時間2.5 min,測試長度1 000 m。HL 模塊輸出的毛羽根數指標:1 mm、2 mm、3 mm、4 mm、6 mm、8 mm、10 mm、S1+2u和S3u根數;OH 模塊輸出毛羽H 值。為了方便計算,將S1+2u和S3u除以1 000,獲得對應的S1+2u/1 000 和S3u/1 000。
2 測試結果與分析
2.1 一元回歸分析
運用統計分析軟件SPSS 中給出的10 種曲線模型對不同紡紗方式生產的棉紗毛羽數據進行一元回歸分析,經過決定系數比較以及預測模型顯著性判斷,選擇出其中預測效果最優的模型,結果見表2 和表3。

表2 S1+2u/1 000 與毛羽H 值一元回歸分析結果

表3 S3u/1 000 與毛羽H 值的一元回歸分析結果
設具有相關關系的兩個變量分別為x、y,其中y 為因變量,代表UT6 OH 模塊輸出結果毛羽H值,x1為UT6 HL 模 塊 輸 出 結 果S1+2u,x2為UT6 HL 模塊輸出結果S3u。
由表2 和表3 可知,對純棉紗整體數據進行一元回歸模型擬合的結果中,S1+2u的預測效果優于S3u,可能是由于純棉紗中短毛羽量占比較多,有研究表明占65%以上[7],更貼近測量整體毛羽的毛羽值。對于S1+2u預測模型的決定系數,環錠紡>賽絡紡>集聚紡>全部數據>轉杯紡,其中前三者的決定系數均大于0.800,說明UT6兩模塊的預測穩定性很好,全部數據和轉杯紡的預測結果也較好;對于S3u預測模型的相關系數,環錠紡>全部數據>集聚紡>賽絡紡,轉杯紡無最優預測模型。
表4 是不同紡紗方式的純棉28.1 tex 紗的毛羽與對應的環錠紗的比較結果。毛羽H′值指不同紡紗形式毛羽H 值/環錠紡毛羽H 值;S1+2u′指不同紡紗形式S1+2u/環錠紡S1+2u;S3u′指不同紡紗形式S3u/環錠紡S3u。

表4 純棉28.1 tex 樣本的毛羽數據平均值及比較值
2.2 多元回歸分析
由于賽絡紡、轉杯紡樣本的一元回歸分析效果相對較差,考慮到多元線性回歸可選擇多個自變量進行分析,于是選用多元線性回歸模型進一步建立預測模型,以獲得影響毛羽H 值的最優預測方程。研究顯示,逐步回歸分析能夠建立最優線性回歸模型,其結果不僅優于進入和向后,而且簡單易行,預測精度較高,因此本研究選用逐步回歸分析的方法[8]。先計算各影響變量與毛羽H 值的相關性,然后確認對因變量具有較強影響的變量作為輸入變量。
表5 所示為1 mm、2 mm、3 mm、4 mm、6 mm、S3u/1 000(1.038S3u/1000)與毛羽H 值的雙變量皮爾遜相關性分析。根據分析結果篩選多元回歸分析的輸入變量為:1 mm、2 mm、3 mm 毛羽根數 和 逆S1+2u/1 000、冪S3u/1 000。表5 中,**表示α<0.01 水平顯著;*表示α<0.05 水平顯著,下同。賽絡紡樣本多元回歸分析結果見表6 和表7。表6 中,a 表示預測變量,常量,逆S1+2u/1 000;b表示預測變量,常量,逆S1+2u/1 000,冪S3u/1 000;c 表示因變量,毛羽H 值。
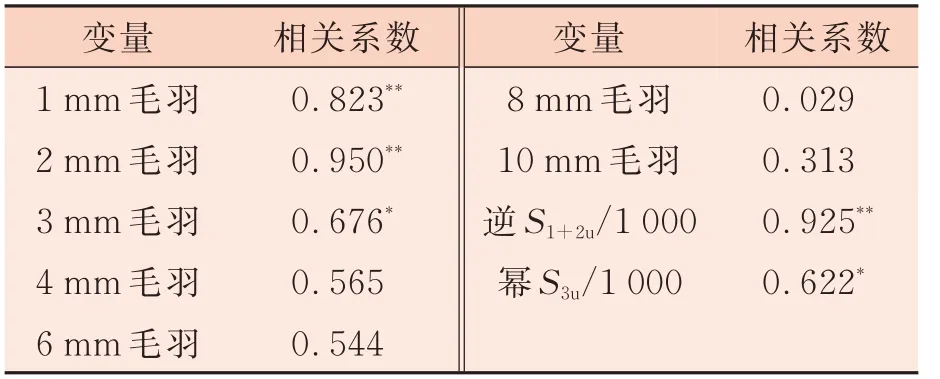
表5 賽絡紡雙變量相關性分析
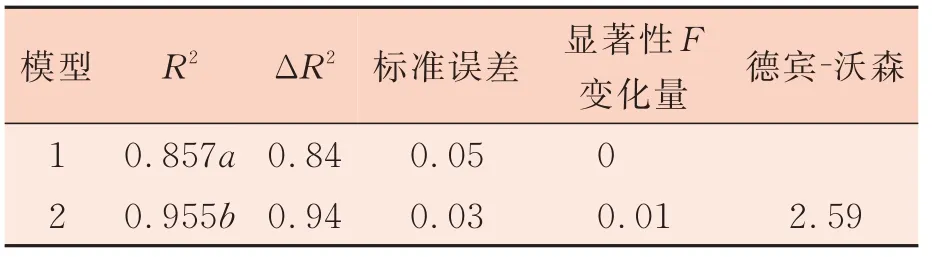
表6 賽絡紡樣本多元回歸分析參數匯總
根據逐步回歸分析回歸系數結果,獲得兩個模型,兩者顯著性均在α<0.05 水平顯著。且模型2 的自變量的容差為0.87,VIF 為1.14,接近于1,說明這些自變量之間共線性弱;殘差項差異德賓?沃森值為2.59,接近2,說明殘差項之間不相關;且模型2 的決定系數高于模型1,為0.955,體現了很高的回歸模型的解釋百分比。因此獲得最優 預 測 模 型 為2.486×1.038S3u/1000。

表7 賽絡紡多元回歸分析回歸系數
表8 所示為轉杯紡雙變量皮爾遜相關性分析。表8 中,a 表示預測變量,常量,S1+2u/1 000;b表示因變量,毛羽H 值。根據分析結果篩選多元回歸分析的輸入變量為1 mm、2 mm 毛羽根數和S1+2u/1 000。轉杯紡樣本多元回歸分析結果:R20.585a,ΔR20.54,標準誤差0.02,顯著性F 變化量0.01,德賓?沃森值1.72。由此可知,多元回歸分析結果與一元回歸分析對于轉杯紡的預測效果均不理想,這可能與轉杯紡獨特的成紗方式及結構有關。轉杯紡紗線具有獨特的三層結構,中心區緊密,外層較松,表面外包纏繞纖維,表面的毛羽以圈毛羽為主,在UT6 型條干儀進行毛羽測量的過程中,轉杯紡圈毛羽因其結構相對松散而對氣流吹直毛羽進行毛羽長度測量的結果產生影響,進而導致其預測效果不理想。集聚紡、賽絡紡本質上均為傳統環錠紡,紗體結構較轉杯紡紗線更緊密,表面的毛羽以端毛羽為主,因此在毛羽測試過程中采用壓縮空氣吹直毛羽與普通光電測量的數據間關聯性相對較好。
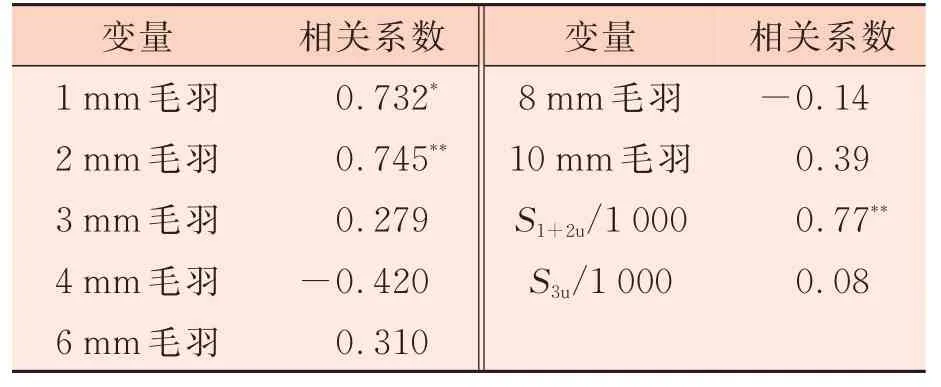
表8 轉杯紡雙變量相關性分析
3 結論
針對本研究的測試樣品和測試條件,得出的具體結論如下。
(1)利用回歸分析模型對毛羽根數值與毛羽H 值之間的相關性分析,對不同紡紗方式有選擇性,并不具備普遍適用性。
(2)一元回歸分析顯示S1+2u對毛羽H 值的預測效果優于S3u,環錠紡、集聚紡和賽絡紡S1+2u對毛羽H 值的決定系數R2均大于0.80,環錠紡、集聚紡S3u和毛羽H 值的決定系數R2均在0.70 以上,轉杯紡的一元回歸結果較差。
(3)對賽絡紡的多元回歸分析得到R2為0.955的多元回歸模型,但對于轉杯紡棉紗的預測結果較差。

