面向靜態電壓調節的無功優化電壓穩定研究?

陳 飛

（云南電力調度控制中心 昆明 650011）

1 引言

隨著電網的迅速發展和電力需求的增加，造成電壓穩定性的挑戰也越來越大［1～3］。靜態電壓是確保系統無功平衡的重要指標［4］。當系統的無功功率缺乏時，量測點的電壓就會下降；當系統的無功功率過剩時，量測點的電壓就會升高［5］。其中，電壓下降會降低區域電網的輸電能力，同時增加電力損耗，這不利于電力設備的運行［6］。同時，還可能導致系統電壓崩潰，甚至造成區域電網發生更嚴重的事故。為了保證區域電網運行安全，避免電壓失穩事故的發生，因此，有必要對如何在線監測靜態電壓穩定性進行研究。

電壓穩定性評價指標是區域電網中靜態電壓穩定性研究的重要內容，也是實現靜態電壓穩定性控制的基礎。文獻［7］中提出了L 型電壓穩定在線監測指標，由于其準確性和快速性優點，其已被廣泛應用于實際電網的電壓在線監測中。然而，現實中電網的實際電抗值大于實際電阻值，且母線電壓相位較小。文獻［8］針對靜態電壓調節，提出了L-Q 靈敏度分析方法，L-Q 靈敏度分析方法有助于定量分析不同節點之間的靜態電壓變化，但該方法需要大量的計算，并且其求解靜態電壓不穩定性的反應速度還有待提高。

針對上述問題，本文以L 型電壓穩定在線監測指標為基礎，將其局部L 指標推廣為全局L 指標，分析了不同無功功率注入對靜態電壓穩定性的影響。根據全局L 指標的可微性質，推導出一種關于無功優化的通用求解方法。該方法可以計算負載節點無功功率的注入量，并使得電網運行達到最佳穩態，確保電網運行安全，避免電壓失穩事故。

2 局部L指標的優化

根據文獻［9］提出的兩節點配電網系統靜態電壓穩定局部L 指標，本文將其局部L 指標推廣為全局L 指標，并應用于常見的多節點區域配電網系統中，并將有功功率注入節點（P 節點）和無功功率注入節點（Q 節點）組成系統中負載節點的集合，定義為αL。對于任意負載節點j(j ∈αL)，局部L指標（Lj）可描述為

其中，Sj是負載節點i 和負載節點j 的注入功率，是負載節點j 的自導納，vj是負載節點j 的電壓幅值，等于，Vi是負載節點i 的電壓矢量，和分別是負載節點i 到負載節點j 的共軛值和導納的共軛值，是負載節點j 的自導納，其數值等1 Zjj，是負載節點j 自導納的共軛值，是負載節點i 和節點j 之間互阻抗的共軛值，

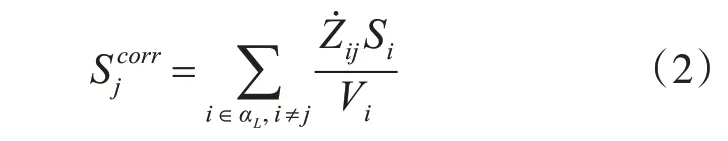
其中，Si是系統對負載節點i 的注入功率，為了保證靜態電壓的穩定性，系統中的每個負載節點j 必須滿足局部L 指標的Lj≤1［10］。則系統的全局L 指標定義如下：

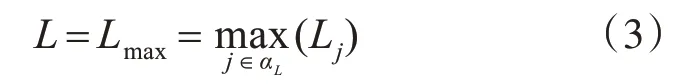
其中，L的范圍從0到1.0。L的數值越小，系統表現越穩定。當L 接近1.0 時，系統趨于臨界穩定狀態［11］。式（1）是一個運算復雜的計算公式，隨著電網規模的擴大，計算量將急劇增加。由于電抗值遠大于實際電網電阻值，且母線電壓相位較小［12］。文獻［13］在不考慮電抗和電壓相位的情況下，提出了一種簡化的L指標，為了確保系統的穩定性，L值必須小于1.0，即

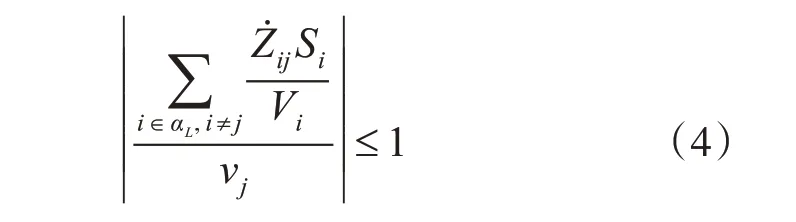
局部Lj指標與1.0 之間的差值可以用作系統的靜態電壓穩定裕度：

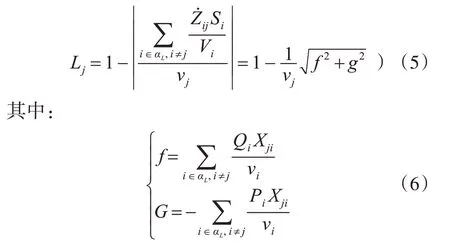
其中，Pi和Qi分別表示有功功率注入和無功功率注入。 Xji是負載節點i 和節點j 之間的電抗值，因此，式（5）可以簡化為

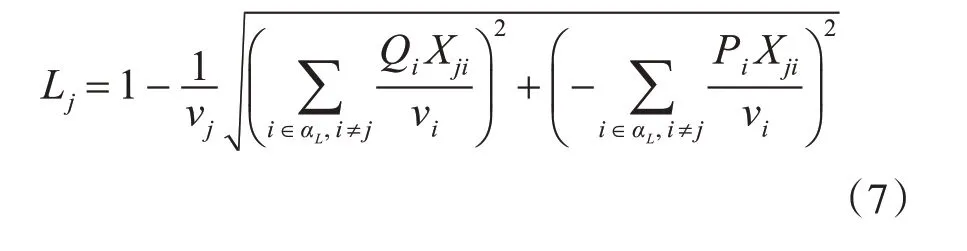
3 全局L指標的確定

當配電網需要進行無功補償時，無功功率注入的變化量設置為ΔQi，則無功功率可更新為Qi+ΔQi，并且無功功率注入與Lj的關系為

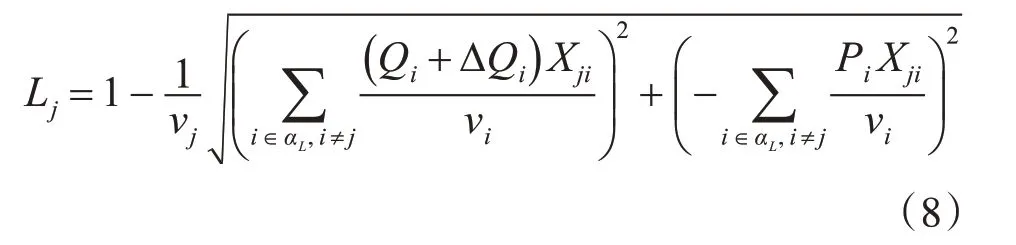
當局部Lj指標對ΔQi的一階偏導函數值設為0 時，可以得到Lj的極值。由于Lj是凸函數，因此極值是最小值。因此，當局部Lj指標為最小值時，配電網運行在最佳穩定狀態。局部Lj指標對ΔQi的一階偏導函數為

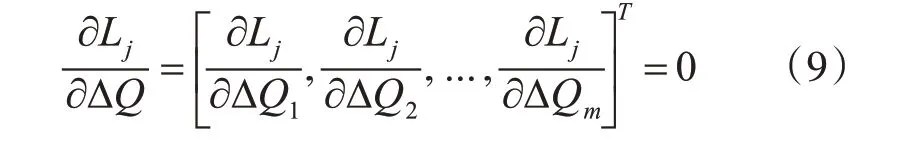
其中，m 是負載節點的數量。

由于配電網中通常存在多個節點，因此需要反復求解極值。為了簡化計算和便于理解，將每個節點對應的局部Lj指標值相加，并將總和設置為Lsum，其表達方式為

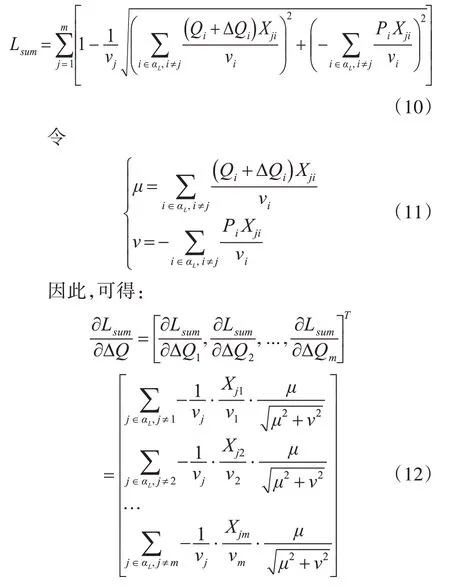
當式（12）的值等于零矢量時，可以將其轉換為矩陣形式：

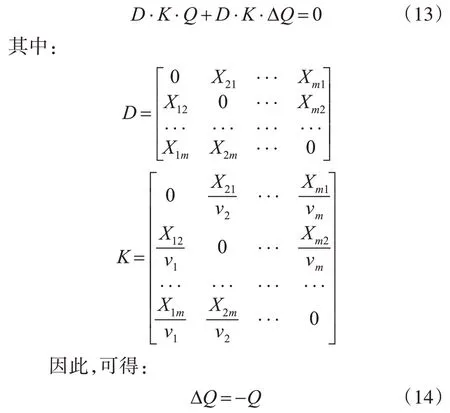
由此可見，局部無功功率注入的變化量ΔQi經過累加求和等于全局無功功率注入的變化量-Q，因此，證明了局部L指標推廣為全局L指標的合理性。

4 仿真實驗

4.1 參數設置

根據以上推導，本文在MATPOWER 平臺上對IEEE-14和IEEE-30系統分別進行測試。

測試1：IEEE-14 節點模型的基準容量為200MVA，靜態的基準電壓為35kV，整個配電網系統總負載為57.4±15.5MVA，靜態電網有16條支路，由于配電網運行是開環運行，減去原有的14，15，16三條支路，其網絡結構如圖1所示。

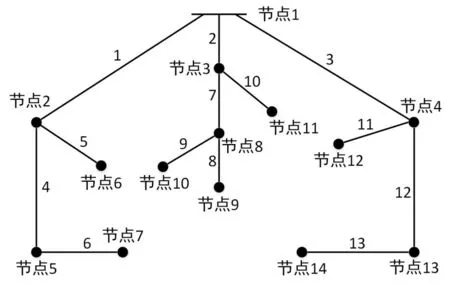
圖1 IEEE-14系統的結構

IEEE-14 系統的線路數據和節點功率分別為如表1和表2所示。

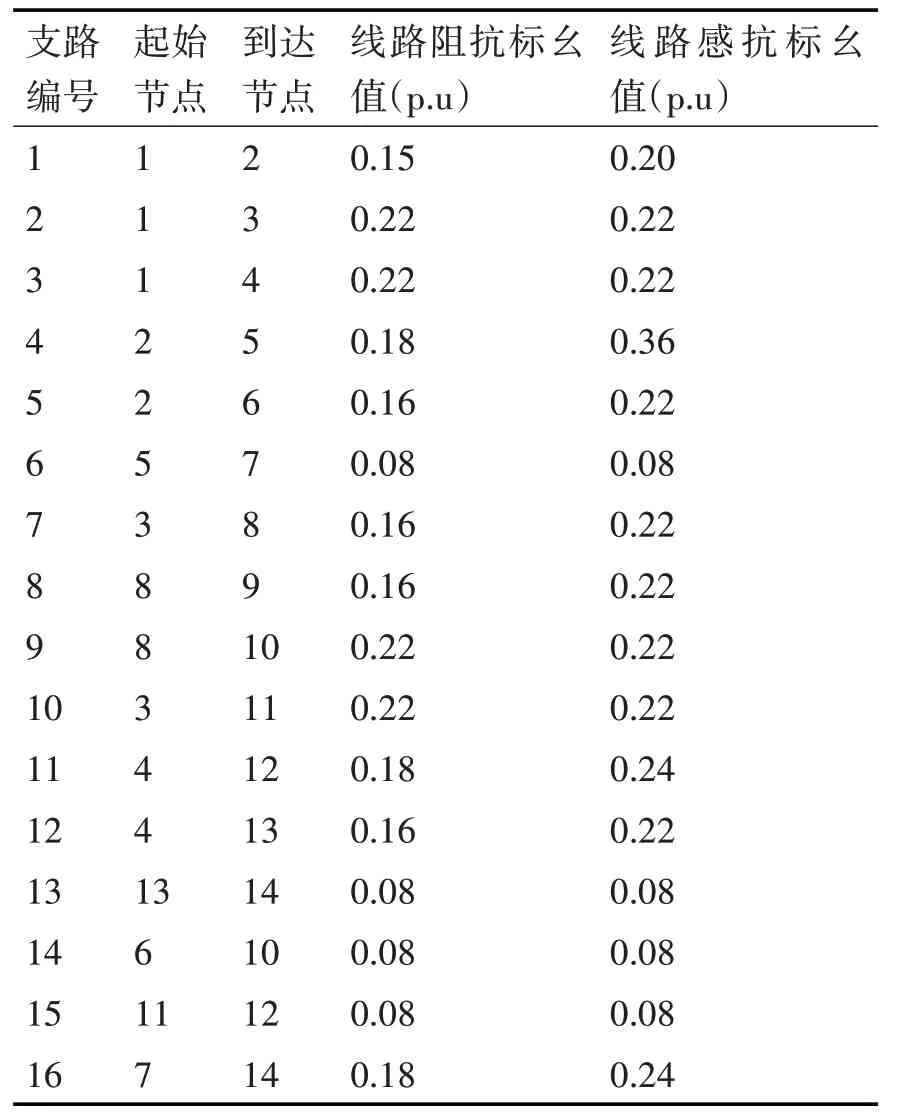
表1 IEEE-14系統的線路數據

測試2：本文所測試的IEEE-30 節點模型詳細參數詳見文獻［14］。

4.2 實驗分析

測試1：對于IEEE-14 系統，以原始負載為基準，以原始負載的1/5作為步長，負載從原始負載的0.2 倍變化到4.2 倍，如圖2 所示。其中，圖2（a）中的曲線L是沒有無功補償的全局L指標值，而Lc是具有無功補償的全局L 指標值。圖2（b）中的Ls和Lsc分別是沒有無功補償和有無功補償的所有局部Lj(j=1，2，…，m)指標值Lsum的總和。

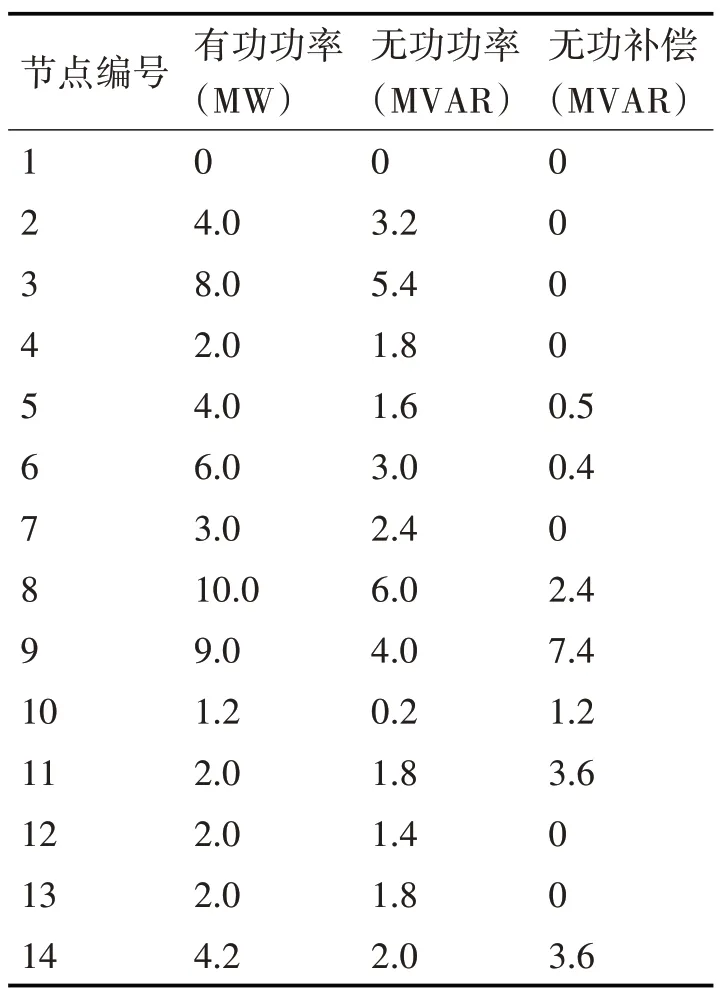
表2 IEEE-14系統的節點功率

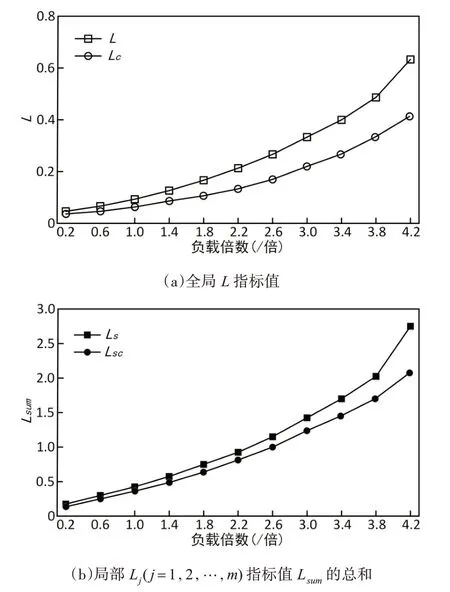
圖2 IEEE-14負載變化引起的L 指標值

由圖2（a）可見，對比曲線L 和Lc，具有無功補償的全局L 指標值Lc小于沒有無功補償的全局L指標值L，因此，本文所提出的局部L 指標推廣為全局L 指標提高靜態電壓穩定性的效果更加明顯，并且隨著負載的增大，效果越顯著，這說明所提出的方法有助于確保電網運行的安全，降低電網崩潰的風險。當負載變化到3.8 倍時，全局L 指標值接近0.5，這意味著系統處于非常敏感的狀態，即負載的輕微增加會增加靜態電壓不穩定的可能性，而Lc指標值約為0.3 時，足以避免靜態電壓的失穩。由圖2（b）可見，通過曲線L 和Lc與曲線L 和Lsc的比較，可以得出結論：兩組曲線的形狀和趨勢一致。因此，L 和Lc可以放大為Ls和Lsc，這樣也便于監測觀察。

測試2：對于IEEE-30 系統，以原始負載為基準，以原始負載的1/5作為步長，負載從原始負載的0.2 倍變化到4.2 倍，如圖3 所示。提高靜態電壓穩定性的效果與IEEE-30系統相似，負載功率裕度也得到改善。

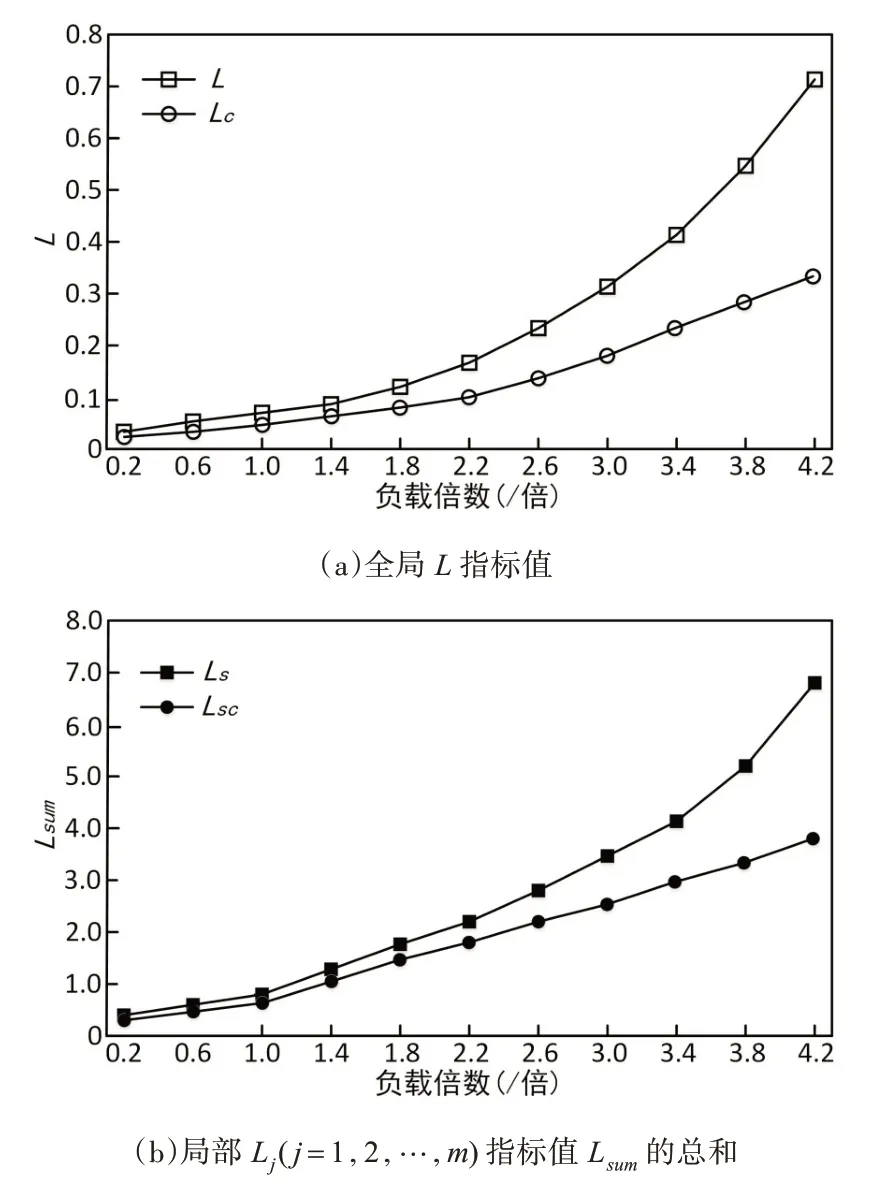
圖3 IEEE-30負載變化引起的L 指標值

由IEEE-14 和IEEE-30 系統的測試結果說明了所提方法具有普遍適用性。上述模型與實際電網之間的差異不可忽略，這使得模型的電壓降比例大于實際電網的電壓降比例。在實際電網中，電阻遠小于電抗，并且由有源負載引起的電壓降幾乎可以忽略不計。如果將所提方法應用于更接近實際電網的模型中，則結果將會更加理想。

5 結語

本文將局部L 型電壓穩定在線監測指標推廣到全局L 指標，分析了不同無功功率注入對靜態電壓穩定性的影響。根據全局L 指標的微分基本性質，推導出一種關于無功優化的通用且規范的分析算法。仿真結果表明，講該方法應用于IEEE-14和IEEE-30 系統，能夠顯著有效地提高電網的靜態電壓穩定性，降低電網崩潰的風險，且負載越大，效果越顯著。該方法具有普遍適用性，可以保證電網運行安全，避免靜態電壓失穩故障。