積分方程法在載體磁場補償中的應用?

嵇紹康 高艷麗

（海軍航空大學青島校區 青島 266041）

1 引言

利用地磁場進行導航是近幾年研究熱點［1～3］，具體有以下幾個優點［4］：1）可以完全自主且根據外部變化實時進行修正，抗干擾性和隱蔽性較好；2）與其它導航方式進行組合導航也表現較出色（與慣導組合使用，校正導航過程中的積累誤差）；3）可實現載體在地貌特征極少的地區運行；4）有實現變軌制導的可能性，提升導彈的突防性能。

地磁導航在工作過程中需要實時獲取精度較高的地磁場信息［5～6］，但是，由于載體自身存在恒磁磁場以及載體中軟磁材料被外磁場磁化所產生的磁場會嚴重干擾載體上所安裝得測量地磁場信息的傳感器［7］，如何避免“雜質”磁場的影響，獲取精準地磁場信息是目前地磁導航需要解決的一個難題。

近年來，許多學者、機構對地磁導航如何進行補償開展了許多的研究與實驗，同時提出了多種補償方案［8～13］，其中在數據擬合和補償過程中將載體運動范圍拓展到三維空間進行補償的研究相對較少，且存在一定的局限性。

本文基于積分方程法理論［14］，建立了地磁場誤差補償模型，明確了模型中各類參數的物理意義，通過參數求解得到恒磁磁場及激磁磁場系數，解決了磁場干擾補償的問題，實驗室測量結果較理想。

2 積分方程法

應用積分方程法理論，鐵磁物質受地磁場磁化在P點產生的場強為。

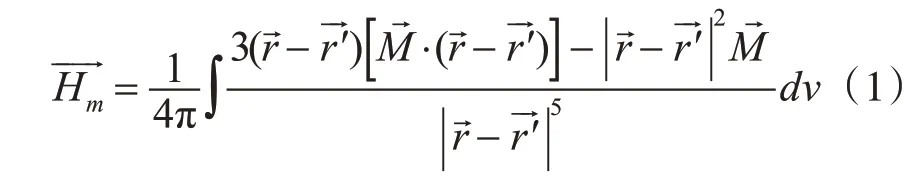
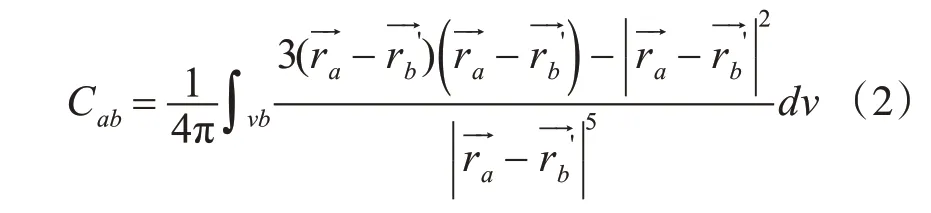
如圖1所示。

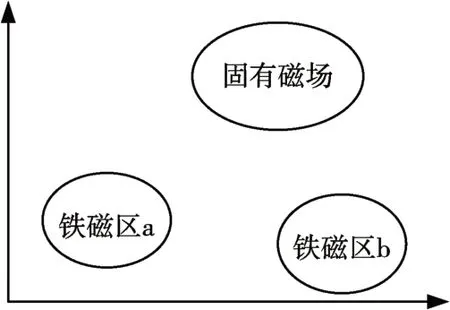
圖1 磁場源區示意圖

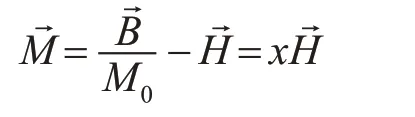
鐵磁區a受磁化而產生的磁場強度表示成：

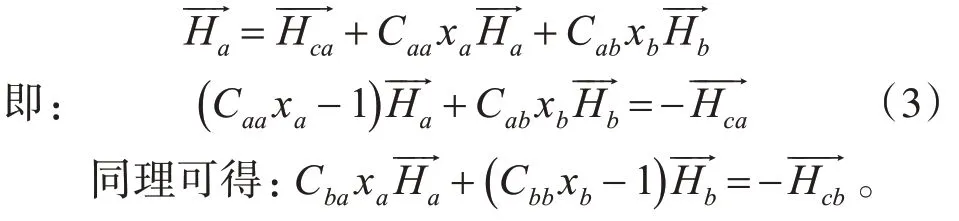
鐵磁區為飛行器殼體即內部各鐵磁物體所占的區域，將其分為n 個單元，并設各個單元的磁化率分別為x1、x2、x3、x4…xn。首先我們在這里假設各單元內的磁場強度為同一值，則對于三維場的第j個單元，有：

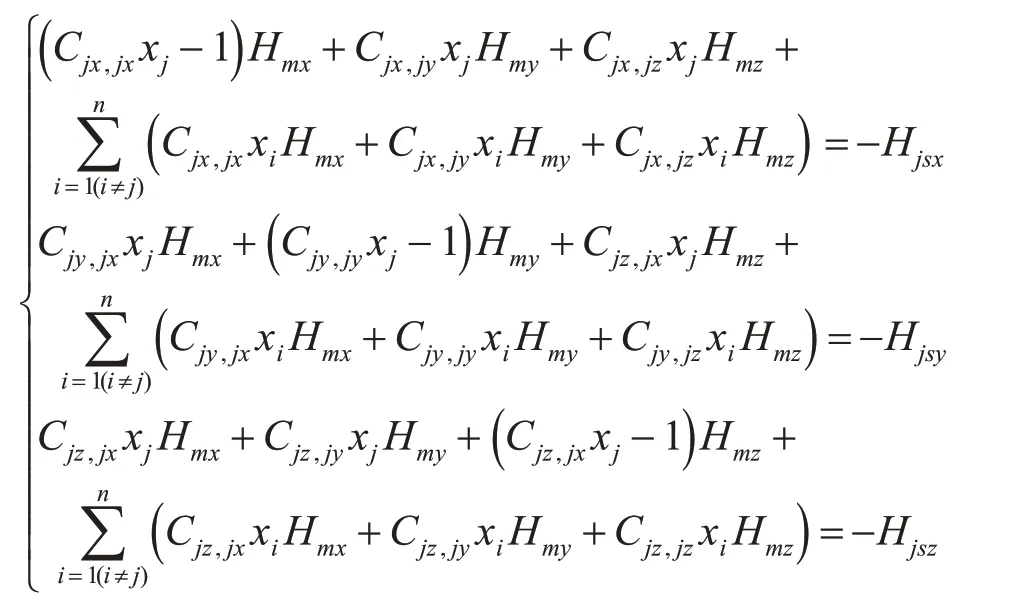
解此方程組即可求出場點a 處的磁場強度與磁化源間的關系：

由于式（4）中左邊的系數矩陣包含的干擾補償系數都是常數固定值，所以我們可以將其簡化為

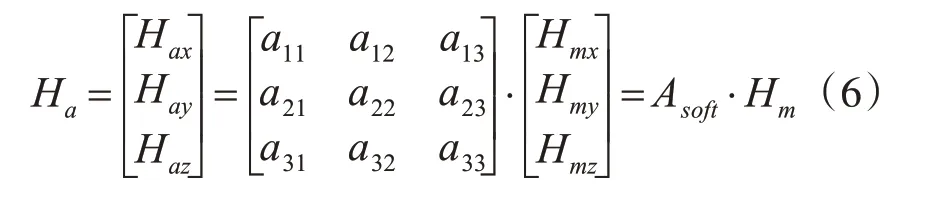
這里的Hm即載體上地磁場場強。

3 誤差模型分析

三軸磁傳感器測量值可表示為

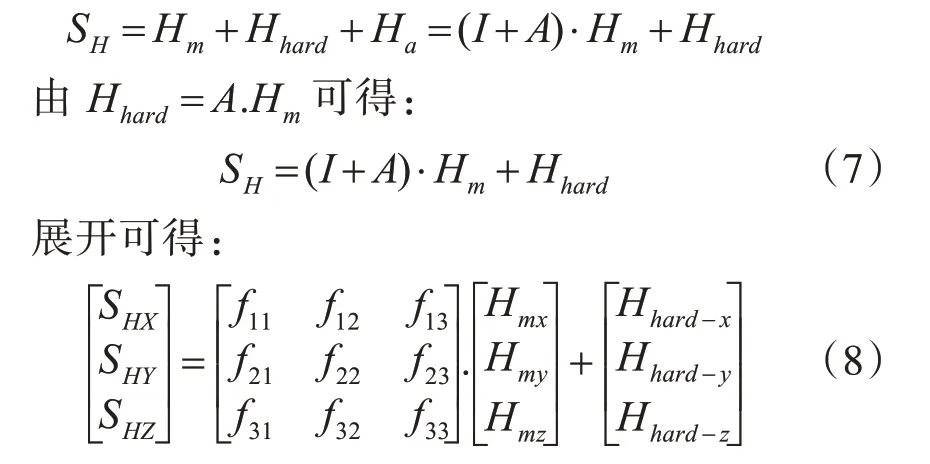
公式中包含3 個恒磁磁場固有參數和系數矩陣中的9個常系數f11、f12、f13、f21、f22、f23、f31、f32、f33，因此實驗室環境下需要至少測得四種姿態下地磁場三分量，才可解得12個補償系數值。

式（8）中含有待求誤差模型參數，可變形為

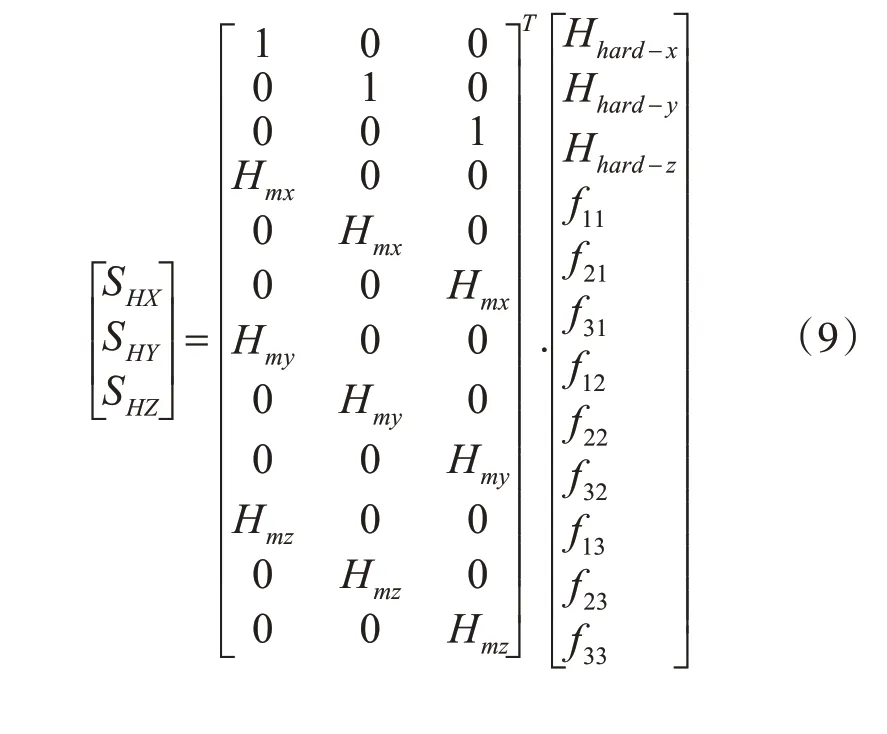
式子中含有12 個待求誤差模型參數，測量四種姿態下的磁場數據。將四種姿態下的數據合并就可采用最小二乘算法［15］求得誤差補償參數。

4 補償算法仿真分析

為了驗證該補償算法的有效性，我們在實驗室環境下，利用實驗器材無磁三軸轉臺、FVM-400 三軸磁通門磁力儀和體積為0.003 m3的矩形鐵塊進行測量試驗。首先調整轉臺三軸方位歸0，將磁力儀安裝于三軸轉臺工作臺面中心位置，記錄下轉臺不安裝鐵塊時8 種不同姿態的地磁場三分量，以此作為地磁背景場值，同時記錄下此時的轉臺姿態。然后，安裝上鐵塊作為地磁測量干擾源，調整三軸轉臺處于上述8 種對應姿態，分別記錄載體在不同姿態下磁力儀的三軸分量，將上述8 組實驗數據分別列于表1。

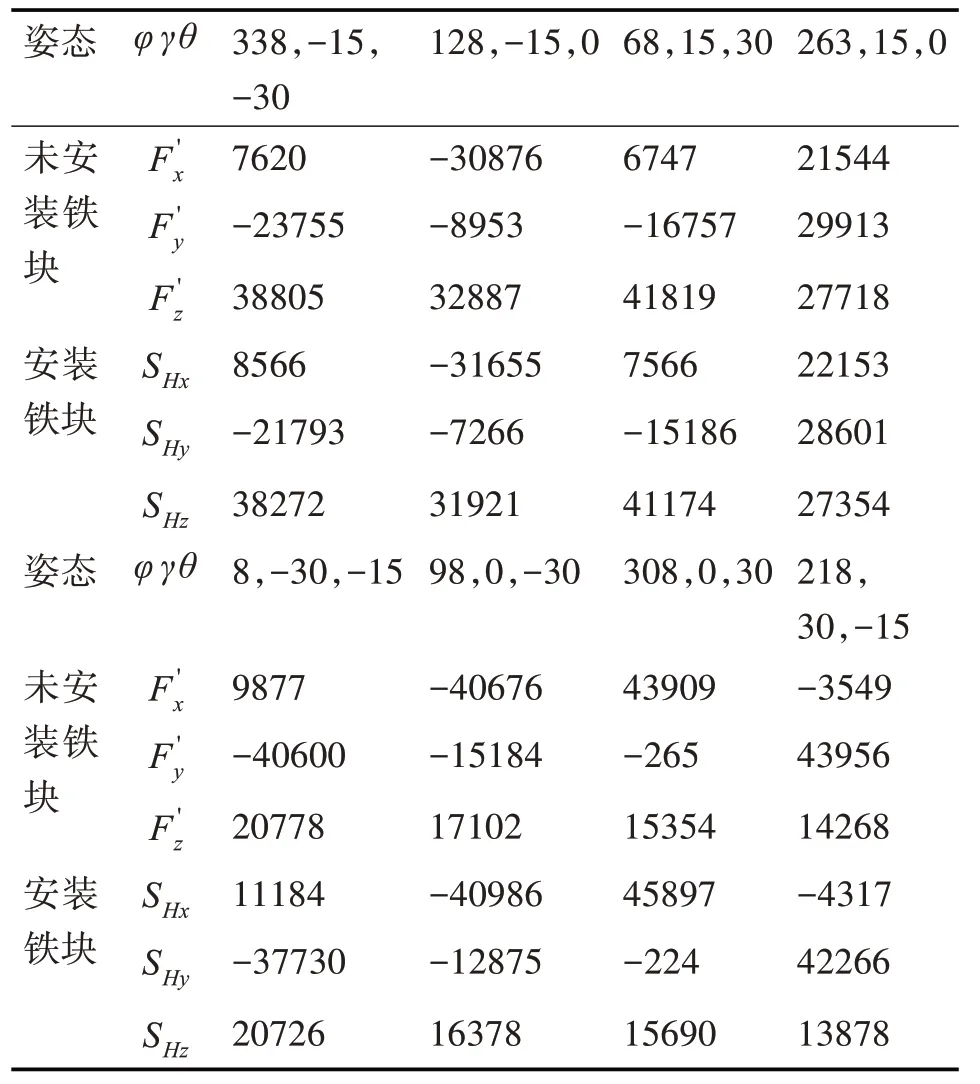
表1 實驗數據

將上述實驗數據通過Matlab進行仿真編程，計算得到式（8）中的12 補償系數，然后使轉臺處于表2 的5 種姿態下，分別測量安裝鐵塊和未安裝鐵塊時各種姿態下磁場三分量，計算5 種姿態補償后的磁場三分量。將補償前后實驗數據與實際地磁場大小作比較如表2 所示，從表中可以看出補償后的磁場測量值誤差大大降低，達到了預期的效果。

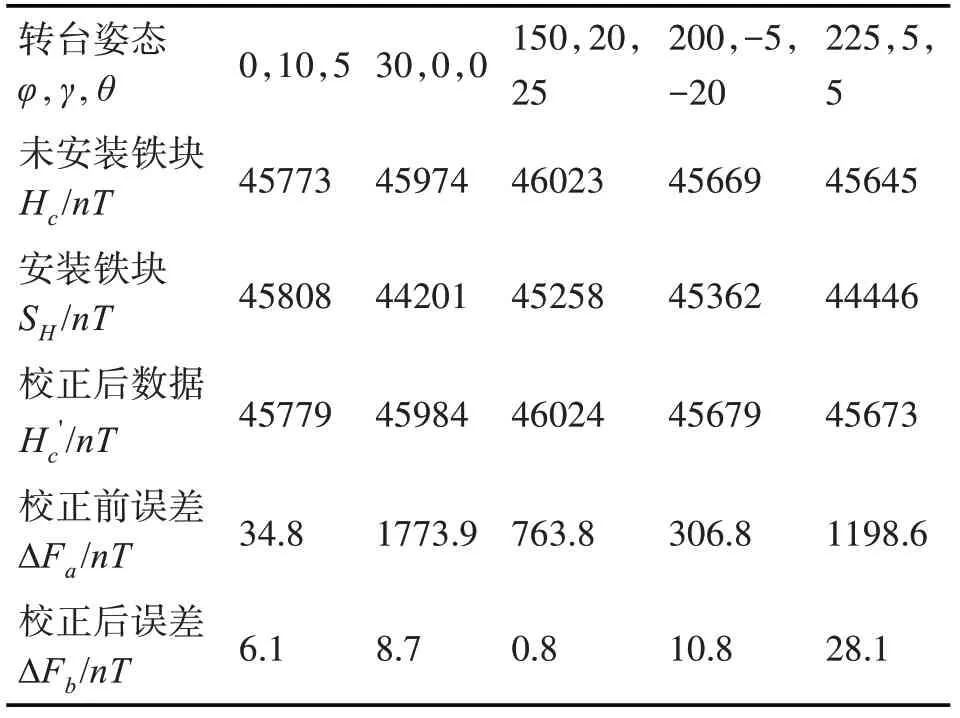
表2 誤差比較

5 結語

本文對載體自身磁場特性進行了分析了解，并著重對感應磁場的產生機理做了詳細研究，建立了地磁導航干擾誤差補償綜合模型。明確了模型中各參數的物理意義。最后運用簡單的系統辨識最小二乘估計算法求取誤差特性參數。實驗數據表明，該技術簡單易運算，較好地滿足了實際的需要。