離散廣義Markov 跳變系統在一般轉移率下的魯棒穩定性

李秀英，彭為梅

作為一類特殊的混雜系統，廣義Markov跳變系統的研究得到了廣泛的關注［1-6］.這類系統中轉移率完全已知是一種理想化的情況，因此，考慮一般轉移率即轉移率含有不確定性且部分未知情形具有更加重要的實際意義［7-8］.文獻［8］考慮了一類連續廣義Markov跳變系統在一般轉移速率下的控制器設計問題.本文研究離散廣義Markov 跳變系統在一般轉移率下的魯棒穩定性問題．

1 預備知識

考慮如下離散廣義Markov 跳變系統：其中：xk∈Rn,uk∈Rm分別是系統的狀態和控制輸入.{rk,k∈Z}是取值在有限集合S={1,2,…,N}的Markov鏈，從模態i到模態j的 轉移率定義為其中當i≠j時轉移率矩陣定義為矩陣E∈ Rn×n滿足rankE=r＜n.為表述方便，當rk=i∈S時，A(rk),B(rk)分別簡記為Ai,Bi.

本文考慮一般轉移率情形，即轉移率含有不確定性且部分未知情形.如i= 3,轉移率矩陣可設為：

其中：“？”表示轉移率矩陣中未知的轉移率.

πij與分別表示不確定轉移率的估計值和估計誤差. 令αij=πij-εij.

?i∈S, 定義其中并定義其中表示矩陣Π中第i行中序號為的 第m個已知元素表示矩陣Π 中第i行中序號 為的第N-m個未 知元素. 并令τ=

當uk= 0 時，引入如下定義：

定義1［1］①稱系統（1）是正則的，如果對任意i∈S,det(sE-Ai)不恒為零；

②稱系統（1）是因果的，如果對任意i∈S,deg(det(sE-Ai))= rankE；

③稱系統（1）是隨機穩定的，如果對x0∈Rn,r0∈S, 存在標量M(x0,r0) ＞0，使得

其中：x(t,x0,r0)表示初始條件x0,r0下系統（1）在t時的解，ε(·)表示數學期望；

④稱系統（1）是隨機容許的，如果它是正則、因果且隨機穩定的.

引理1［1］當uk= 0 時，系統（1）是隨機容許的當且僅當?i∈S，存在矩陣Pi＞0 及對稱非奇異矩陣Φ，使得下列線性矩陣不等式成立：

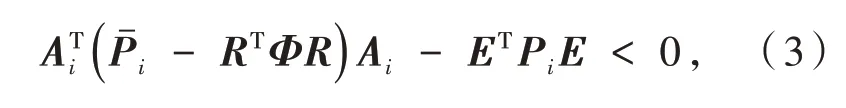
引理2［7］給定實數……